Цели работы:

а) освоение методов решения нелинейных уравнений;

б) совершенствование навыков по алгоритмизации и программированию вычислительных задач.

Постановка задачи:

Для варианта 5:

Уравнение: 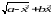=0

Метод численного решения, точность: Дихотомии, ε = 4·10^-5

Параметры: a = 1.23; b = - 3.14

Математическая часть

Вычисление каждого из действительных корней складывается из двух этапов:

1)      отделение корня, т.е. нахождение возможно малого интервала a,b, в пределах  которого находится один и только один корень x уравнения;

2)      уточнение значения корня, т.е. вычисление с заданной степенью точности.

При использовании рассматриваемых ниже методов решения уравнения к функции (x) на интервале a,b предъявляются следующие требования:

a)      функция (x) непрерывна и дважды дифференцируема (т.е. существует первая и вторая производные);

b)      первая производная '(x) непрерывна, сохраняет знак и не обращается в нуль;

c)      вторая производная "(x) непрерывна и сохраняет знак.

Пусть в уравнении (x)=0 функция (x) является непрерывной (первое требование ”a”) на интервале a,b, в котором расположен один искомый корень x. Для нахождения этого корня разделим отрезок a,b пополам точкой

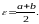
Если теперь (1) =0, то 1 и является корнем уравнения. В противном случае выбираем тот из отрезков a, 1  или 1,b, на концах которого функция (x) имеет разные знаки. В пределах этого отрезка согласно предыдущим рассуждениям лежит искомый корень. Таким образом, оказывается определенным интервал a1,b1, (где a1=a, b1=1 или a1=1, b1= b), меньший первоначального a,b и содержащий x. Повторяя подобные построения, получаем последовательность уменьшающихся интервалов a_n,b_n таких, что

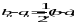(2.3)

и в каждом из которых заключен корень x. Точность вычисления корня x определяется размерами интервала a_n,b_n после n-го деления исходного интервала a,b, так как ошибка определения корня x не превышает величины b_n- a_n .

Следовательно, если ε есть заданная точность вычисления, то должно выполняться условие

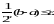(2.4)

Отсюда можно определить и необходимое число шагов половинного деления интервала a,b, если задано ε:

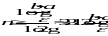
Аналитические расчеты

На рисунке 1 представлен график функции.

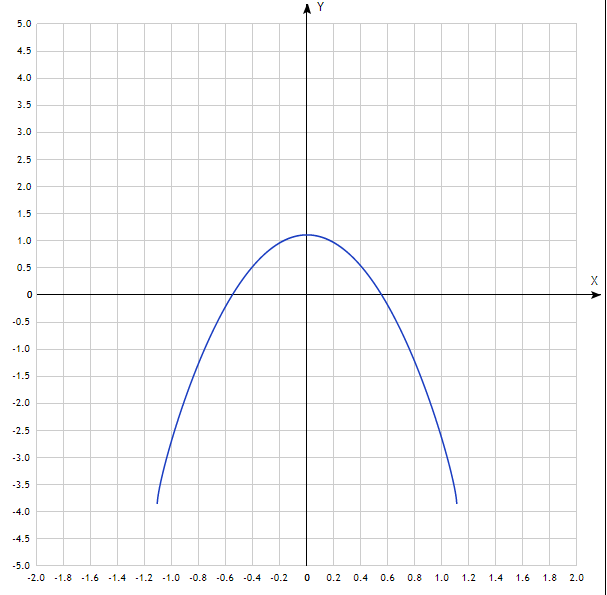
Рисунок 1 – График функции

Найдем решение с помощью онлайн калькулятора для промежутка(-1;0)

Найдем максимум функции: f(x) = (1.23-x²)¹/₂-3.14•x² Для этого целевую функцию представим в виде: F(max)=-F(min) Используем для этого Метод половинного деления (метод дихотомии).. Решение. Шаг приращения δ=0.001 Положим a₁ = a, b₁ = b. x₁=(-1+0-0.001)/2 = -0.5005 x₂=(-1+0+0.001)/2 = -0.4995 Вычислим f(x₁) = -0.20312601200401, f(x₂) = -0.20677108835715 Итерация №1. Поскольку f(x₁₁) > f(x₁₂), то a₂ = -0.4995, b₂ = b₁. x₁₁=(-0.4995+0-0.001)/2 = -0.25025 x₁₂=(-0.4995+0+0.001)/2 = -0.24925 f(x₂₁) = -0.8838, f(x₂₂) = -0.8856 Итерация №2. Поскольку f(x₂₁) > f(x₂₂), то a₃ = -0.2493, b₃ = b₂. x₂₁=(-0.24925+0-0.001)/2 = -0.125125 x₂₂=(-0.24925+0+0.001)/2 = -0.124125 f(x₃₁) = -1.0528, f(x₃₂) = -1.0537 Итерация №3. Поскольку f(x₃₁) > f(x₃₂), то a₄ = -0.1241, b₄ = b₃. x₃₁=(-0.124125+0-0.001)/2 = -0.0625625 x₃₂=(-0.124125+0+0.001)/2 = -0.0615625 f(x₄₁) = -1.095, f(x₄₂) = -1.0954 Итерация №4. Поскольку f(x₄₁) > f(x₄₂), то a₅ = -0.06156, b₅ = b₄. x₄₁=(-0.0615625+0-0.001)/2 = -0.03128125 x₄₂=(-0.0615625+0+0.001)/2 = -0.03028125 f(x₅₁) = -1.1055, f(x₅₂) = -1.1058 Остальные расчеты сведем в таблицу.

N	an	bn	bn-an	xn1	xn2	F(xn1)	F(xn2)	εn
1	-1	0	-0.5	-0.5005	-0.4995	-0.2031	-0.2068	0.2503
2	-0.4995	0	0.4995	-0.2503	-0.2493	-0.8838	-0.8856	0.06281
3	-0.2493	0	0.2493	-0.1251	-0.1241	-1.0528	-1.0537	0.01602
4	-0.1241	0	0.1241	-0.06256	-0.06156	-1.095	-1.0954	0.00435
5	-0.06156	0	0.06156	-0.03128	-0.03028	-1.1055	-1.1058	0.00145
6	-0.03028	0	0.03028	-0.01564	-0.01464	-1.1082	-1.1083	0.000729
7	-0.01464	0	0.01464	-0.00782	-0.00682	-1.1088	-1.1089	0.000553
8	-0.00682	0	0.00682	-0.00391	-0.00291	-1.109	-1.109	0.000511
9	-0.00291	0	0.00291	-0.00196	-0.000955	-1.109	-1.1091	0.000502
10	-0.000955	0	0.000955	-0.000978	2.2E-5	-1.1091	-1.1091	0.0005

|-1.1090460479371-(-1.1090528317742)|≤0.0004 Находим x как середину интервала [a,b]: x=(0-0.955078125)/2 = -0.55334590625

Ответ: x= -0.55334590625; F(x)=-1.1090528317742

Для интервала (0;1):

Найдем максимум функции: f(x) = (1.23-x²)¹/₂-3.14•x² Для этого целевую функцию представим в виде: F(max)=-F(min) Используем для этого Метод половинного деления (метод дихотомии).. Решение. Шаг приращения δ=0.001 Положим a₁ = a, b₁ = b. x₁=(0+1-0.001)/2 = 0.4995 x₂=(0+1+0.001)/2 = 0.5005 Вычислим f(x₁) = -0.20677108835715, f(x₂) = -0.20312601200401 Итерация №1. Поскольку f(x₁₁) ≤ f(x₁₂), то b₂ = 0.4995, a₂ = a₁. x₁₁=(0+0.4995-0.001)/2 = 0.24925 x₁₂=(0+0.4995+0.001)/2 = 0.25025 f(x₂₁) = -0.8856, f(x₂₂) = -0.8838 Итерация №2. Поскольку f(x₂₁) ≤ f(x₂₂), то b₃ = 0.2493, a₃ = a₂. x₂₁=(0+0.24925-0.001)/2 = 0.124125 x₂₂=(0+0.24925+0.001)/2 = 0.125125 f(x₃₁) = -1.0537, f(x₃₂) = -1.0528 Итерация №3. Поскольку f(x₃₁) ≤ f(x₃₂), то b₄ = 0.1241, a₄ = a₃. x₃₁=(0+0.124125-0.001)/2 = 0.0615625 x₃₂=(0+0.124125+0.001)/2 = 0.0625625 f(x₄₁) = -1.0954, f(x₄₂) = -1.095 Итерация №4. Поскольку f(x₄₁) ≤ f(x₄₂), то b₅ = 0.06156, a₅ = a₄. x₄₁=(0+0.0615625-0.001)/2 = 0.03028125 x₄₂=(0+0.0615625+0.001)/2 = 0.03128125 f(x₅₁) = -1.1058, f(x₅₂) = -1.1055 Остальные расчеты сведем в таблицу.

N	an	bn	bn-an	xn1	xn2	F(xn1)	F(xn2)	εn
1	0	1	0.5	0.4995	0.5005	-0.2068	-0.2031	0.2503
2	0	0.4995	0.4995	0.2493	0.2503	-0.8856	-0.8838	0.06281
3	0	0.2493	0.2493	0.1241	0.1251	-1.0537	-1.0528	0.01602
4	0	0.1241	0.1241	0.06156	0.06256	-1.0954	-1.095	0.00435
5	0	0.06156	0.06156	0.03028	0.03128	-1.1058	-1.1055	0.00145
6	0	0.03028	0.03028	0.01464	0.01564	-1.1083	-1.1082	0.000729
7	0	0.01464	0.01464	0.00682	0.00782	-1.1089	-1.1088	0.000553
8	0	0.00682	0.00682	0.00291	0.00391	-1.109	-1.109	0.000511
9	0	0.00291	0.00291	0.000955	0.00196	-1.1091	-1.109	0.000502
10	0	0.000955	0.000955	-2.2E-5	0.000978	-1.1091	-1.1091	0.0005

|-1.1090460479371-(-1.1090528317742)|≤0.0004 Находим x как середину интервала [a,b]: x=(0.955078125+0)/2 = 0.55334590625 Ответ: x= 0.55334590625; F(x)=-1.1090528317742

Схема алгоритма решения задачи

На рисунках 2, 3 изображена блок схема алгоритма решения задачи

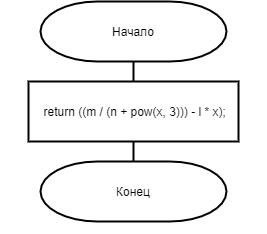
Рисунок 2 - блок-схема функции

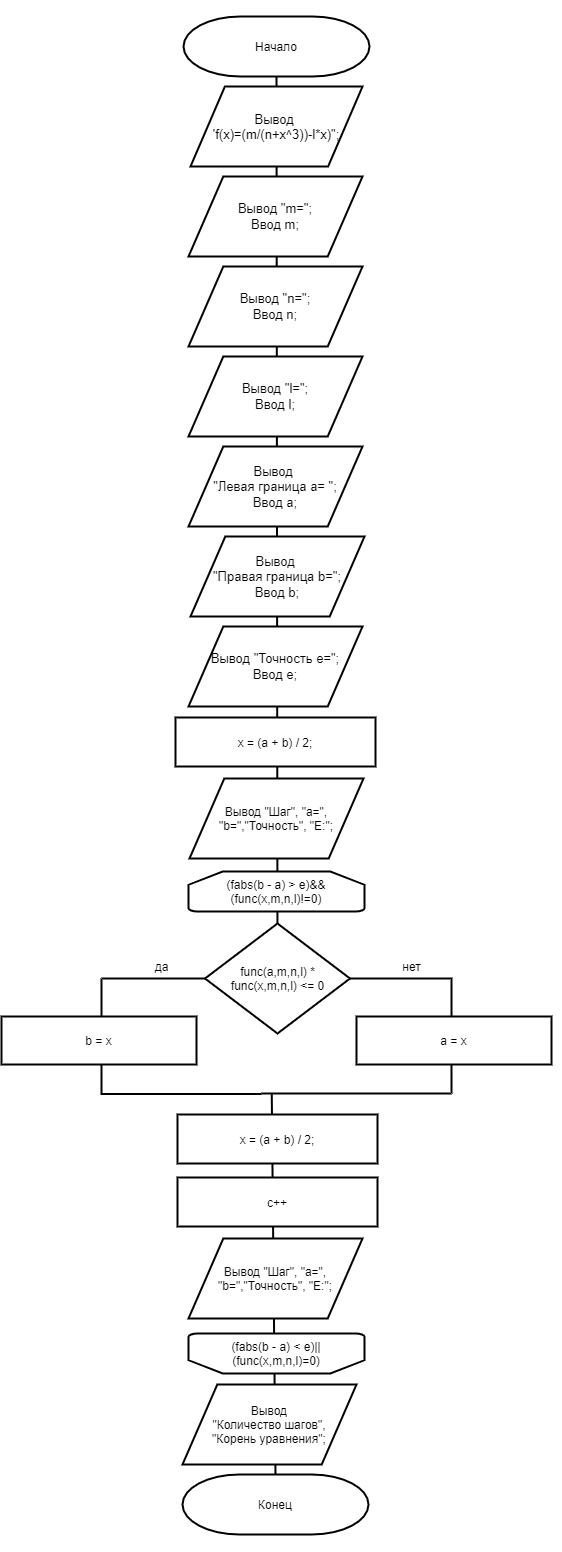
Рисунок 3 - блок-схема main

Текст программы на языке C/C++

#include <iostream>

#include <math.h>

#include <conio.h>

using namespace std;

double func(double x) // функция

{

return (sqrt(1.23-x*x) - 3.14 * x * x);

}

int main()

{

setlocale(LC_ALL, "ru");

double a, b, e, x;

int c = 1;

cout << "f(x)=((1.23-x^2)^1/2 - 3.14 * x^2)\n";

cout << "Левая граница a=";

cin >> a;

cout << "Правая граница b=";

cin >> b;

cout << "Точность e=";

cin >> e;

x = (a + b) / 2;

cout << "Шаг 1" << endl << "E: " << x << endl << "a= " << a << endl << "b= " << b << endl << "Точность: " << fabs(b - a) << endl;

while (fabs(b - a) > e)

{

if (func(a) * func(x) <= 0) b = x;

else a = x;

x = (a + b) / 2;

c++;

cout << "\nШаг № " << c << endl << "E: " << x << endl << "a= " << a << endl << "b= " << b << endl << "Точность: " << fabs(b - a) << endl;

}

cout << "\nКоличество шагов: " << c << "\nКорень уравнения: " << x << endl;

system("pause");

return 0;

}