lect10_m2_vm1_vt_aig_230100.62_niy06

Лекция 10

Глава 8

Системы линейных алгебраических уравнений

Первоначальные понятия. Метод Гаусса

8.1. Метод Гаусса

Пусть дана система уравнений первой степени (линейных) с неизвестными. Неизвестные обозначим , уравнения будем считать пронумерованными: первое, второе,…, -е. Коэффициент из -го уравнения при неизвестном обозначим , свободный член - .

Система запишется в следующем виде:

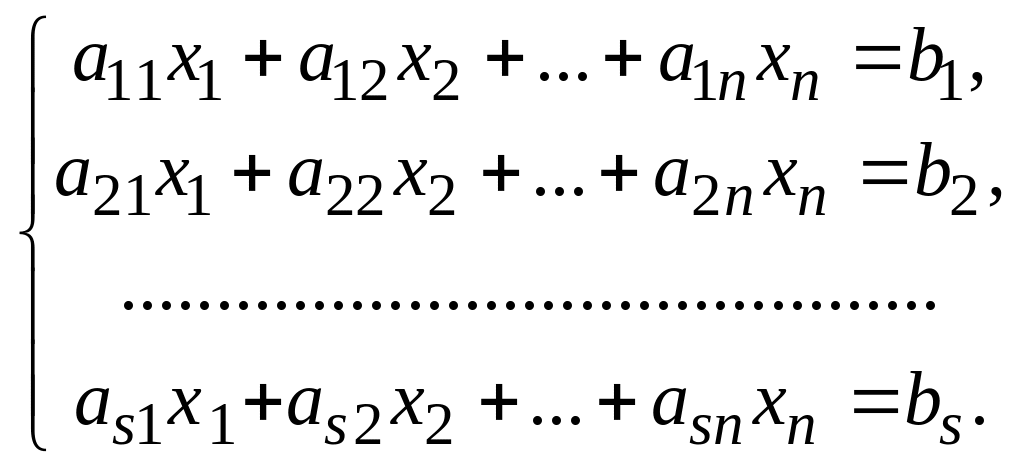(8.1)

Определение 1. Решением системы линейных уравнений (8.1) называется такой набор чисел , что каждое из уравнений (8.1) обращается в тождество после замены неизвестных числами , .

Определение 2. Система (8.1) называется несовместной, если она не имеет решений, и совместной, если она имеет решения.

Определение 3. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если решений более одного.

Определение 4. Две системы линейных уравнений называются эквивалентными, если они обе несовместны, или обе совместны и имеют одни и те же решения.

Наиболее удобным для практического разыскания решений системы (8.1) является метод последовательного исключения неизвестных, или метод Гаусса.

Выполним следующие преобразования системы: обе части одного уравнения умножим на некоторое число и прибавим к обеим частям другого уравнения. Покажем, что мы придем к эквивалентной системе.

Пусть обе части первого уравнения системы (8.1), умноженные на число , прибавляются к обеим частям второго уравнения. Получаем систему

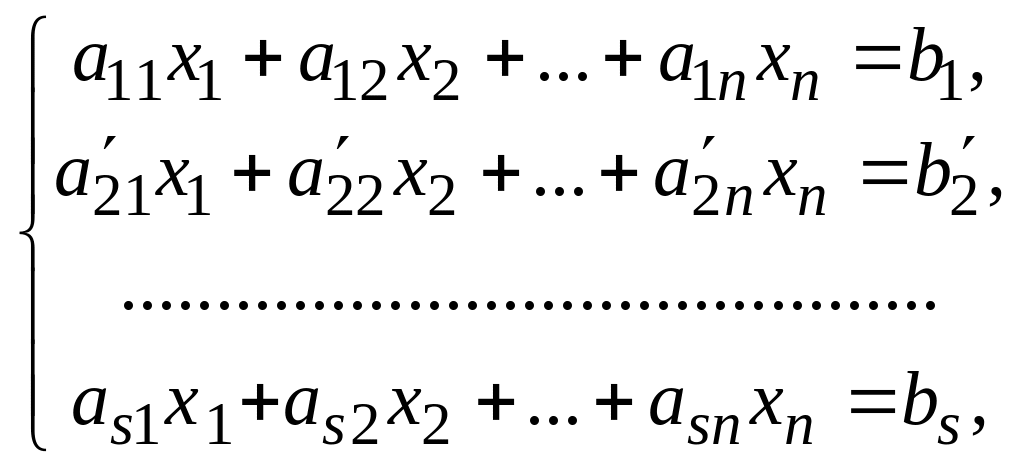(8.2)

где , …, , .

Пусть - решение системы (8.1). Это означает, что выполняются тождества:

(8.3)

Равенства (8.3) означают, что набор чисел удовлетворяет первому, третьему,…, -му уравнению системы (8.2). Удовлетворяют эти числа и второму уравнению, так как, если к обеим частям второго тождества в системе (8.3) прибавить обе части первого, умноженные на , получим

.

Таким образом, всякое решение системы (8.1) является решением системы (8.2).

Справедливо обратное. Пусть - решение системы (8.2), тогда

.

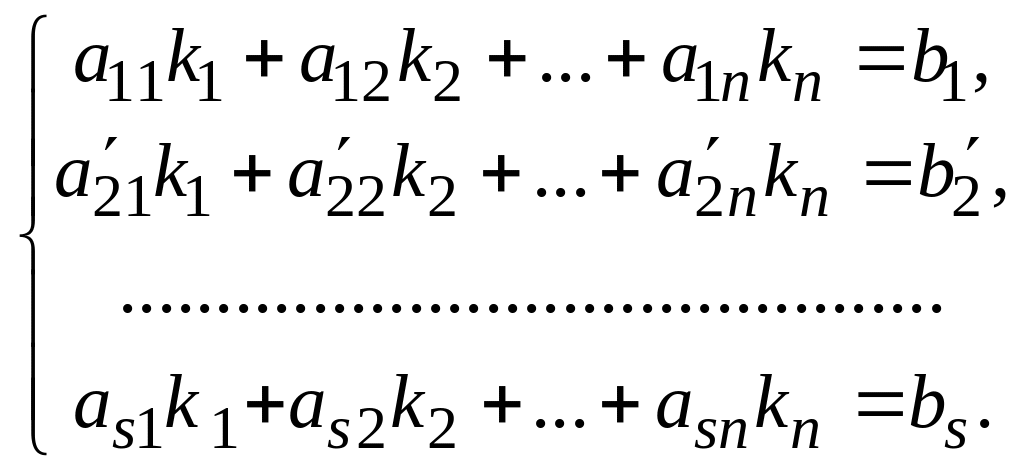(8.4)

Тождества (8.4) означают, что набор чисел удовлетворяет первому, третьему,…, -му уравнению системы (8.1). Если к обеим частям второго тождества в (8.4) прибавить обе части первого, умноженные на , получим

,

то есть удовлетворяют также второму уравнению в (8.1), и всякое решение системы (8.2) является решением системы (8.1). Системы (8.1) и (8.2) в соответствии с определением 4 эквивалентны.

Перейдем к изложению метода Гаусса.

Дана система (8.1). Пусть (если это не так, возьмем в качестве первого любое другое уравнение с коэффициентом при , отличным от нуля, и перенумеруем уравнения; хотя бы одно такое уравнение найдется, иначе просто отсутствовал бы).

Обе части первого уравнения, умноженные на , прибавим к обеим частям второго уравнения, умноженные на , - к обеим частям третьего и т.д., умноженные на - к обеим частям -го уравнения. Придем к новой системе:

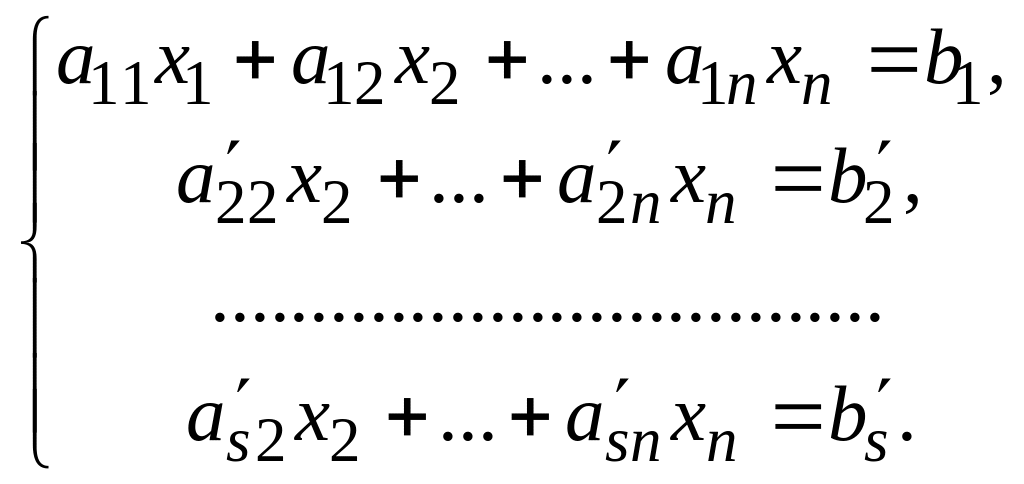(8.5)

Система (8.5) эквивалентна системе (8.1).

Первое неизвестное исключили из всех уравнений системы, начиная со второго.

Уже после первого шага может встретиться уравнение вида

, . (8.6)

Если , этому уравнению удовлетворяет любой набор чисел . В этом случае уравнение будем отбрасывать. Если , уравнению (8.6) не удовлетворяет никакой набор чисел , и система, содержащая такое уравнение (8.6), несовместна, следовательно, несовместна и эквивалентная ей система (8.1). В этом случае преобразования по методу Гаусса будем прерывать.

Итак, имеем систему (8.5). Среди коэффициентов , , , есть отличные от нуля (иначе либо система несовместна, либо уравнения можно отбросить). Пусть для определенности (если , но отличен от нуля коэффициент при в другом уравнении, можно перенумеровать уравнения, если , можно перенумеровать неизвестные). Обе части второго уравнения, умноженные на , прибавим к обеим частям третьего уравнения и т.д., обе части второго уравнения, умноженные на , - к обеим частям -го уравнения. Этим исключим неизвестное из всех уравнений, кроме первого и второго, и придем к системе

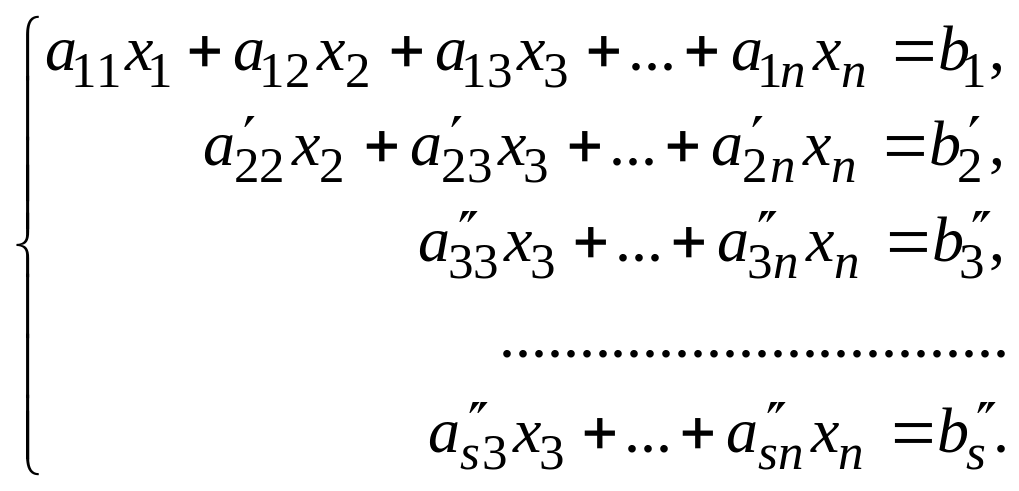
Аналогичным образом продолжим процесс исключения неизвестных.

Если после нескольких шагов получим уравнение вида (8.6), в котором , можно сделать вывод о несовместности системы. Если же такое уравнение не встретится, придем к системе

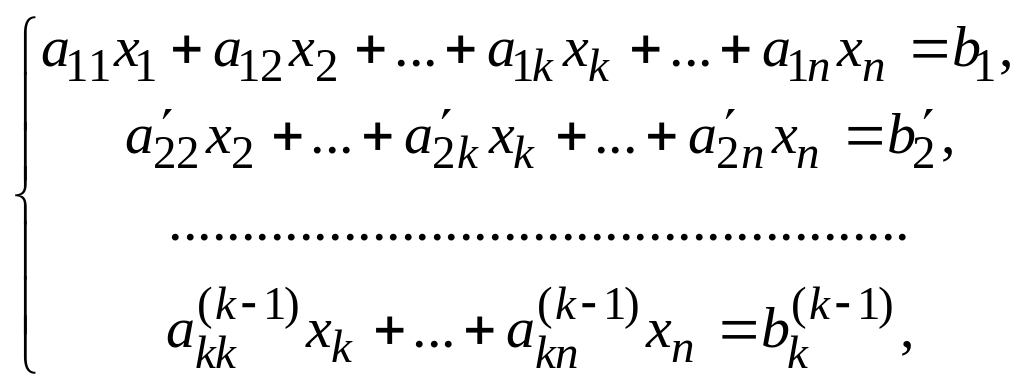(8.7)

эквивалентной системе (8.1). Здесь , , …, , .

При система (8.7) имеет вид

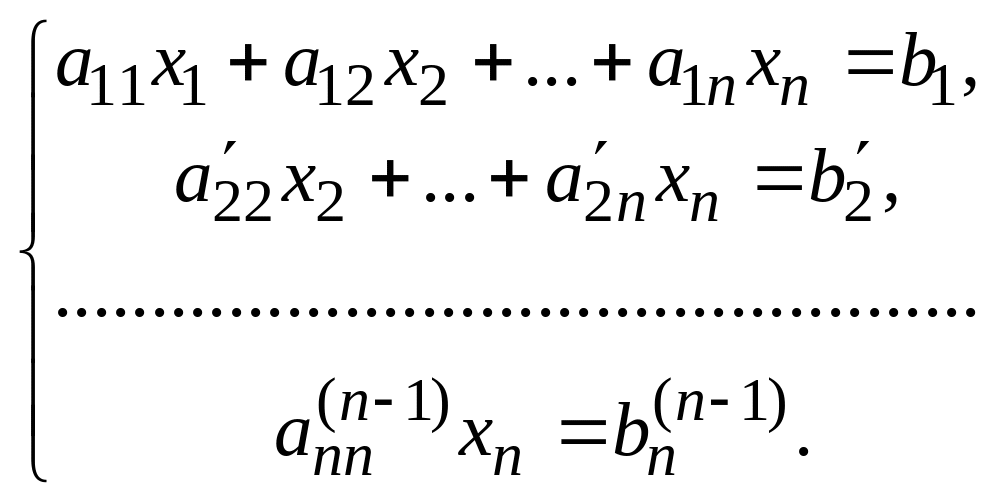(8.8)

Из последнего уравнения найдем значение ( ), подставим в -е, найдем ( ) и т.д. до первого уравнения, из которого определится . Система (8.8) в этом случае имеет единственное решение и эквивалентная ей система (8.1) является определенной.

При в последнем уравнении системы (8.7) присвоим неизвестным произвольные числовые значения:

.

Из последнего, -го, уравнения системы (8.7) найдем ( ), подставим в -е уравнение, найдем и т.д., двигаясь снизу вверх по системе (8.7), найдем вполне определенные значения . Так как значения для неизвестных можно выбрать бесчисленным множеством способов, система (8.7) в случае будет неопределенной.

Итак, метод Гаусса применим к любой системе линейных уравнений. Если в процессе преобразований встретится уравнение, в котором все коэффициенты при неизвестных равны нулю, а свободный член отличен от нуля, система несовместна. Если такое уравнение не встретится, система совместна. Она является определенной, если приводится к треугольному виду (8.8), и неопределенной, если приводится к трапецеидальному виду (8.7).

Пример. Решить систему методом Гаусса:

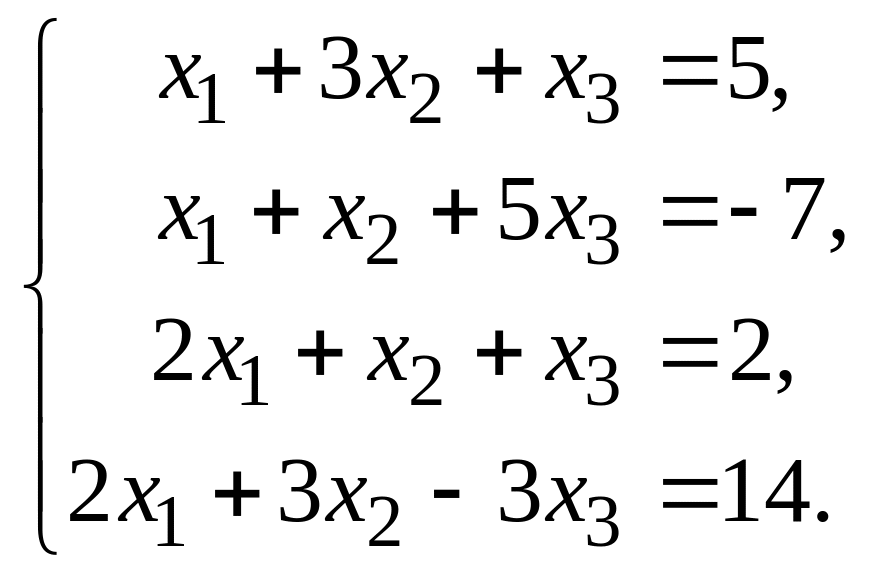
Решение. Исключаем неизвестное . Первое уравнение, умноженное на , прибавляем ко второму, умноженное на , – к третьему и четвертому, получаем

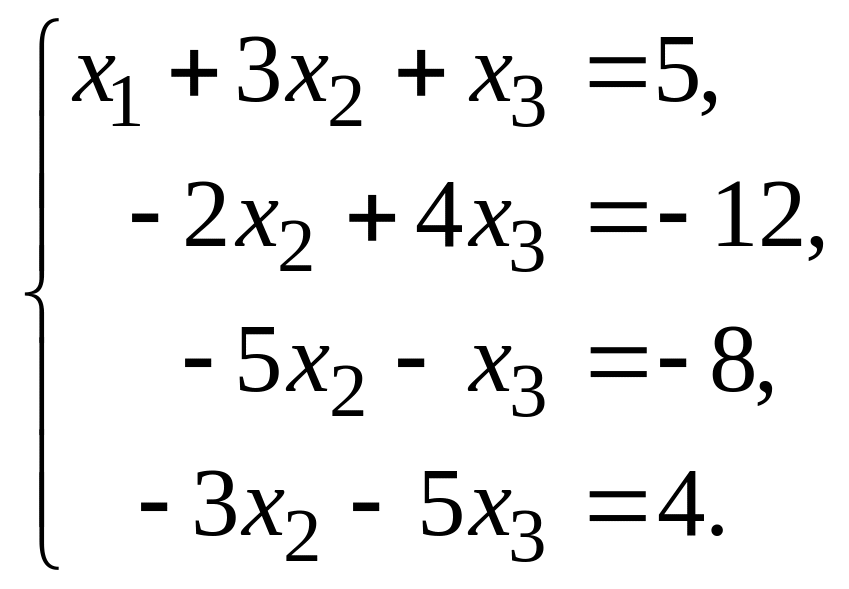
Обе части второго уравнения умножаем на :

.

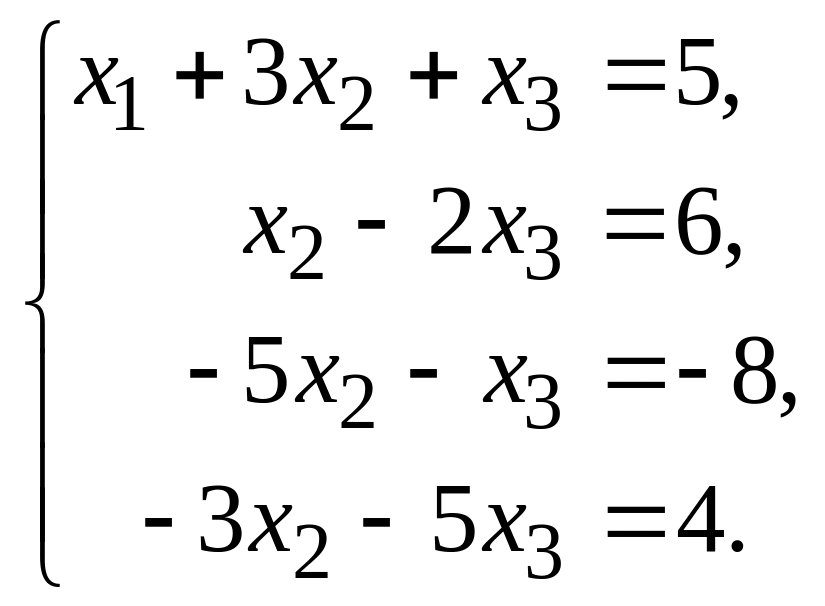Второе уравнение, умноженное на , прибавляем к третьему, умноженное на , - к четвертому, получаем:

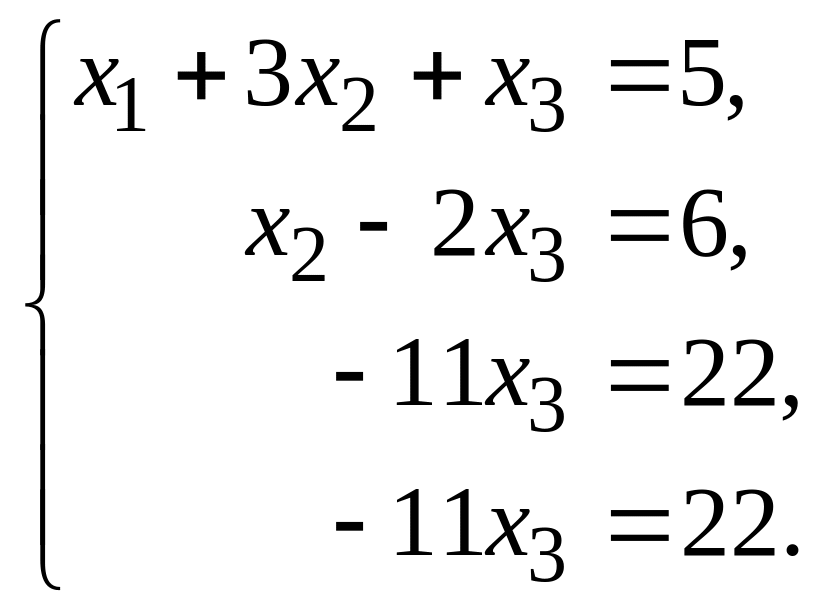
Обе части третьего уравнения, умноженные на , прибавляем к четвертому уравнению, получаем

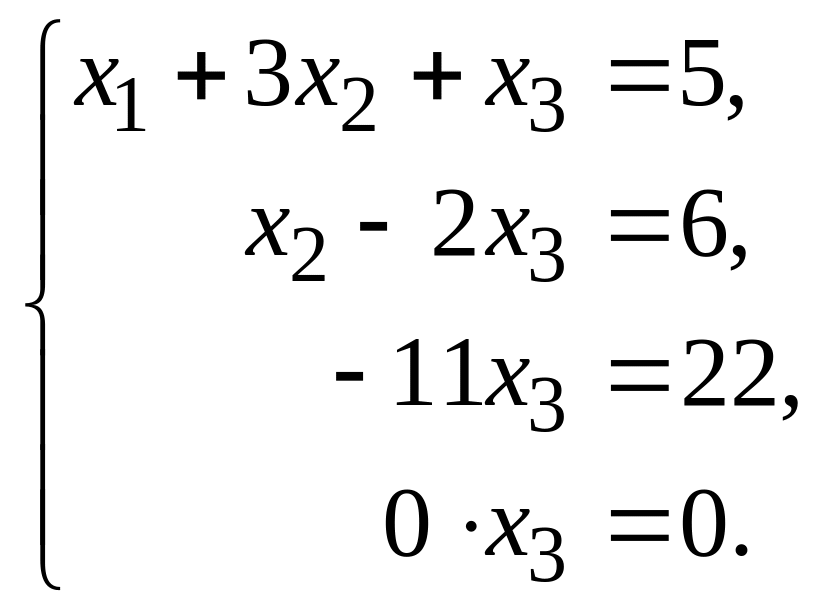
Последнее уравнение отбрасываем, из третьего уравнения находим , подставляем во второе и находим . Затем и подставляем в первое уравнение , откуда .

Итак, , , - решение исходной системы, найденное методом Гаусса.

Упражнения. Решить методом Гаусса следующие системы уравнений:

1.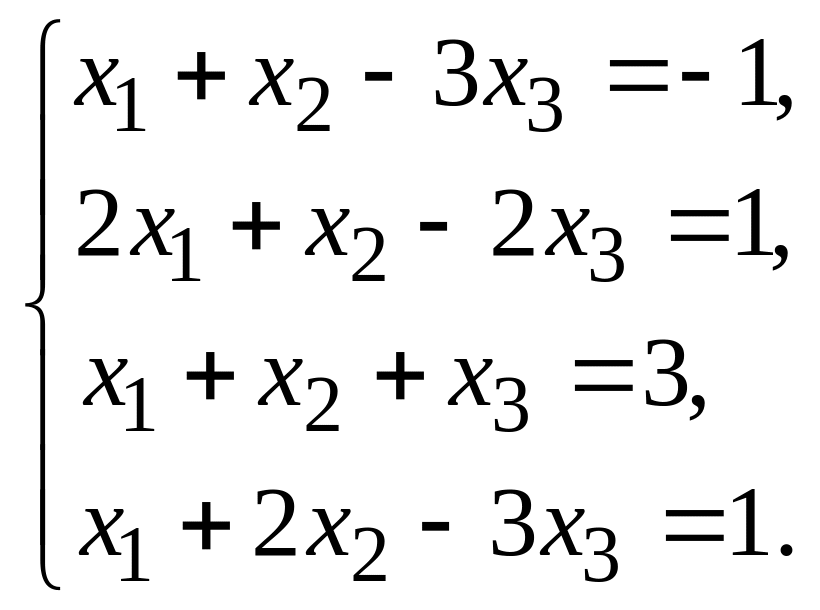 2.

3.

114