Лекц / pdf / Общий

С учетом перечисленных условий рассматриваемого процесса дросселирования, уравнение первого начала термодинамики для потока по балансу рабочего тела

dQ* + dQ** = dH + dW * + dW **

примет вид

H2 - H1 = 0 или H = idem

Это значит, что рассматриваемый процесс дросселирования

является процессом изоэнтальпийным: энтальпия рабочего

.

тела до дросселя численно равна энтальпии рабочего тела после дросселя. При течении внутри дросселя энтальпия газа или пара меняется.

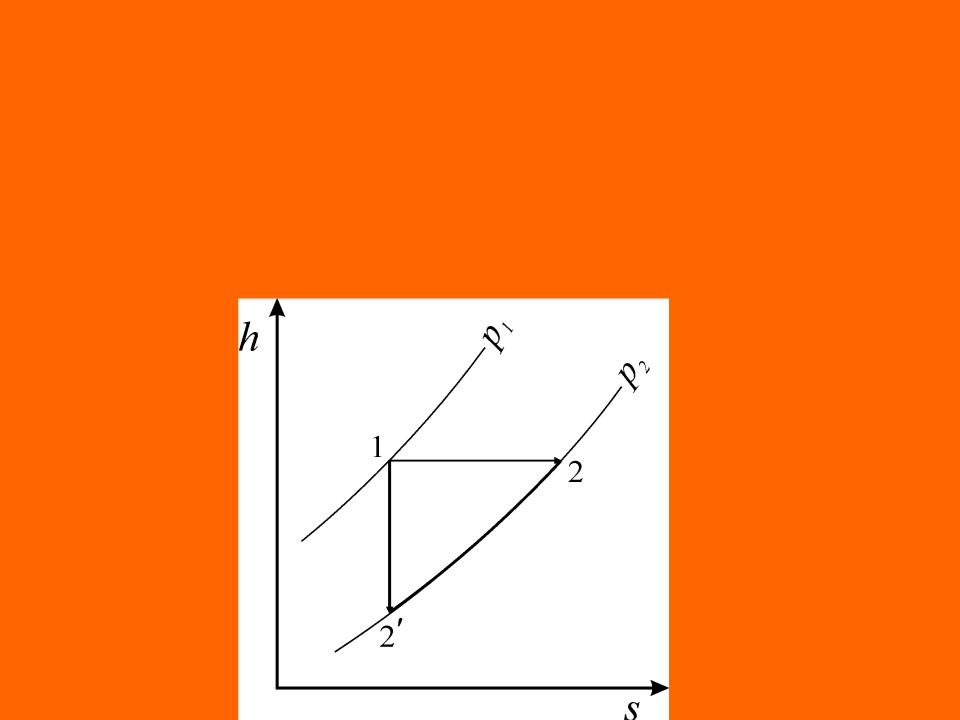
Если рассматривать в качестве местного сопротивления

сужение канала, в суженном сечении поток ускоряется, кинетическая энергия увеличивается и энтальпия рабочего тела уменьшается (процесс 1 - 2'). После дросселя сечение потока вновь возрастает, поток тормозится, кинетическая энергия уменьшается, а энтальпия увеличивается до прежнего значения (процесс 2' - 2).

Коэффициент Джоуля – Томсона определяется из следующего уравнения, выведенного из математических выражений первого начала термодинамики и второго начала

Знак дифференциального дроссель–эффекта (коэффициента Джоуля – Томсона) определяется из анализа уравнения. В зависимости от характера изменения температуры T, имеют место три вида дроссель–эффекта (процесс дросселирования всегда происходит с падением давления dp<0):

1.Дроссель–эффект положительный (Dh > 0), в этом случае процесс дросселирования сопровождается снижением температуры рабочего тела (dT<0);

2.Дроссель–эффект отрицательный (Dh < 0), в этом случае процесс дросселирования сопровождается повышением температуры рабочего тела (dT>0);

3.Дроссель–эффект равен нулю (Dh = 0), если в процессе дросселирования температура рабочего тела не изменяется. Нулевой дроссель-эффект наблюдается при дросселировании идеального газа.

Как показывает опыт, для одного и того же вещества в зависимости от значений параметров состояния коэффициент Джоуля – Томсона Dh может иметь положительные, отрицательные значения, а также быть равным нулю.

Состояние газа или жидкости, которому соответствует условие Dh = 0, называется точкой инверсий. Геометрическое место точек инверсии на диаграмме состояния данного вещества называется кривой инверсии.

Кривая инверсии описывается уравнением

Для каждого вещества в диаграмме р - v имеется своя кривая инверсии. Закон соответственных состояний позволяет построить обобщенные кривые инверсии для групп термодинамически подобных веществ. Для природных газов инверсионная диаграмма приведена на графике в виде π = f(τ)

Пары и парообразование

Процесс парообразования. Основные определения

Процесс парообразования и методика определения основных характеристик процесса парообразования для всех жидкостей практически аналогичны, что дает возможность рассматривать процесс парообразования на примере воды, как одного из наиболее распространенных веществ в природе.

Рассмотрим изобарный процесс парообразования 1 кг воды в координатах р – v

Процесс кипения протекает на участке а'- а" при постоянном давлении р1 и постоянной температуре ts1. В точке (а") вода полностью испаряется. Пар в этом состоянии называется сухим насыщенным. На участке (а'-а") вода находится в двух фазах и состоит из смеси кипящей воды и сухого насыщенного пара. Эта двухфазная равновесная система называется насыщенным (влажным) паром. При дальнейшем изобарном подводе теплоты сухой насыщенный пар превращается в перегретый (а). Перегретый пар имеет температуру выше температуры кипения (насыщения) при данном давлении.

Точки на линии a"-b"-с" характеризуют состояние сухого насыщенного пара, а кривая определяет зависимость удельного объема сухого пара от давления = f(p) и называется верхней пограничной кривой. Пограничные кривые

пересекаются в точке (К), называемой критической.