
Министерство образования Республики Беларусь
Министерство образования и науки Российской Федерации
Межгосударственное образовательное учреждение высшего образования
«Белорусско-Российский университет»
Кафедра «Техническая эксплуатация автомобилей»
Отчёт
по лабораторным работам
по дисциплине «Использование вычислительной техники на АТ»
Выполнил: ст. гр. АВТ-172
Ясинский И.С.
Проверил: ст. преподаватель
Пономарёва О.А.
Могилёв, 2021
Содержание
Лабораторная работа №1 3
Лабораторная работа №2 7
Лабораторная работа №3 11
Лабораторная работа №4 16
Лабораторная работа №5 22
Лабораторная работа №6 27
Лабораторная работа №7 32
Лабораторная работа №1
Определения уравнения регрессии на основе использования EXCEL
Цель работы: Приобретение навыков определения уравнения регрессии на основе использования EXCEL.
Задание для лабораторной работы:
1. Используя метод наименьших квадратов (МНК), построить уравнения регрессии для заданного варианта. (Линейную и нелинейную (квадратичную, кубическую) зависимости).
2. Построить графики экспериментальных и полученных теоретических данных.
3. Сравнить результаты.
Вариант 8
Таблица 1.1 – Исходные данные
Угол подъема, град. |
0 |
2 |
3 |
4 |
5 |
7 |
8 |
9 |
10 |
11 |
12 |
Сила сопротивления, кН |
100 |
107 |
110 |
113 |
117 |
124 |
127 |
131 |
134 |
137 |
140 |
Сила сопротивления перемещению транспортной машины в зависимости от угла подъема дороги приведены в таблице 1.1.
Выполнение
Переносим исходные данные из таблицы 1.1 в Excel (рисунок 1.1).
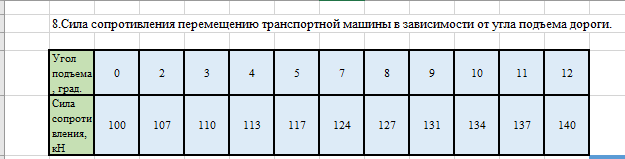
Рисунок 1.1 – Табличные данные в Excel
2. Для выполнения лабораторной работы нам понадобится поиск решения, чтобы добавить его во вкладку «Данные», нам необходимо выбрать его в «Надстройках», для этого переходим в Файл –Параметры– Надстройки (Из списка выбираем «Поиск решения») – Перейти - Ставим галочку напротив «Поиск решения» – Нажимаем «ОК»
3. Переходим во вкладку Данные и наблюдаем появление кнопки «Поиск решения»
4. Строим начальную диаграмму (рисунок 1.2) с заданными данными из таблицы 1.1.
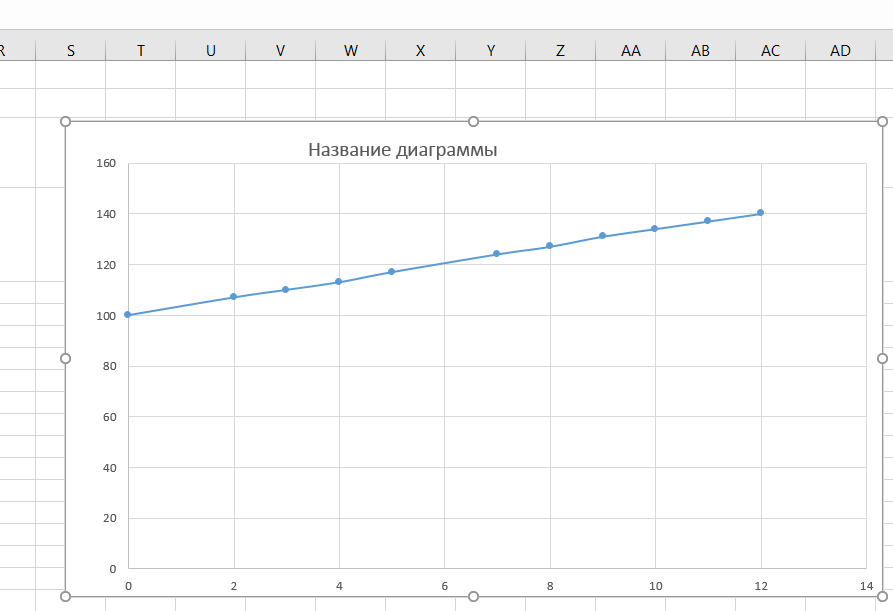
Рисунок 1.2 – Диаграмма рассеяния
5. Проведём регрессионный анализ с помощью средства «Поиск решения» на построения линейного, гиперболического, экспоненциального, степенного, параболического уравнения регрессии.
6. Рассчитываем коэффициенты линейной регрессии по формуле (1.1) и получаем промежуточные результаты, представленные на рисунке 1.3.
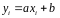 (1.1)
(1.1)
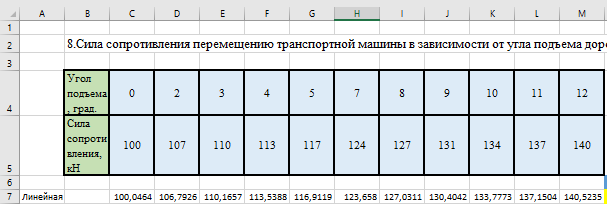
Рисунок 1.3 – Промежуточные результаты
Для решения этой задачи методом наименьших квадратов отведем под параметры a и b ячейки N6 и O7 соответственно. А в ячейку Q7 введем целевую функцию по формуле: = СУММКВРАЗН(C5:M5;C7:M7)
При этом предполагаем, а=0 и b=0.
Теперь выберем команду Данные-Поиск решения и заполним открывшееся диалоговое окно Поиск решения, как показано на рисунке 1.4.
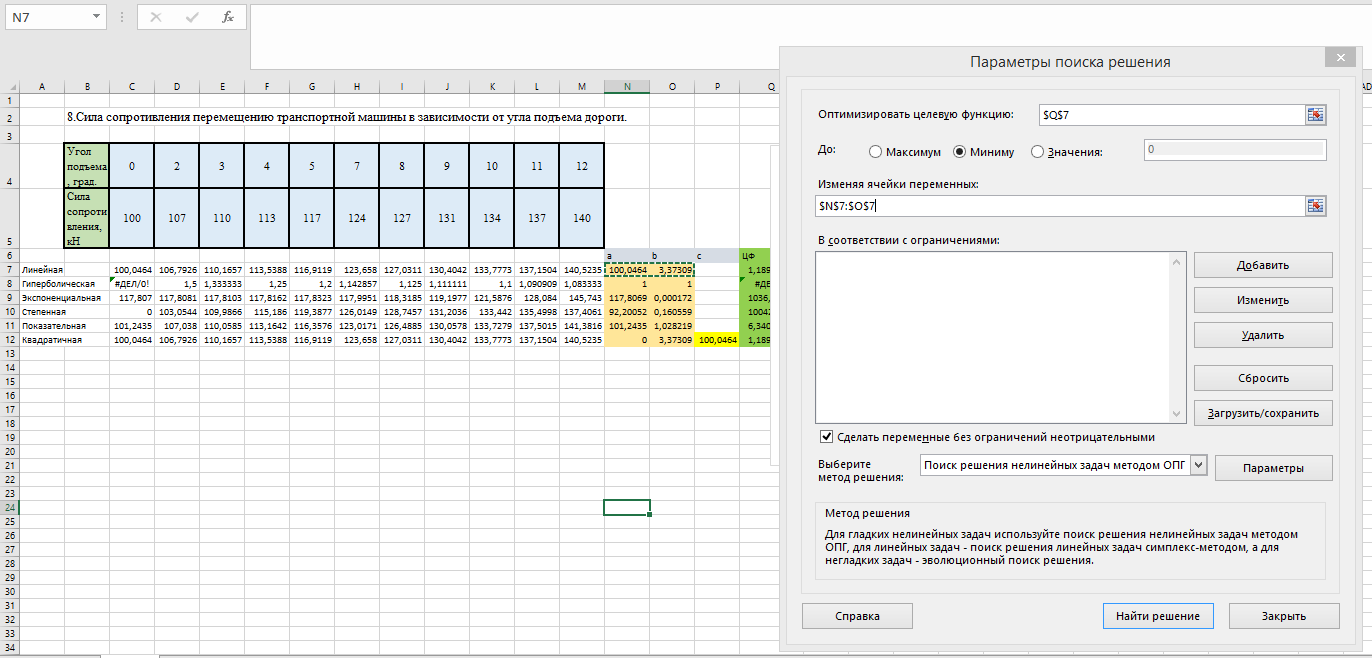
Рисунок 1.4 – Диалоговое окно Поиск решения
На рисунке 1.5 представлены графики диаграммы рассеяния и линейной регрессии.
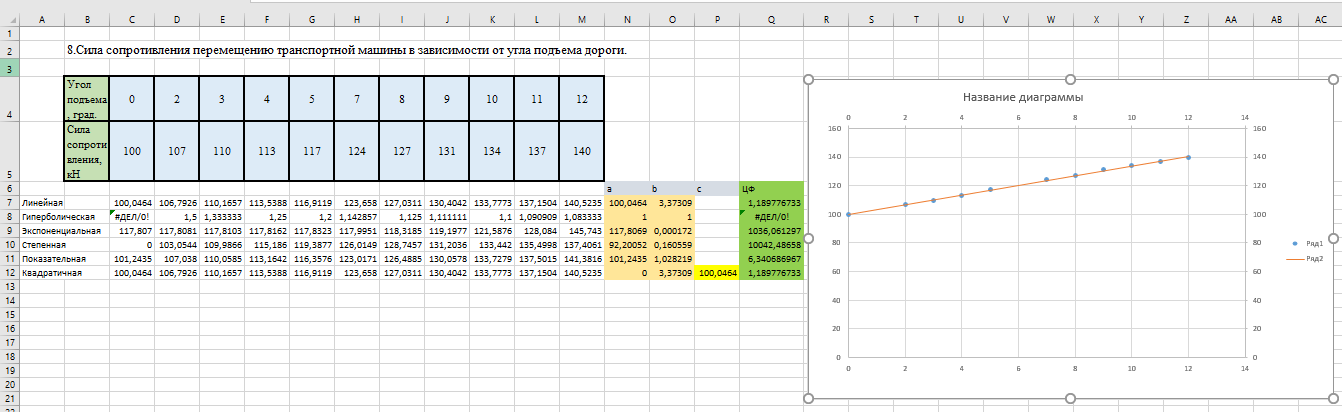
Рисунок 1.5 – Диаграмма рассеяния линейного уравнения
Далее аналогично по формулам найдем гиперболическое (1.2), экспоненциальное (1.3), степенное (1.4), параболическое (1.5), квадратичное (1.6) уравнение регрессии.
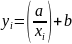 (1.2)
(1.2)
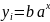 (1.3)
(1.3)
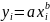 (1.4)
(1.4)
 (1.5)
(1.5)
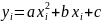 (1.6)
(1.6)
На рисунке 1.6 представлены результаты регрессионного анализа.
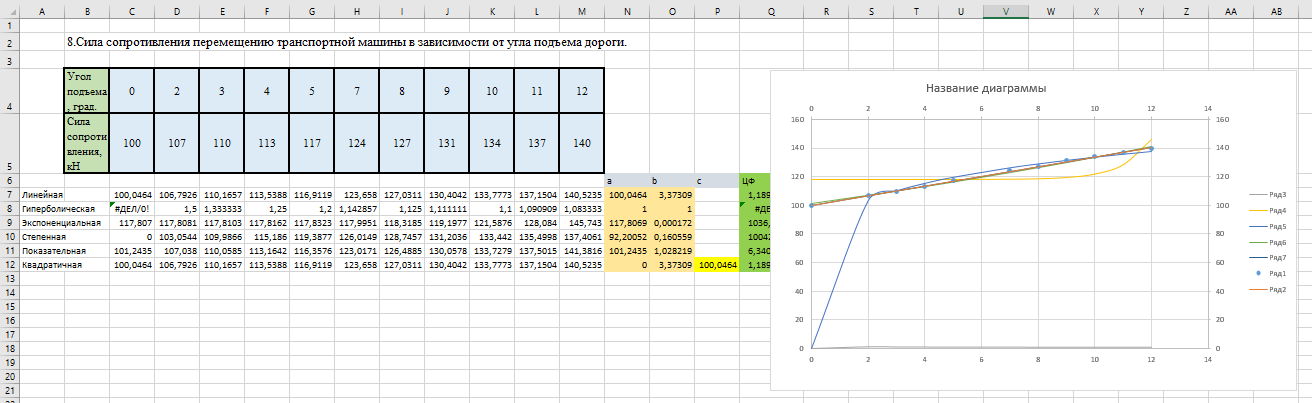
Рисунок 1.6 – Диаграмма рассеяния уравнений регрессии
Вывод
В ходе выполнения лабораторной работы используя метод наименьших квадратов, были построены уравнение регрессии экспериментальных и теоретических данных, из графика видно, что наиболее приближён к теоретическому график линейная, показательная и квадратичная функция.
