
Методические указания
.pdf
8.3. Передача непрерывных сигналов с дискретизацией во временном представлении.
Чаще всего информация, предназначенная для передачи или ввода в
ЦВМ, представляет собой непрерывно изменяющиеся физические величины, как, например, изменение температуры, давления, скорости, звука и т.п. Различного рода датчики, измеряющие эти величины, чаще всего выдают их в виде пропорционального изменения непрерывных электрических сигналов постоянного или переменного тока. Для обработки информации в ЦВМ или для передачи по дискретному каналу входные непрерывные величины необходимо представить в виде дискретных, по которым возможно восстановление первоначального сигнала, была обоснована В.А.Котельниковым.
Функции с непериодическим характером изменения могут быть представлены в виде бесконечно большого количества синусоидальных колебаний с соответствующими амплитудами и фазовыми сдвигами (интеграл Фурье). Иными словами, спектр непериодического сигнала в общем случае содержит все без исключения частоты от 0
до ∞ . Однако на практике используются функции с ограниченным спектром и временем. Функции же с ограниченным спектром и временем определяются вполне определенным конечным числом своих значений (ряд Фурье). Отсюда следует, что любая непрерывная функция с ограниченным спектром и временем может быть заменена вполне определенной последовательностью дискретных значений.
Отсюда также следует, что для построения непрерывной функции,
заданной спектром частот от 0 до ∞ необходимо знать все ее точки. Непрерывная функция с ограниченным спектром на конечном интервале времени может быть построена лишь по конечному числу дискретных значений, отстоящих друг от друга на вполне определенном расстоянии.
В.А.Котельников показал, то если функция f ()t не содержит частот выше Fщ, то она может быть определена совокупностью ординат,
отстоящих друг от друга на промежуток времени |
t = |
1 |
. Если |
|
2F |
||||
|
|
|
функция с указанным спектром частот рассматривается на некотором интервале времени T (рис.5.8а), то число дискретных ординат, определяющих функцию, будет:
L = Tt =2TF.
117

Доказательство теоремы Котельникова состоит в разложении функ-
ции f t в ряд особого вида. Для непрерывной непериодической |
||||||
() |
|
|
|
|
|
|
функции в общем случае имеем соотношение |
|
|||||
f t |
|
= |
1 |
+∞S(ω)e jωt dω, |
(8.1) |
|
|
2π |
|||||
() |
|
|
∫ |
|
||
где |
|
|
|
|
−∞ |
|
) |
|
∫ |
|
|
||
( |
|
|
|
|||
S ω |
|
|
=+∞ f (t)e− jωt dt |
(8.2) |
||
−∞
Для функции с ограниченным спектром вместо 8.1 запишем:
|
|
f t |
= |
|
1 |
|
+ωc |
S(ω)e jωt dω, |
|
(8.3) |
|||||||
|
|
2π |
|
∫ |
|
||||||||||||
|
|
() |
|
|
|
|
|
|
|
|
|
|
|
|
|||
( |
) |
=0 при |
|
|
|
−ωc |
|
|
|
c |
|
() |
|
( ) |
|||
−ω |
c |
>ω >ω |
и |
=0 |
|||||||||||||
при этом S ω |
|
|
|
f t |
. Функция S ω |
||||||||||||
на конечном интервале |
[ |
|
|
|
|
|
] |
может быть разложена в ряд Фу- |
|||||||||
|
−ω c,ω |
|
|||||||||||||||
рье по частотам следующим образом:
S(ω)= ∑∞ Ck e jkω t
k =−∞
или при рассмотрении значений:
t = π ; ωc = π =π f ; 2ωc =2π
ωc t
где 2ωc играет роль периода по частоте, получим:
( ) |
∞ |
|
jπ k |
ω |
|
|
|
|
|||
∑ k |
ωc |
|
|||
S ω = |
|
C e |
. |
||
|
|
|
|||
k =−∞
f ,
(8.4)
Коэффициенты ряда Фурье определяются по обычной формуле:
|
1 |
+ω∫c S(ω)e− jπ k |
ω |
|
|||
|
|
|
|
||||
C = |
ωc dω |
(8.5) |
|||||
|
|||||||
k |
2ωc −ω |
c |
|
|
|
||
|
|
|
|
|
|
||
Подставляя 8.4 в 8.3 получим:
118
|
|
1 |
+ω |
|
∞ |
jπ k |
ω |
|
|
|
|
|
|
|
|
||||||
() |
|
|
c |
|
ωc |
jωt |
|
|||
= |
|
∫ |
|
∑e |
|
|
|
|
dω |
|
f t |
2π |
|
|
|
|
e |
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
−ωc k =−∞ |
|
|
|
|
|
||
или, изменяя порядок действий:
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
1 |
∞ |
|
|
+ω |
c |
|
jω t+ k |
|
|
|
|
|
|
|
|
||||||
() |
|
|
k |
∫ |
|
|
|
|
|||
|
∑ |
|
|
|
|
ωc dω , (8.6) |
|||||
f t |
= |
|
|
C |
|
|
|
e |
|
||
|
|
2π k=−∞ |
|
−ωc |
|
|
|
|
|||
откуда после интегрирования находим:
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
sinωc t+ k |
|
|
|
||
() |
= |
∞ |
C |
|
|
|
ωc |
|
|||
|
|
∑ |
k |
|
|
|
|
(8.7) |
|||
f t |
|
|
|
|
|
π |
|
|
|||
|
|
π k=−∞ |
|
t + k |
|
|
|
||||
|
|
|
|
|
|
|
ωc |
|
|
|
|
Возьмем интеграл в равенстве 8.6
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
∞ |
|
|
|
+ω |
c |
|
|
|
jω t+ k |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωc |
|
|
|
|
|
|||||
f t |
= |
|
∑ |
C |
k |
∫ |
|
e |
|
|
|
dω = |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
() |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2π k=−∞ |
|
−ωc |
|
|
|
|
|
|
|
|
+ωc |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
jω t+ k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
e |
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
||||||
= |
|
|
|
∑Ck |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
2π k=−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
+ k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
j t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωc |
|
−ω |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
π |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
jω |
t+ k |
|
|
|
|
|
|
|
|
− jω t+ k |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
|
ω |
|
|
|||||||||||||
|
1 |
|
|
∞ |
|
|
e |
c |
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
c −e |
|
|
|
|
c |
|
|||||||||||||
= |
|
|
|
|
∑Ck |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
||||||||
|
|
2π k=−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j t + k |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωc |
|
|
|
|
|||||
119
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
π |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
cosωc t + k |
|
|
|
|
|
|
+ j sinωc t + k |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
ωc |
|
|
|
|
|
ωc |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
π |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= |
|
1 ∑Ck |
−cosωc t + k |
ωc |
|
|
+ j sinωc t + k |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ωc = |
|||||||||||||
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π k =−∞ |
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
j t + k |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωc |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= |
|
|
|
|
sinωc t + k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 ∑Ck |
|
|
ωc . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π k=−∞ |
t + k |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
ωc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сопоставим выражения 8.3 и 8.5. Приведем выражение под интегралом равенства 8.3 к выражению под интегралом равенства 8.5.
Учитывая, что |
|
t = |
|
π |
|
и k |
t =k |
|
π |
, запишем равенство 8.3 в |
|||||||||||
|
ωc |
|
|
|
|||||||||||||||||
виде: |
|
|
|
|
|
|
|
|
|
|
|
ωc |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|||
|
|
|
|
|
π |
|
|
|
|
|
1 |
+ωc |
|
|
|
− jπ k |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
|||||||
f |
−k |
|
|
|
|
|
= |
|
∫ |
|
S(ω)e |
|
c dω |
(8.3’) |
|||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
ωc |
|
|
2π |
−ωc |
|
|
|
|
|
|
|
|
|||||
из 8.3’ и 8.5: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2ω Ck =2π f |
−k |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
ωc |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|||
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ck |
= |
|
|
|
|
|
f |
−k |
|
. |
|
|
|
|
|
|
(8.8) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
ω c |
|
|
|
ωc |
|
|
|
|
|
|
|
||||||||
Подставим 8.8 в 8.7 и, изменяя знаки под знаком суммы (так как суммирование производится по всем к от – ∞ до + ∞), получим:
120
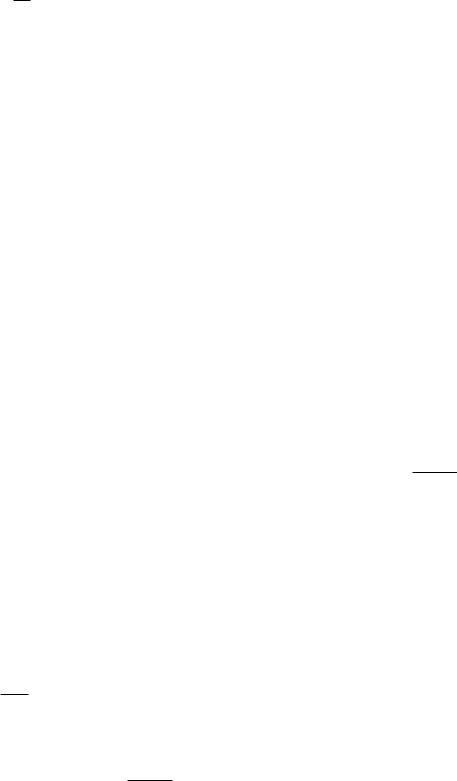
f (t)= 1 ∑∞
π k=−∞
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
π |
|
|
π |
|
sinωc t +k |
|
|
|
|
|
|
|
ωc |
|
|||||||
|
|
−k |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
||||
|
f |
|
|
|
|
|
|
|
||
ωc |
|
|
ωc |
|
|
|
|
|
(8.9) |
|
|
|
|
|
|
|
|||||
= ∑∞ |
f (k t) |
sinωc (t −k t) |
. |
|
|||
k=−∞ |
|
ωc (t −k t) |
|
Таким образом, функция с ограниченным спектром может быть представлена рядом 8.9, коэффициенты которого представляют собой отсчеты значений функции, взятые через интервалы времени:
t = |
π |
= |
1 |
. |
|
|
|
||||
ω |
c |
|
2F |
||
|
|
|
c |
||
В этом и состоит доказательство теоремы Котельникова. Особое свойство ряда 8.9 состоит в том, что значение суммы в моменты времени k t определяется только k -м слагаемым (рис.8.1б), так как все остальные слагаемые в этот же момент времени t равны нулю, т.е.
sin |
ω |
c (t |
− |
k t) |
1 |
при |
t =k |
t, |
||
|
|
|
|
= |
|
|
t (h≠k). |
|||
ω |
c |
(t −k |
t) |
0 |
при |
t=h |
||||
|
|
|
|
|
|
|
|
|
|
|
sinγ
γ
отметим, что функция равна 1 при γ =0 , а при возрастании эта
функция, колеблясь, убывает.
Рассмотрим смысл теоремы Котельникова графически. Пусть необходимо передать некоторую непрерывную функцию f ()t (рис.8.1а). Предположим, что спектр функции ограничен сверху частотой ωc . Производя отсчеты мгновенных значений функции в моменты вре-
мени t = π ; 2 t; 3 t; Kполучим картину, представленную на
ωc
рис.8.1б.
Каждая их функций вида sinγ γ представляет собой изменение во времени напряжения на выходе идеального фильтра, пропускающего
121
все частоты от 0 до граничной ωc при подаче на вход фильтра на-
пряжения в форме короткого импульса.
Таким образом, если сложить полученные составляющие суммы 8.9, то с ограничениями, о которых будет сказано ниже, вновь получим функцию f ()t .
Дело в том, что для точного воспроизведения функции в соответствии с разложением 8.9 необходимо знать значения ее ординат справа и слева от заданного интервала, так как они влияют на функцию, т.е. для точного воспроизведения функции необходимо рассмотреть функцию на бесконечном интервале. При рассмотрении функцией на ограниченном интервале и с ограниченным спектром теорема В.А.Котельникова дает приближенное решение. Характер ошибки в воспроизведении функции представлен на рис.5.8в.
Отметим дополнительно, что функция рассматривается в промежут-
ке времени T , то число ординат, которое потребуется, будет
L = Tt =2TFc,
где t = 21Fc – согласно теореме Котельникова, а Fc — макси-
мальная частота спектра передаваемого сигнала.
С другой стороны, при кодо-импульсной передаче (КИМ) время t
представляет собой период повторения, а 1t = FП частоту повто-
рения кодовых групп, вследствие чего FП ≥2Fc , т.е. частота по-
сылки амплитудных значений функции f ()t должна быть равна не
менее чем удвоенной частоте верхней границы спектра передаваемого сигнала.
Если частотный спектр функции занимает полосу частот от F1 до F2 , что в соответствии с теоремой В.А. Котельникова будут иметь
место соотношения:
t′= 2(F21−F1 ); L′=2(F2 −F1 )T.
Таким образом, теорема Котельникова указывает технический способ передачи функции f ()t с ограниченным спектром и восстановление ее на приемном конце. Этот способ сводится к следующему:
122

1.Берутся отсчеты f (k t)функции f ()t в моменты времени k t .
2.Полученные значения чисел передаются по системе связи любым способом (например, посредством двоичного кода).
3.В месте восстановления сигнала должны быть получены короткие импульсы соответствующей высоты.
4.Импульсы подаются на фильтр с верхней границей пропускания частот ωc , на выходе которого получим исходную функцию f ()t .
Вкачестве общего вывода можно отметить, что передача как непрерывных, так и дискретных сообщений (функций) сводится в конечном счете к передаче последовательности дискретных чисел.
8.4. Передача непрерывных сигналов с дискретизацией
вчастотном представлении.
Впредыдущем случае спектр функции был ограничен по частоте, т.е. f ()t =0 , если −ω c >ω >ωc . Теперь в качестве исходной
возьмем функцию, ограниченную во времени. При этом f ()t =0 , если T1 >t >T2 .
В общем случае для непериодической функции имеем:
f (t)= 21π +∫∞S(ω)e jωt dω,
−∞
S(ω)=+∫∞ f (t)e− jωt dt
(8.11)
(8.12)
−∞
Рассмотрим спектральное выражение функции f ()t для данного случая. Тогда равенство 8.12 можно записать
( ) |
∫ |
|
S ω |
=T2 f (t)e− jωt dt. |
(8.13) |
T1
Функцию f ()t можно разложить в ряд Фурье на интервале от T1 до
T2 :
123

|
|
|
|
|
|
() |
|
|
∑ k |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
f t |
= |
∞ C |
e jkω t |
|
|
||||||||
или, т.к. |
|
|
|
|
|
k=−∞ |
|
|
|
|
|
|
|
|
|||||
|
|
|
ω = 2π = |
|
2π |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
, |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
T |
|
T |
|
−T |
|
|
|
|
|||
то |
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2π k |
t |
|||||
|
|
|
|
|
|
|
|
|
∞ C |
e j |
|||||||||
|
|
|
|
|
|
f t |
= |
T2−T1 |
, |
||||||||||
|
|
|
|
|
|
() |
|
|
∑ k |
|
|
|
|
|
|
|
|
||
где |
|
|
|
|
|
|
|
k=−∞ |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
2π k t |
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
T∫2 |
f (t)e− j |
|
|
|
|
|
1 |
|
||||||
C |
= |
|
|
T2 |
−T1 dt |
= |
|
|
|
|
|||||||||
|
|
|
T |
|
−T |
||||||||||||||
k |
T |
−T |
1442443 |
|
|
||||||||||||||
|
2 |
|
1 T1 |
|
) |
|
|
|
|
2 |
|
1 |
|||||||
S 2π k ,T2 −T1
(8.14)
(8.15)
причем *) — это равенство 8.13 при
ω = 2π ; |
kω = |
2π k |
=ω |
; |
k — номер наивысшей гармо- |
|||
|
||||||||
T |
|
|
c |
|
|
|
|
|
|
T2 −T1 |
|
|
2π k |
|
|
||
ники определяется из соотношения |
|
=ω |
, так как практиче- |
|||||
|
|
|||||||
|
|
|
|
|
|
T |
c |
|
|
|
|
|
|
|
|
|
|
ски функция ограничена и по частоте.
Функция f ()t полностью определяется при ее разложении в ряд
Фурье на |
интервале |
T1 <t <T2 |
коэффициентами |
спектральной |
|||||||||||||||||||
|
|
( |
) |
в точках: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
функции S ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
ωc |
=k |
|
|
|
=kω; |
|
(8.16) |
||||||||
|
|
|
|
|
|
|
|
T |
−T |
|
|||||||||||||
|
|
2π |
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
||||
где ω = |
|
|
|
, k |
– принимает все отрицательные и положи- |
||||||||||||||||||
|
−T |
||||||||||||||||||||||
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
тельные значения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Подставим 8.15 в 8.14, тогда |
|
|
|
|
|
|
|
|
|
|
2π k t |
|
|
||||||||||
|
|
|
|
|
|
|
∞ |
|
|
1 |
|
|
|
|
|
2π k |
|
j |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
T2 −T1 |
|
|
||||||||
|
|
f |
t |
= |
|
|
|
|
|
S |
|
|
|
|
. |
(8.17) |
|||||||
|
|
k=−∞∑ T |
−T |
|
T −T |
e |
|
|
|||||||||||||||
|
|
|
() |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
2 |
1 |
|
|
|
|
|
|||
124

( |
) |
представляет |
|
собой |
спектр функции |
||
Таким образом, если S ω |
|
|
|||||
() |
|
1 |
2 |
( |
) |
однозначно |
|
f t равной нулю вне интервала T <t <T |
, то |
S ω |
|
||||
определяется последовательностью ее значений в точках, отстоящих
1
друг от друга на расстоянии T2 −T1 (Гц).
Так как
S ω |
= |
+∞ f (t)e− jωt dt = |
+∞ f (t)cosω tdt − j |
+∞f (t)sinω tdt, |
( ) |
|
∫ |
∫ |
∫ |
|
|
−∞ |
−∞ |
−∞ |
|
|
|
то S(kω) как комплексное число может быть определено двумя значениями: вещественной и мнимой частью, а следовательно, для определения самой функции f ()t на интервале T2 −T1 потребуется L =2k =2FcT чисел.
Так как ω |
c |
= 2πk |
, то k = |
T 2π Fc |
=T F . |
||||
|
|||||||||
|
T |
|
|
2π |
|
|
c |
||
|
|
|
|
T |
|
||||
Во временном изображении — |
L = |
=2F T . |
|||||||
|
|||||||||
|
|
|
|
|
|
t |
c |
||
|
|
|
|
|
|
|
|||
Таким образом, функция с ограниченным спектром Fc и конечной длительностью T определяется L =2FcT числами независимо от
того, будут ли этими числами мгновенные значения функции, отсчитанные через t или спектральные коэффициенты разложения в ряд Фурье 8.16. По аналогии с дискретным представлением непрерывной функции во временном изображении выведем аналитическое
выражение для спектральной функции S(ω) , заданной ее значениями в точках отсчета.
Выражение спектральной плотности S(ω)для функции f ()t ограниченной на интервале от T1 до T2 имеет вид 8.13. Сама же функ-
ция может быть представлена в виде разложения в ряд Фурье в комплексной форме 8.14.
Обозначим
T =T |
; |
T =−T . |
(8.18) |
||
2 |
2 |
|
1 |
2 |
|
|
|
|
|
||
Подставим 8.14 и 8.18 в 8.13 :
125
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π kt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
2πk |
|
||||||||||
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
j |
|
|
|
− jωt |
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
− jt ω− |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|||||||||||||||||||||||||||||||||
S |
ω |
= |
2 |
|
|
|
|
|
e |
|
|
|
T |
|
|
|
|
|
|
dt = |
|
|
|
C |
|
2 |
e |
|
|
dt = |
||||||||||||||||||||||||||||||||||||
∫ |
|
|
∑C |
k |
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
∑ |
k ∫ |
|
|
|
||||||||||||||||||||||||||||||||||||
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
T k |
=−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k=−∞ |
|
|
T |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2πk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
− jt ω− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
∞ |
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
∑Ck |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2πk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
k=−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
− j ω − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Tω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
− jt |
|
|
|
|
|
−πk |
|
|
|
|
|
jt |
|
|
|
|
|
|
−πk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
∞ |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
−e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
= |
∑Ck |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
k=−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2πk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
− j ω |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
Tω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
|
−π k − j sin |
|
|
|
|
|
|
|
|
|
−π k |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Tω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tω |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
−cos |
|
|
|
|
|
|
|
|
|
|
−π k |
− j sin |
|
|
|
|
|
|
|
−π k |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
∞ |
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
= |
∑Ck |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2πk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
k=−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− j ω − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
1 |
|
|
|
2π k |
|
−2 j sin |
|
|
|
|
|
|
|
−π k |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
∞ |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
= |
∑ |
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
k=−∞T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− j |
|
|
|
|
|
|
|
|
|
|
|
|
|
−π k |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Окончательно имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π k |
sin |
|
|
|
|
|
|
|
|
|
−π k |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
( |
|
) |
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
S ω |
|
= |
|
|
|
|
|
|
S |
|
T |
|
|
|
|
|
Tω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(8.19) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
k=−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
−π k |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
126
