
- •Определение параметров модели продольного движения судна
- •Введение.
- •Задание
- •Часть 1. Геометрические характеристики
- •Часть 2. Водоизмещение и Коэффициенты полноты
- •Часть 3. Определение сопротивления движению судна на тихой воде
- •Часть 4. Определение аэродинамического сопротивления
- •Часть 5. Определение сопротивления руля
- •Часть 6. Определение дополнительного сопротивления на волнении
- •Часть 7. Определение присоединенных масс корпуса
- •Часть 8. Определение параметров гребного винта и сил от него
- •Список терминов, обозначений, сокращений
- •Способы приближенного определения остаточного сопротивления судна на основании серийных испытаний моделей
- •Серия судов полных обводов.
- •Пример выполнения задания
- •Список литературы
Серия судов полных обводов.
Крупнотоннажные танкеры и рудовозы с коэффициентами общей полноты 0,80 начали применяться сравнительно недавно. Поэтому известно относительно небольшое количество экспериментальных исследований сопротивления этих объектов. Помимо систематической серии моделей, испытанной исследовательским институтом судостроения в Токио (см. табл. П.1, п.5) [101], наиболее крупным исследованием в этой области является отечественная серия судов с большой полнотой обводов (см. табл. П.1, п.4) [4б]. Основные геометрические характеристики судов этой серии приведены в табл. П.1.
Теоретические чертежи корпуса моделей для исследованных вариантов обводов носовой и кормовой оконечностей приведены на рис. П.18 и П.19 соответственно. На рис. П.20 изображены контуры штевней тех же моделей.
Как видно из перечня варьируемых параметров (табл. П.1), в серии большое внимание уделялось исследованию различных форм носовой и кормовой оконечностей. По гидродинамическим особенностям воздействия на обтекание корпуса и его сопротивление, рассматриваемым в гл. ПI, все исследованные носовые обводы можно подразделить на обводы с заострением ГВЛ (бульбовые) и обводы с притуплением носовой ветви ГВЛ (цилиндрические, таранно-конические).
При расчете сопротивления судна в соответствии с традиционной схемой разделения на составляющие коэффициент для всех рассматриваемых форм обводов определяется по формуле
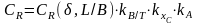 (П.8)
(П.8)
где
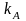 — коэффициент,
учитывающий различия в форме кормовых
обводов по сравнению с U-образной,
принятой в качестве основной.
— коэффициент,
учитывающий различия в форме кормовых
обводов по сравнению с U-образной,
принятой в качестве основной.
Коэффициент
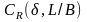 снимается с диаграмм рис. П.21—П.23 для
соответствующей формы носовой
оконечности с линейной интерполяцией
по коэффициенту
.
Коэффициент
,
учитывающий несоответствие расчетного
и стандартного значений В/Т,
для всех вариантов носовых обводов
определяется по графику на рис. П.24.
Коэффициент
снимается с диаграмм рис. П.21—П.23 для
соответствующей формы носовой
оконечности с линейной интерполяцией
по коэффициенту
.
Коэффициент
,
учитывающий несоответствие расчетного
и стандартного значений В/Т,
для всех вариантов носовых обводов
определяется по графику на рис. П.24.
Коэффициент
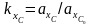 вычисляется
как отношение значений коэффициента
влияния
вычисляется
как отношение значений коэффициента
влияния
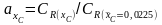 определяемых для расчетного значения
стандартного значения
определяемых для расчетного значения
стандартного значения
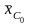 ,
указанного для различных
на рис. П.21—П.23. Коэффициенты влияния
,
указанного для различных
на рис. П.21—П.23. Коэффициенты влияния
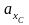 для носовых обводов с заострением и
притуплением ГВЛ снимаются с диаграммы
рис. П.25. В случае, если кормовые обводы
отличаются от U-обраэных, вводится
поправочный коэффициент
для носовых обводов с заострением и
притуплением ГВЛ снимаются с диаграммы
рис. П.25. В случае, если кормовые обводы
отличаются от U-обраэных, вводится
поправочный коэффициент
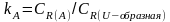 ,
значения которого находятся по табл.
П.3.
,
значения которого находятся по табл.
П.3.
Приближенное определение сопротивления по схеме, основанной на разделении его на физические составляющие с использованием материалов серии производится по следующей формуле:
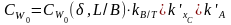 (П.9)
(П.9)
Коэффициент
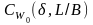 определяется как разность значений
коэффициентов
для расчетного числа Fr
и минимального значения Fг
== 0,10;
определяется как разность значений
коэффициентов
для расчетного числа Fr
и минимального значения Fг
== 0,10;
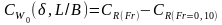 ,
снимаемых с диаграмм рис. П.21—П.23 с
линейной интерполяцией по
.
Коэффициент
определяется для всех вариантов носовых
обводов по графику рис. П.24. Аналогично
расчету по формуле (П.8), коэффициент
находится как отношение
,
снимаемых с диаграмм рис. П.21—П.23 с
линейной интерполяцией по
.
Коэффициент
определяется для всех вариантов носовых
обводов по графику рис. П.24. Аналогично
расчету по формуле (П.8), коэффициент
находится как отношение
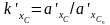 .
Коэффициенты
.
Коэффициенты
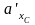 и
и
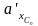 снимаются для расчетного и стандартного
значений
и
диаграмм на рис. П.26, построенных для
носовых обводов с заострением и
притуплением ГВЛ соответственно.
Коэффициент влияния формы кормы
снимаются для расчетного и стандартного
значений
и
диаграмм на рис. П.26, построенных для
носовых обводов с заострением и
притуплением ГВЛ соответственно.
Коэффициент влияния формы кормы
 определяется по табл. П.5.
определяется по табл. П.5.
Коэффициент влияния формы на вязкостное сопротивление рассчитывается по формуле
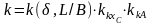 (П.10)
(П.10)
Коэффициент
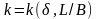 определяется по диаграммам на рис. П.27
для соответствующей формы носовой
оконечности. Коэффициент
определяется по диаграммам на рис. П.27
для соответствующей формы носовой
оконечности. Коэффициент
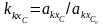 рассчитывается так же, как аналогичные
коэффициенты в формулах (П.8) и (П.9), причем
коэффициенты
рассчитывается так же, как аналогичные
коэффициенты в формулах (П.8) и (П.9), причем
коэффициенты
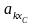 и
и
 снимаются с графика на рис. П.28 в
зависимости от характера носовых
обводов. Коэффициент
снимаются с графика на рис. П.28 в
зависимости от характера носовых
обводов. Коэффициент
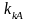 ,
применяемый в тех случаях, когда кормовые
обводы отличаются от U-образных,
,
применяемый в тех случаях, когда кормовые
обводы отличаются от U-образных,
 находится по графику на рис. П.29 для
соответствующей формы кормовой
оконечности.
находится по графику на рис. П.29 для
соответствующей формы кормовой
оконечности.
В
табл. П.6 приведен пример расчета по
материалам серии судов полных обводов
буксировочной мощности крупнотоннажного
судна для перевозки нефти и навалочных
грузов со следующими элементами: L
= 244,4 м; L/В
= 6,3; В/Т
= 2,67;
= 0,80;
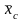 = 0,0358;
= 13960 м2;
цилиндрическими носовыми и V-образными
кормовыми обводами.
= 0,0358;
= 13960 м2;
цилиндрическими носовыми и V-образными
кормовыми обводами.
Серия 60. Одно из крупных зарубежных систематических исследований сопротивления и взаимодействия гребного винта с корпусом морских транспортных судов было проведено опытовым бассейном им. Д. Тейлора и известно под названием «Серия 60» [97]. Исходные модели серии отличаются пятью значениями коэффициента общей полноты (рр = 0,60; 0,65; 0,70; 0,75 и 0,80). Форма обводов исходных моделей характеризуется U-образными носовыми шпангоутами, значительным заострением носовых ветвей ватерлиний, кормовыми обводами крейсерского типа [12]. Результаты испытаний моделей серии пригодны для расчета сопротивления универсальных сухогрузных судов и среднетоннажных танкеров без носового бульба.
Помимо
коэффициента рр
в серии варьируются:
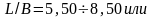
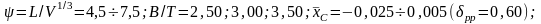
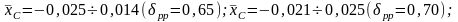
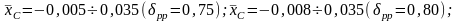
Общее
число испытанных моделей — 62. Характерный
теоретический чертеж одной модели
представлен на рис. П.30. Сведения об
условиях испытаний моделей приведены
в табл. П.1, п.1. В оригинальной обработке
результаты испытаний представлены в
виде диаграмм постоянных значений
удельного остаточного сопротивления
в функции от
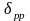 и
и
 ,
относительной скорости
и отношения В/Т.
При этом использовались английская
система мер, а в качестве экстраполятора
трения — формула Шенхерра (II.3).
,
относительной скорости
и отношения В/Т.
При этом использовались английская
система мер, а в качестве экстраполятора
трения — формула Шенхерра (II.3).

Рис. П.18. Теоретические корпуса носовой оконечности моделей серии крупнотоннажных танкеров и рудовозов: а - цилиндрическая оконечность; б – бульбообразная оконечность с заострением ГВЛ; в – таранно-коническая оконечность.
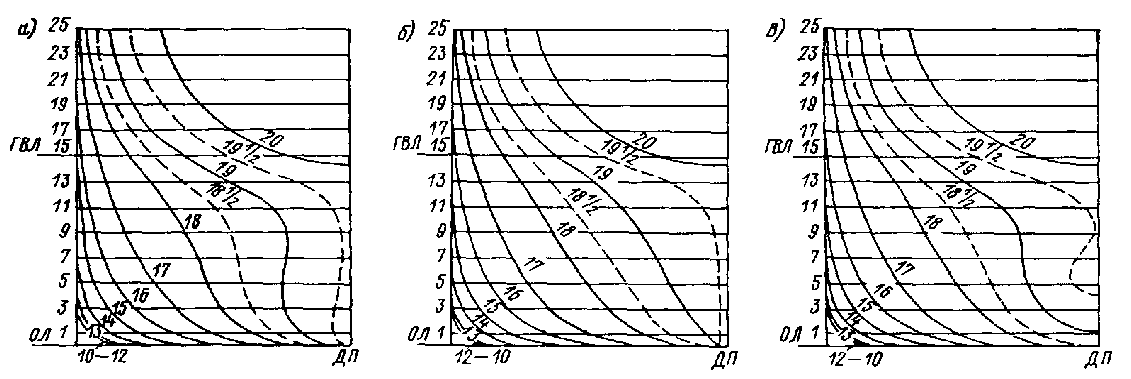
Рис. П.19. Теоретические корпуса кормовой оконечности моделей серии крупнотоннажных танкеров и рудовозов: а – U-образная оконечность; б – V-образная оконечность; в – сигарообразная оконечность.
С. П. Мурагиным материалы 60-й серии были переработаны с целью представления результатов в форме, принятой в отечественной практике. При этом сопротивление трения моделей определялось по формуле (II.4). Поэтому каких-либо поправок при использовании приведенных ниже диаграмм вводить не требуется.
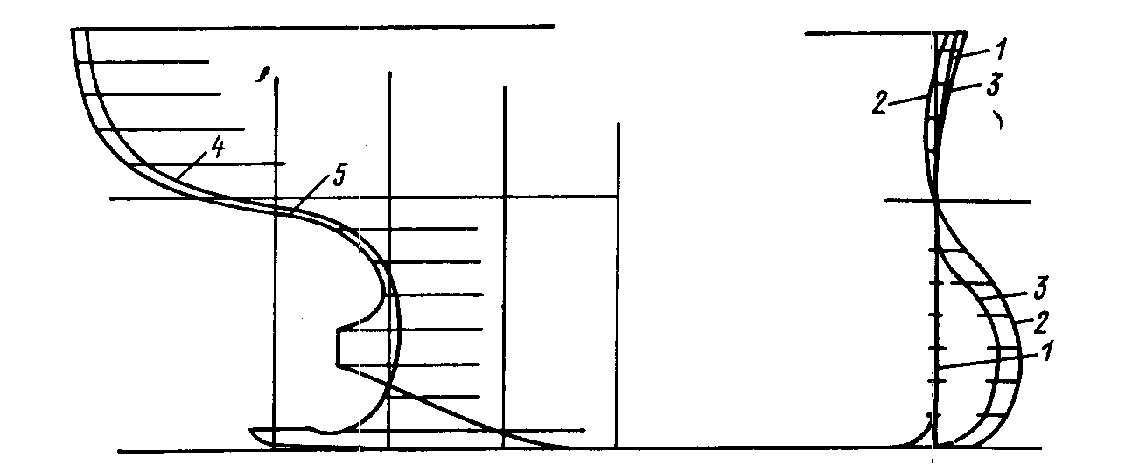
Рис. П.20. Очертания штевней моделей серии крупнотоннажных танкеров и рудовозов.
1. 2, 3 — цилиндрическая, бульбовая и таранно-коническая носовая оконечность соответственно; 4 — U- и V-образные кормовые оконечности; 5 — сигарообразная кормовая оконечность.
При расчете по диаграммам С. П. Мурагина коэффициент остаточного сопротивления определяется по формуле
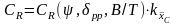 (П.11)
(П.11)
Таблица П.3. Поправочные коэффициенты на влияние формы кормовых обводов
Fr |
= 0,800 |
= 0,825 |
= 0,850 |
|||
V-образная |
Сигарообразная |
V-образная |
Сигарообразная |
V-образная |
Сигарообразная |
|
0,12 |
0,914 |
1,096 |
0,696 |
0,752 |
0,784 |
0,602 |
0,13 |
0,809 |
1,020 |
0,689 |
0,769 |
0,811 |
0,610 |
0,14 |
0,758 |
0,969 |
0.696 |
0,787 |
0,834 |
0,624 |
0,15 |
0,750 |
0,969 |
0,724 |
0,794 |
0,875 |
0,700 |
0,16 |
0,758 |
1,060 |
0,740 |
0,802 |
0,890 |
0,746 |
0,17 |
0,838 |
0,956 |
0,795 |
0,769 |
0,920 |
0,780 |
0,18 |
0,900 |
0,908 |
0,831 |
0,880 |
0,941 |
0,839 |
0,19 |
0,900 |
0,945 |
0,875 |
0,884 |
0,998 |
0,860 |
0,20 |
0,868 |
0,972 |
0,867 |
0,867 |
0,941 |
0,825 |
0,21 |
0,938 |
0,938 |
0,831 |
0,884 |
0,916 |
0,825 |
0,22 |
0,922 |
1,030 |
0,880 |
0,955 |
0,926 |
0,855 |
0,23 |
0,914 |
1,070 |
0,702 |
0,740 |
0,795 |
0,610 |
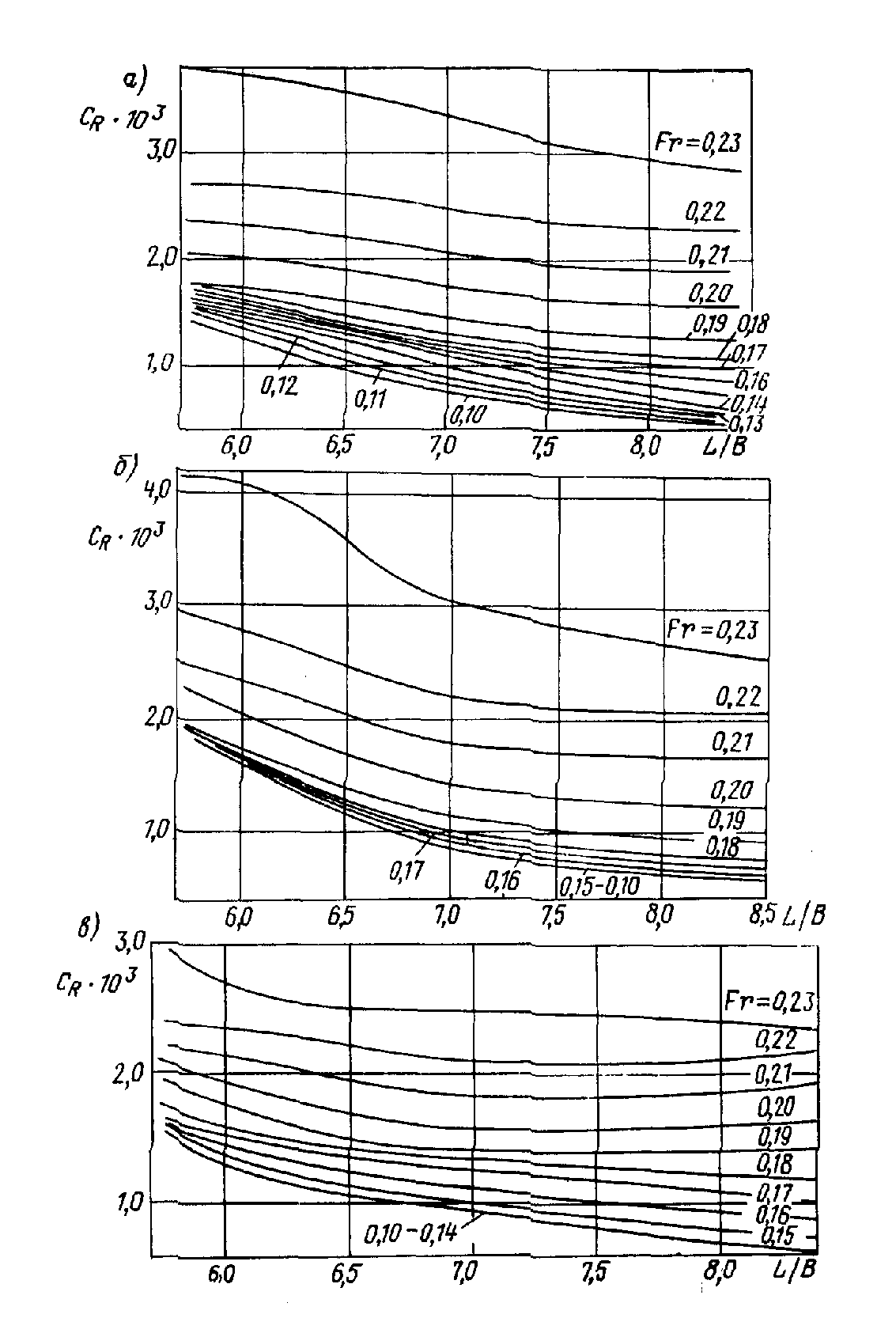
Рис. П.21. Зависимость от L/B ( = 0,800; В/Т = 2,7; =0,020);
а - цилиндрическая носовая оконечность; - бульбообразная носовая оконечность; в — таранно-коническая носовая оконечность.
Для определения
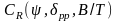 используется комплект диаграмм, на
каждой из которых приведена зависимость
коэффициента
от относительной длины
используется комплект диаграмм, на
каждой из которых приведена зависимость
коэффициента
от относительной длины
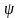 или отношения
L/В
(в качестве L
принята длина по грузовой ватерлинии)
при фиксированном значении
.
Группа из пяти диаграмм относится к
постоянному отношению BIT,
а именно: В/Т
= 2,50 — рис. П.31; BIT
= 3,0 — рис.
П,32; B/T
= 3,5 — диаграммы
рис. П.33. При этом применяется линейная
интерполяция по
и B/T.
или отношения
L/В
(в качестве L
принята длина по грузовой ватерлинии)
при фиксированном значении
.
Группа из пяти диаграмм относится к
постоянному отношению BIT,
а именно: В/Т
= 2,50 — рис. П.31; BIT
= 3,0 — рис.
П,32; B/T
= 3,5 — диаграммы
рис. П.33. При этом применяется линейная
интерполяция по
и B/T.
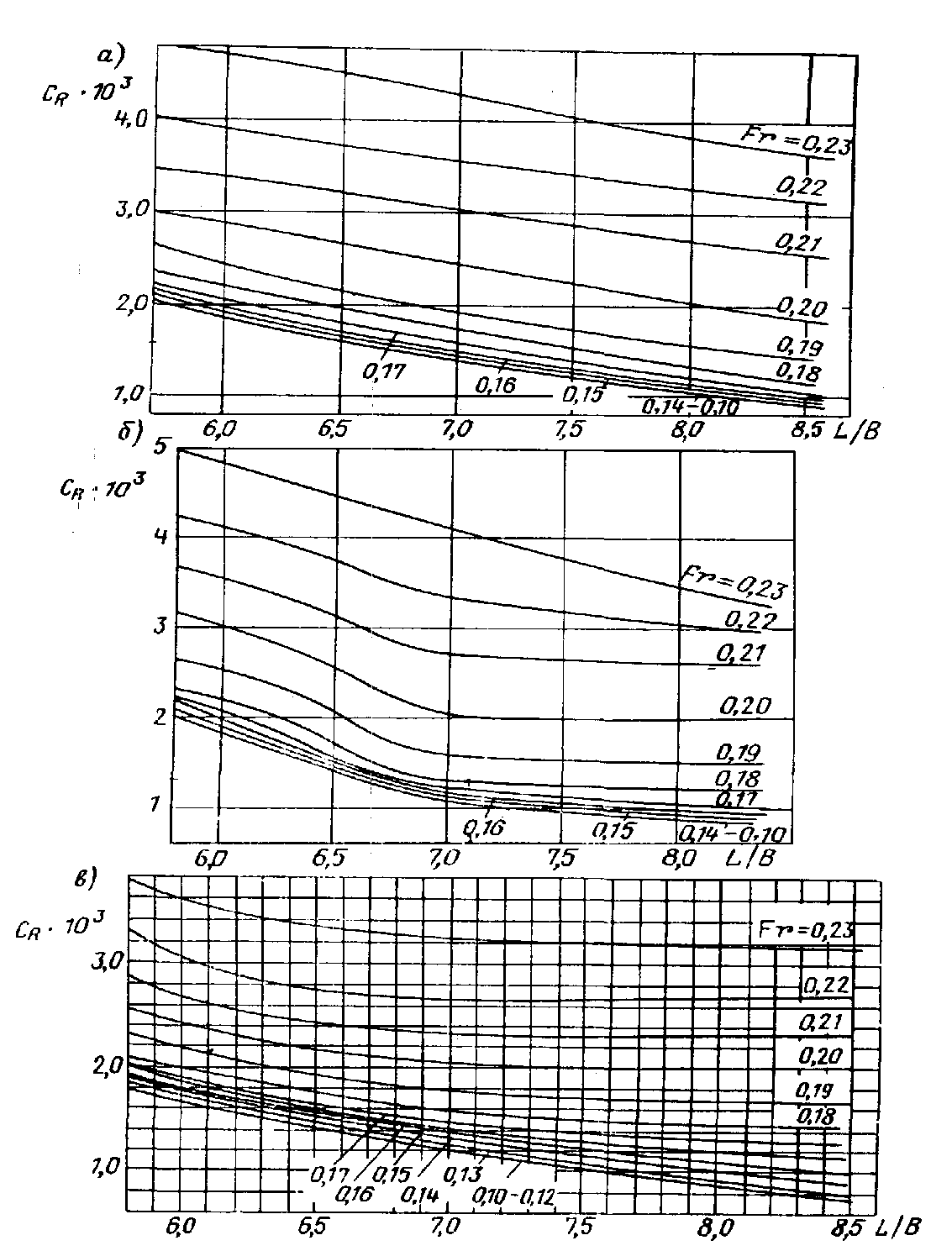
Рис. П.22. Зависимость
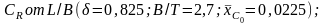 а – цилиндрическая носовая оконечность;
б – бульбообразная носовая оконечность;
в – таранно-коническая носовая
оконечность.
а – цилиндрическая носовая оконечность;
б – бульбообразная носовая оконечность;
в – таранно-коническая носовая
оконечность.

Рис. П.23. Зависимость
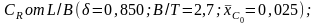 а – цилиндрическая носовая оконечность;
б – бульбообразная носовая оконечность;
в – таранно-коническая носовая
оконечность.
а – цилиндрическая носовая оконечность;
б – бульбообразная носовая оконечность;
в – таранно-коническая носовая
оконечность.
Таблица
П.4. Поправочные коэффициенты
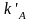 на влияние формы кормовых обводов
на влияние формы кормовых обводов
-
= 0,800
= 0,825
= 0,850
Fr
V-образная
Сигаро-
образная
V-образная
Сигаро-
образная
V-образная
Сигаро-
Образная
0,14
0,450
0,580
0,990
1,62
1,00
0,670
0,15
0,450
0,450
1,02
1,50
1,20
0,80
0,16
0,450
0,543
1,00
1,55
1,24
1,03
0,17
0,500
0,600
1,06
1,33
1,14
1,10
0,18
0,607
0,576
1,28
0,965
.1,15
1,08
0,19
0,892
0,600
1,17
0,964
1,13
1,12
0,20
0,883
0,766
1,11
1,06
1,18
1,08
0,21
0,825
0,870
1,01
0,970
1,02
0,940
0,22
0,962
0,837
0,915
0,970
0,970
0,910
0,23
0,925
1,002
0,970
1,05
0,975
0,942
Коэффициент
вычисляется как отношение коэффициентов
,
определяемых для расчетного значения
и базового
указанного на каждой диаграмме рис.
П.31—П.33 (в качестве базовых приняты
оптимальные значения
для каждого
).
Коэффициент
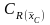 снимают с графиков рис. П.34, выбирая
диаграмму, соответствующую значению
,
наиболее близкому к расчетному.
снимают с графиков рис. П.34, выбирая
диаграмму, соответствующую значению
,
наиболее близкому к расчетному.
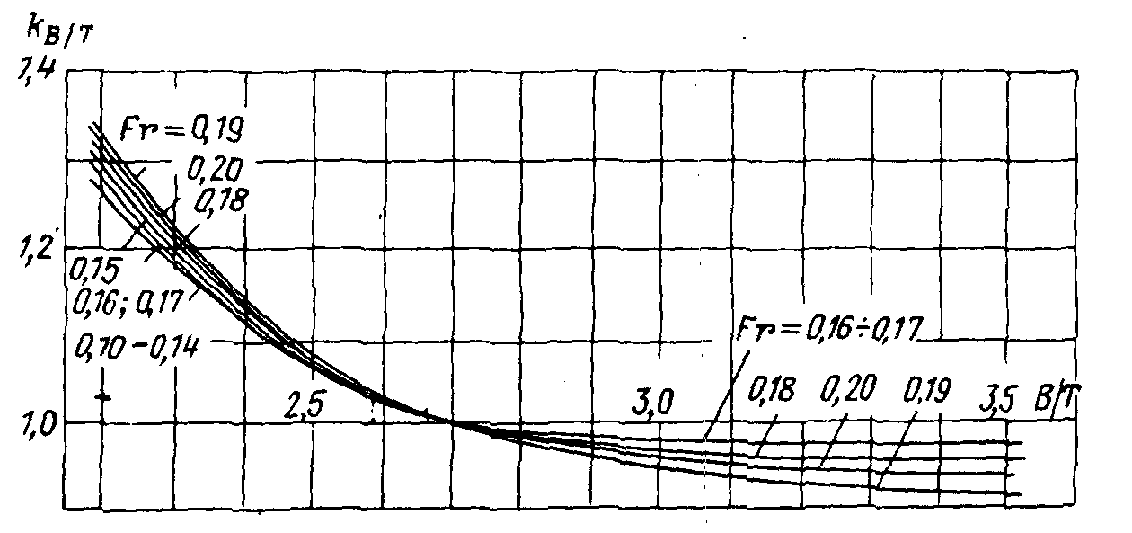
Рис. П.24. Зависимость
коэффициента влияния
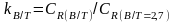
от В/Т.
Сэбит произвел обработку результатов испытаний моделей 60-й серии, также как и серии BSRA (табл. П.1, п. 7), в форме уравнений регрессии, позволяющих вычислять коэффициент полного сопротивления судна стандартной длины 400 фут [50]. Эти материалы с корректировкой на фактическую длину судна могут быть использованы при расчете сопротивления с применением ЭВМ.
Таблица П.5. Расчёт буксировочной мощности по материалам серии судов полных обводов.
№ п.п |
Обозначение расчётных величин |
Численные значения |
|||||
1 |
|
13 |
14 |
15 |
16 |
17 |
18 |
2 |
|
6,70 |
7,20 |
7,72 |
8,24 |
8,75 |
9,27 |
3 |
|
44,89 |
51,84 |
59,60 |
67,90 |
76,56 |
85,93 |
4 |
|
0,136 |
0,147 |
0,157 |
0,168 |
0,178 |
0,189 |
5 |
|
1,38 |
1,42 |
1,45 |
1,48 |
1,54 |
1,65 |
6 |
(см. Рис. П.24) |
1,0 |
1,0 |
1,0 |
1,0 |
1,0 |
1,0 |
7 |
|
0,650 |
0,660 |
0,679 |
0,705 |
0,760 |
0,875 |
8 |
(см. Табл. П.4) |
0,780 |
0,753 |
0,758 |
0,805 |
0,893 |
0,900 |
9 |
|
0,700 |
0,710 |
0,746 |
0,840 |
1,045 |
1,300 |
10 |
|
1,018 |
1,094 |
1,171 |
1,250 |
1,330 |
1,410 |
11 |
[по формуле (II.4)] |
1,567 |
1,553 |
1,540 |
1,528 |
1,516 |
1,505 |
12 |
|
0,10 |
0,10 |
0,10 |
0,10 |
0,10 |
0,10 |
13 |
|
0,05 |
0,05 |
0,05 |
0,05 |
0,05 |
0,05 |
14 |
|
2,420 |
2,413 |
2,436 |
2,518 |
2,711 |
2,950 |
15 |
, кН |
778,0 |
895,9 |
1039,8 |
1224,5 |
1486,5 |
1815,6 |
16 |
, кВт |
5210 |
6450 |
8030 |
10090 |
13010 |
16830 |
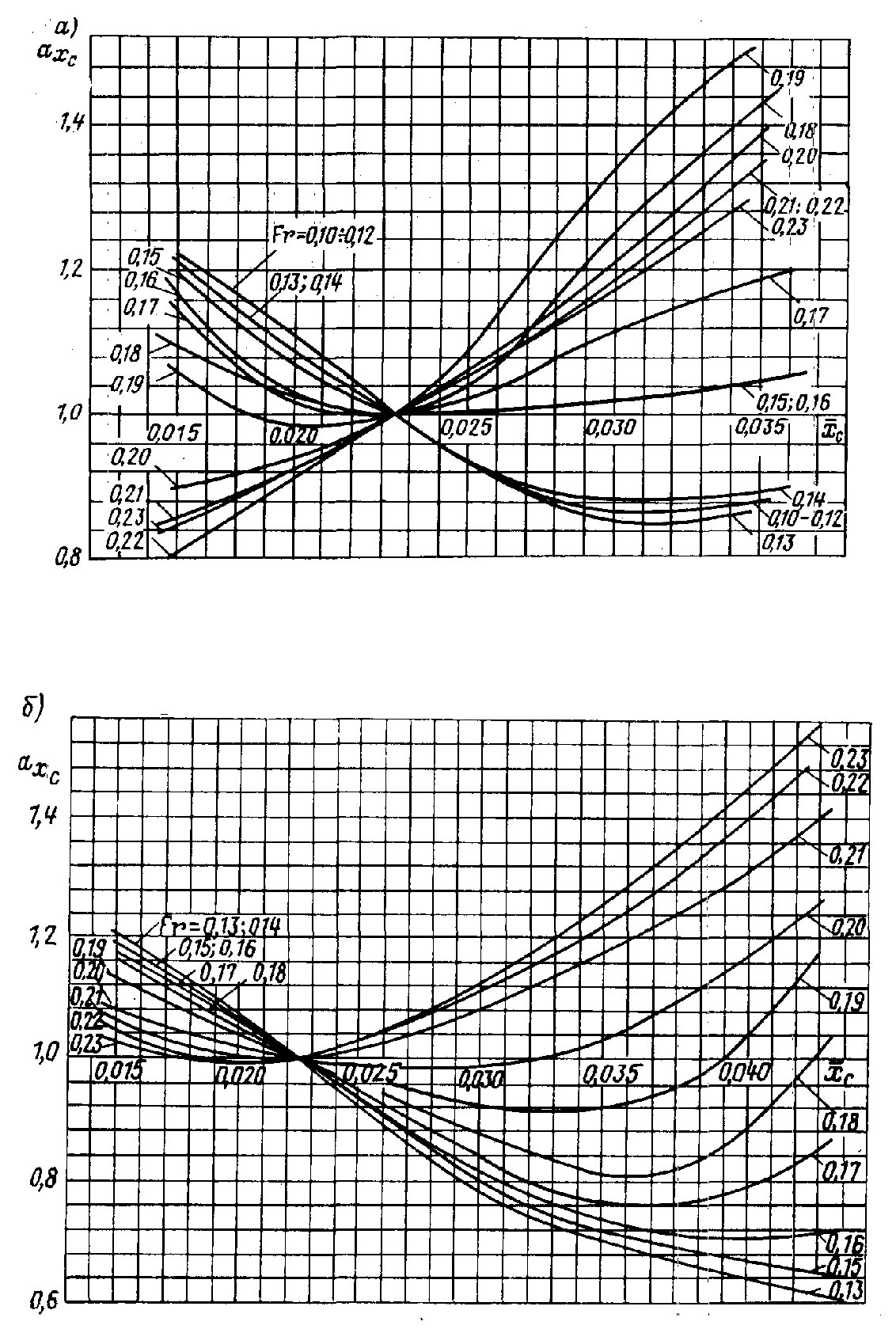
Рис.П.25. Зависимость коэффициента влияния от для носовых обводов: a – с заострением ГВЛ ; b – с притуплением ГВЛ .
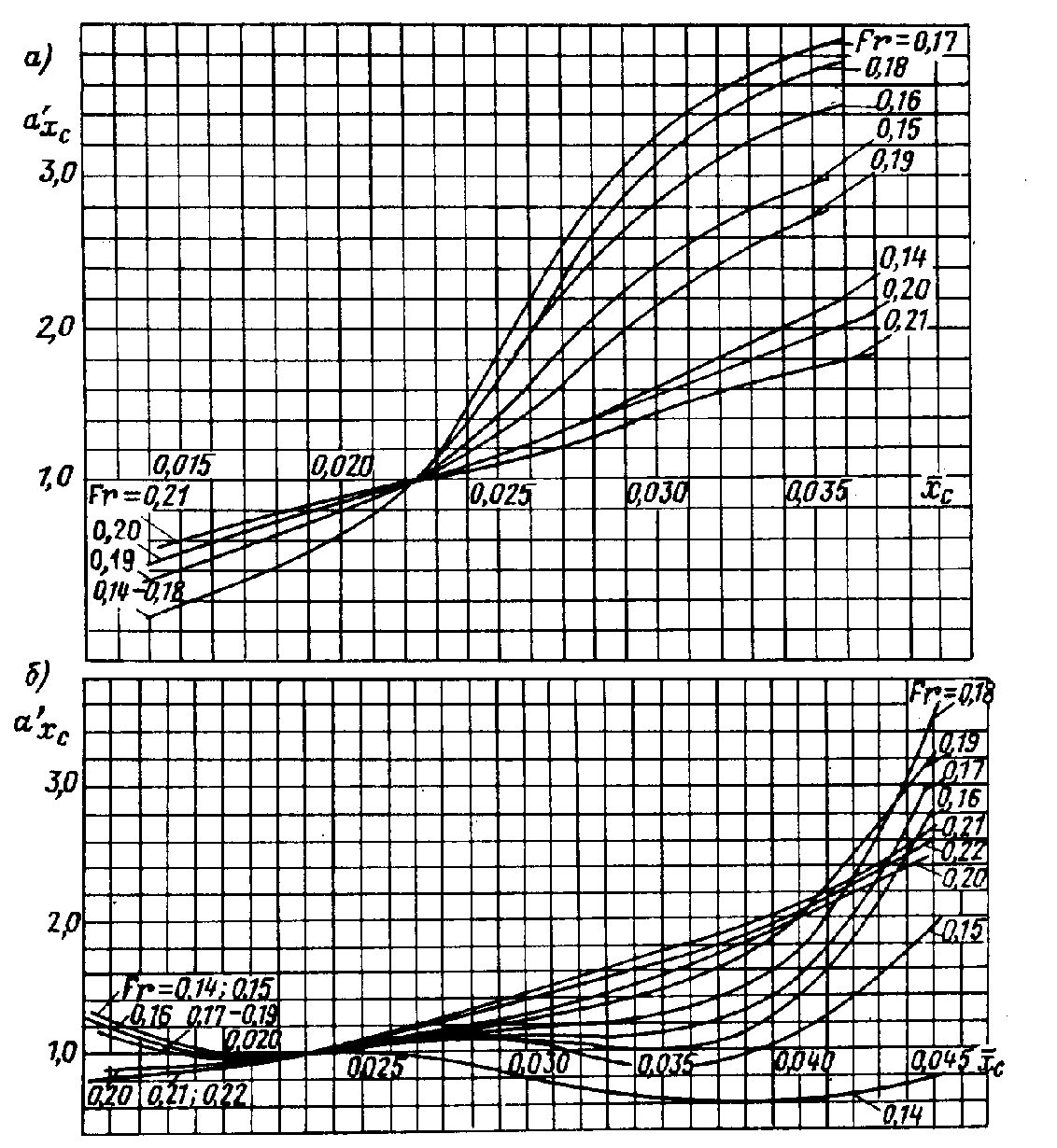
Рис. П.26. Зависимость
коэффициента влияния
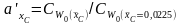 от
для носовых обводов: a
– с заострением ГВЛ ; b
– с притуплением ГВЛ
от
для носовых обводов: a
– с заострением ГВЛ ; b
– с притуплением ГВЛ
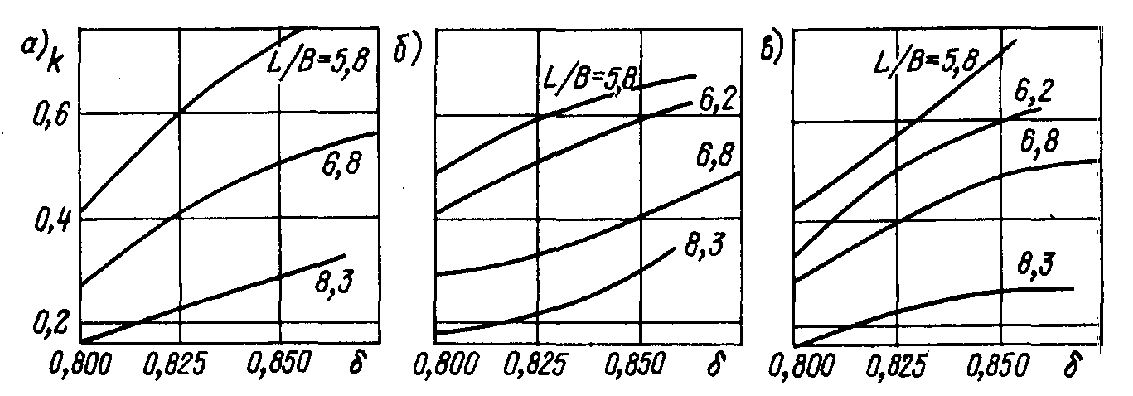
Рис. П.27. Зависимость
форм-фактора
и
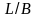 ;
а – цилиндрическая носовая оконечность;
б – бульбообразная носовая оконечность;
в – таранно-коническая носовая
оконечность.
;
а – цилиндрическая носовая оконечность;
б – бульбообразная носовая оконечность;
в – таранно-коническая носовая
оконечность.
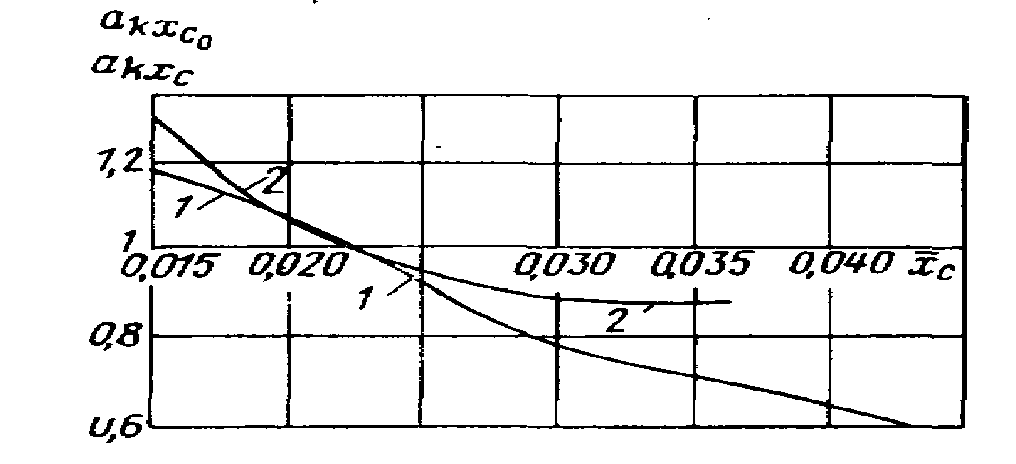
Рис. П.28. Зависимость
коэффициента влияния
 от
для различных типов носовых обводов.
от
для различных типов носовых обводов.
1 — носовые обводы с притуплением ГВЛ; 2 — носовые обводы с заострением ГВЛ.

Рис.П.29. Зависимость коэффициента влияния от для различных форм кормовой оконечности.
/ — V-образиая форма кормы; 2 — сигарообразная форма кормы.
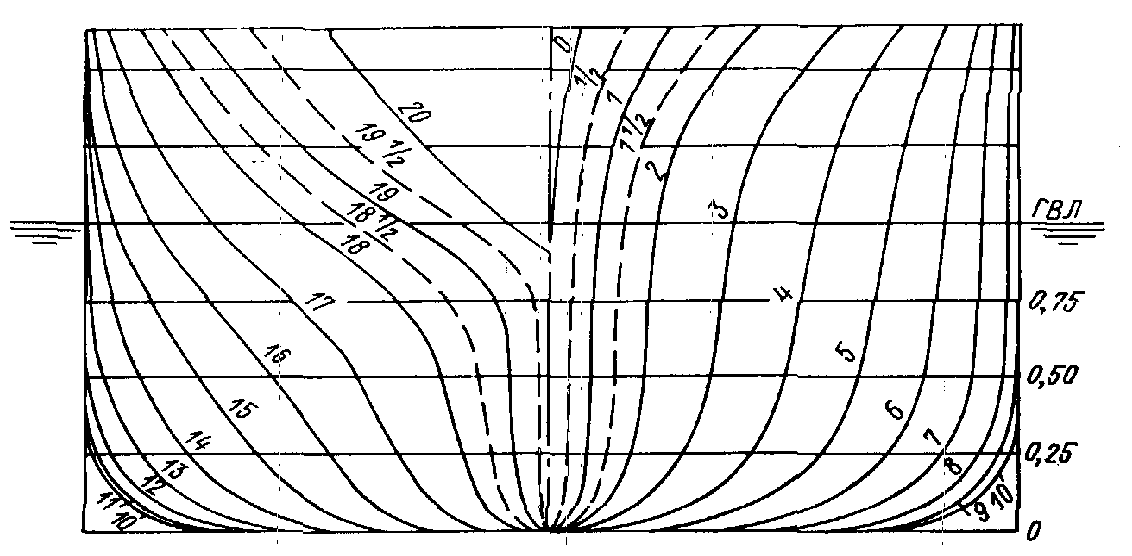
Рис.П.30. Теоретический корпус модели серии 60 (L/B=7,5; = 0,6).
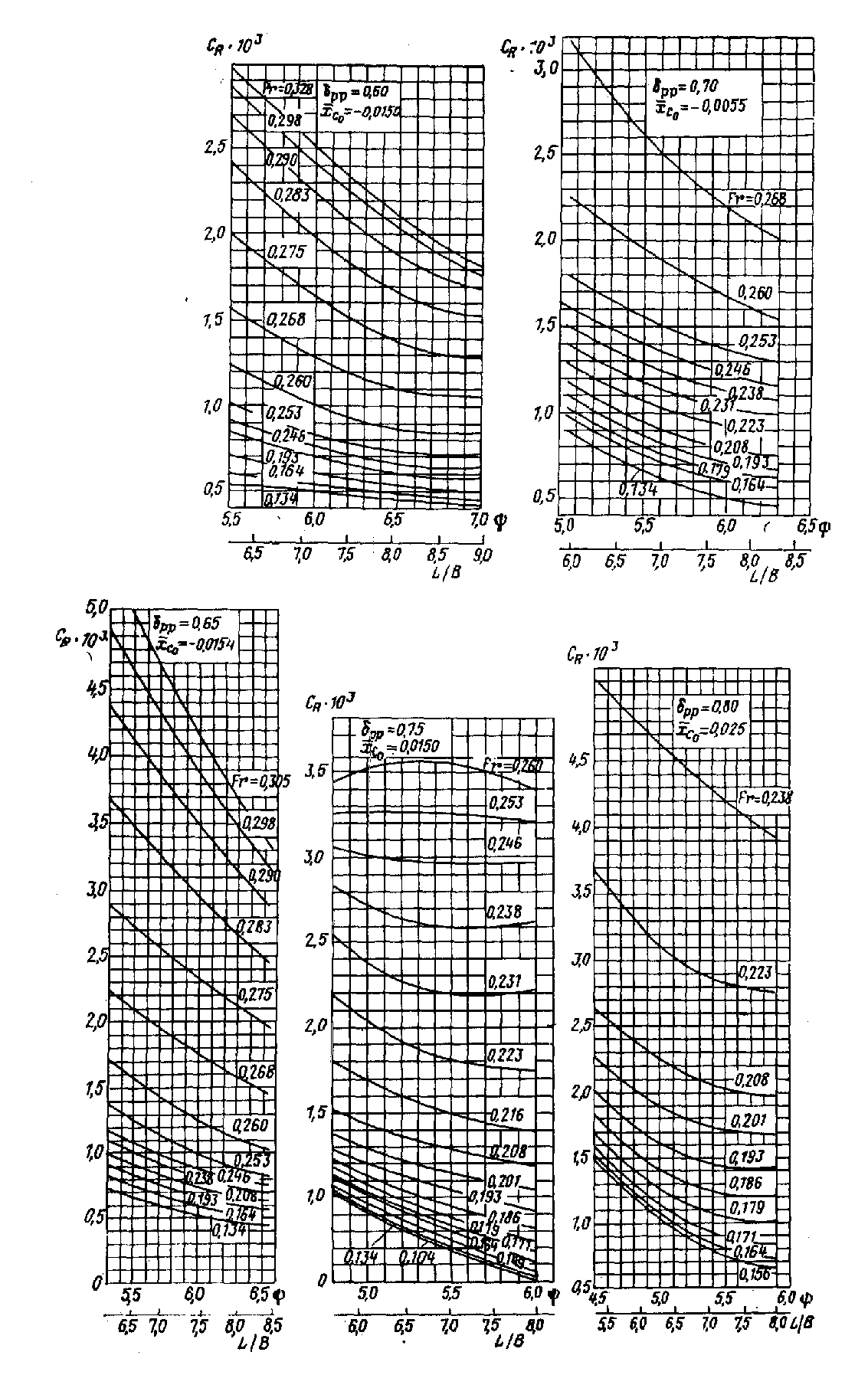 Рис.
П.31. Зависимости
от
и L/B
при различных значениях
и B/T=2,5.
Рис.
П.31. Зависимости
от
и L/B
при различных значениях
и B/T=2,5.
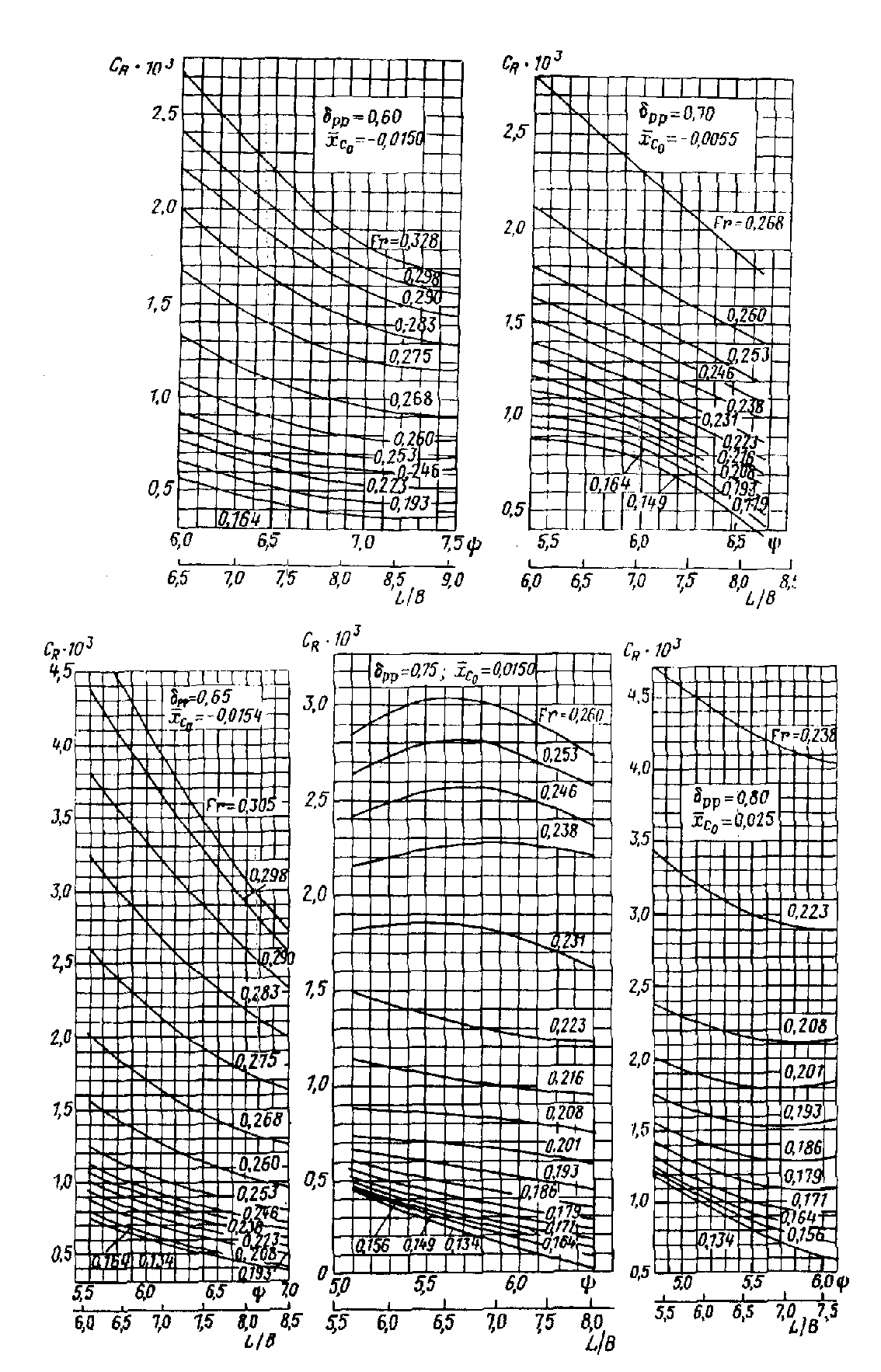
Рис. П.32. Зависимости от и L/B при различных значениях B/T=3,0.

Рис. П.33. Зависимость от и L/B при различных значениях B/T=3,5.
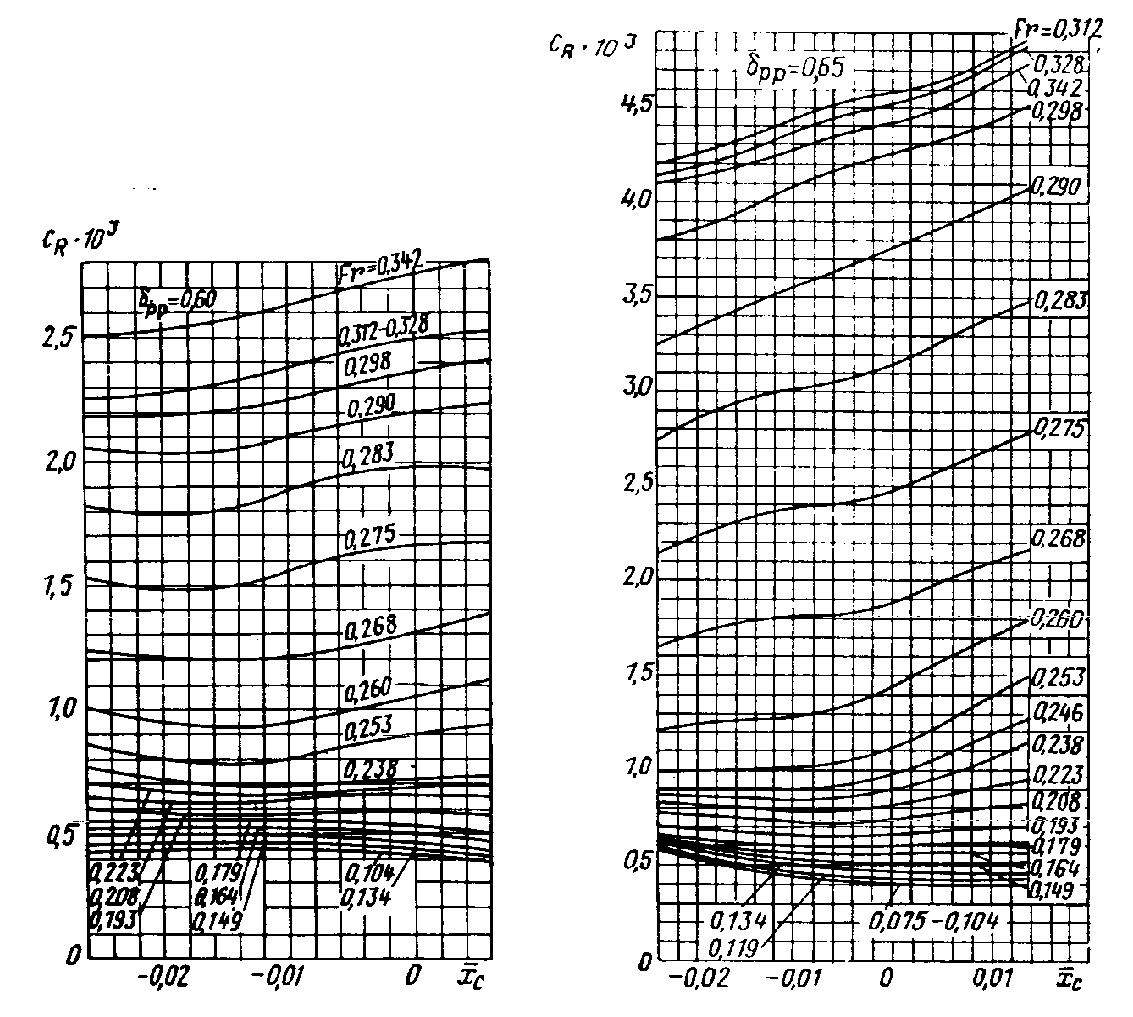
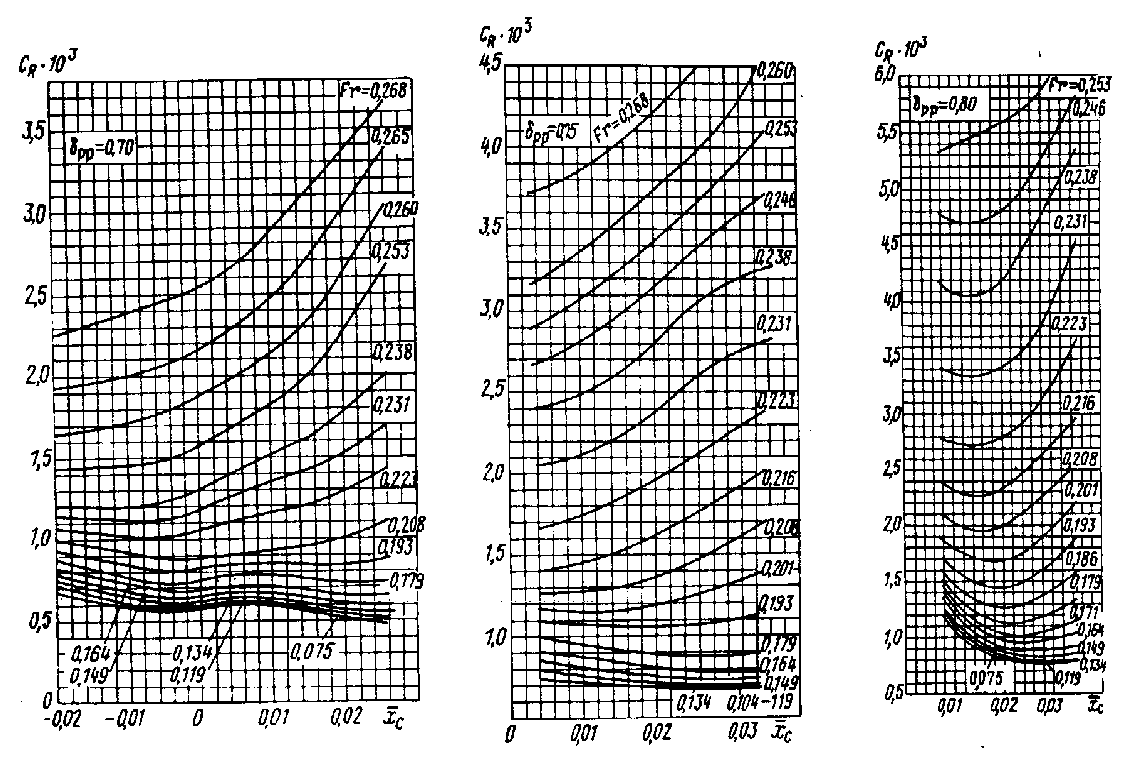
Рис. П.34. Зависимость от при различных значениях .
Серии рыбопромысловых судов. Первое отечественное систематическое исследование сопротивления и характеристик ходкости промысловых судов различных типов выполнено В. А. Ерошиным. Были испытаны модели трех серий: больших рыболовных траулеров, среднетоннажных [19] и малых [20] промысловых судов. Ниже в виду наибольшей перспективности приводятся материалы двух последних серий.
Исходные модели
серий среднетоннажных и малых промысловых
судов при различных значениях отношения
Lpp/B
имеют
одинаковую базовую форму обводов,
которая может быть охарактеризована
теоретическим корпусом, приведенным
на рис. П.35. В обеих сериях варьируются
одни и те же основные геометрические
параметры корпуса
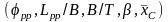 ,
однако пределы
их изменения
различны: в серии среднетоннажных
промысловых судов
,
однако пределы
их изменения
различны: в серии среднетоннажных
промысловых судов
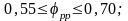
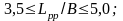
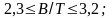
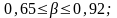
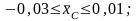 в серии малых промысловых судов
в серии малых промысловых судов
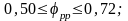
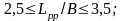
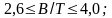
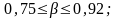
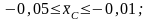 .
.
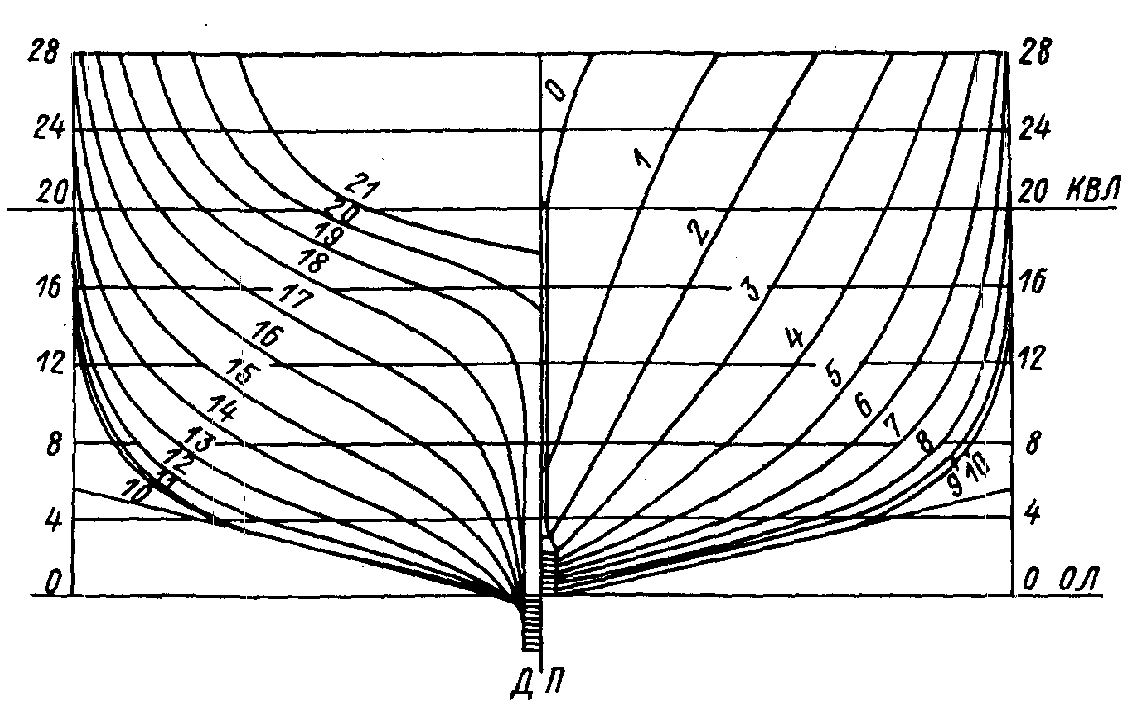
Рис. П.35. Теоретический корпус базовых моделей серий среднетоннажных и малых промысловых судов.

Рис.
П.36. Зависимость
от
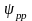 для промысловых судов: а – среднетоннажных;
б – малых.
для промысловых судов: а – среднетоннажных;
б – малых.
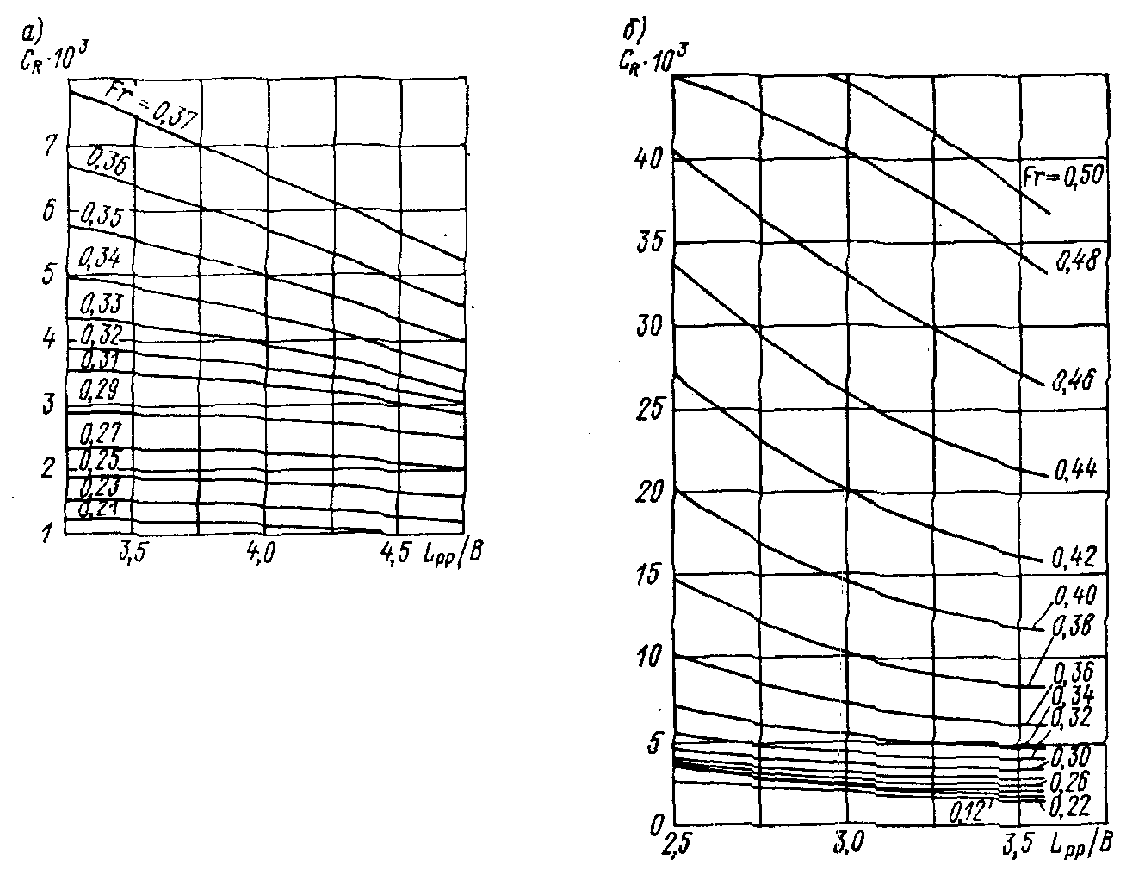
Рис. П.37. Зависимость от для промысловых судов: а – среднетоннажные; б – малых.
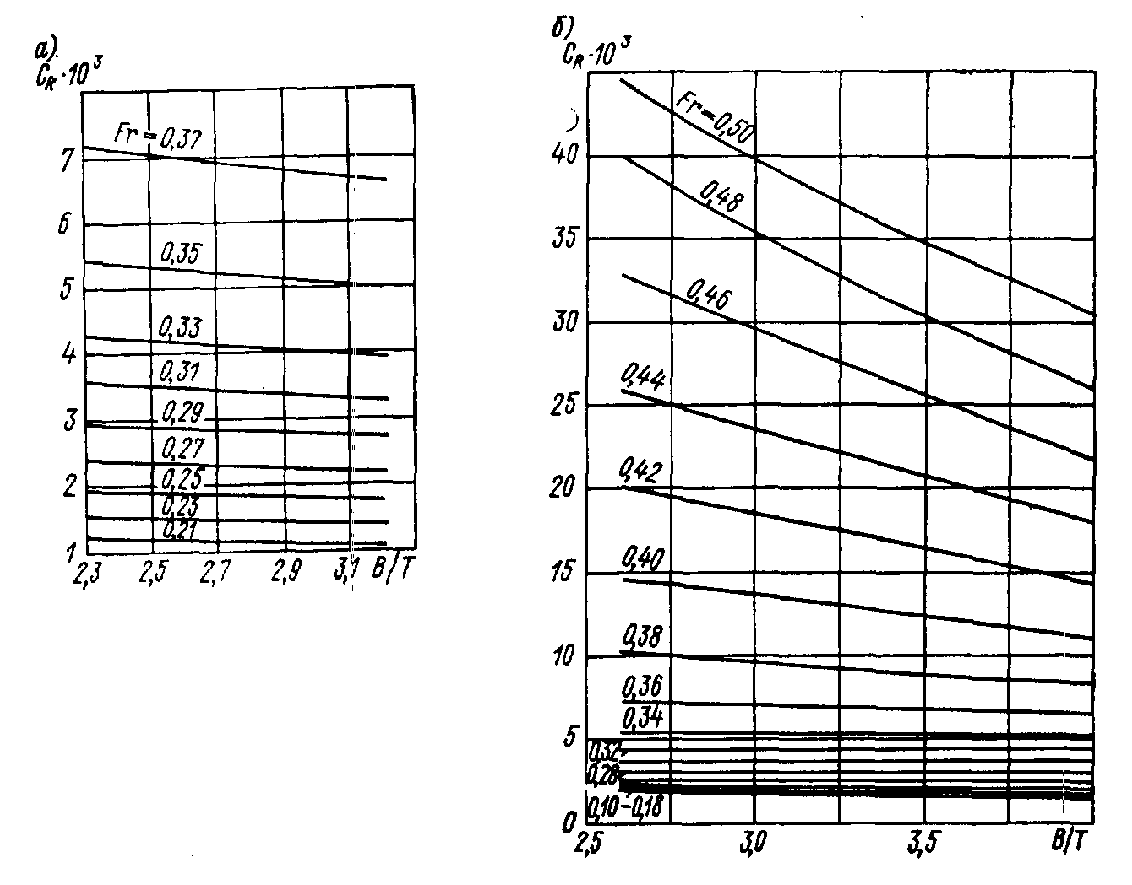
Рис.
П.38. Зависимость
от
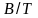 для промысловых судов: а – средне-тоннажные;
б – малых.
для промысловых судов: а – средне-тоннажные;
б – малых.
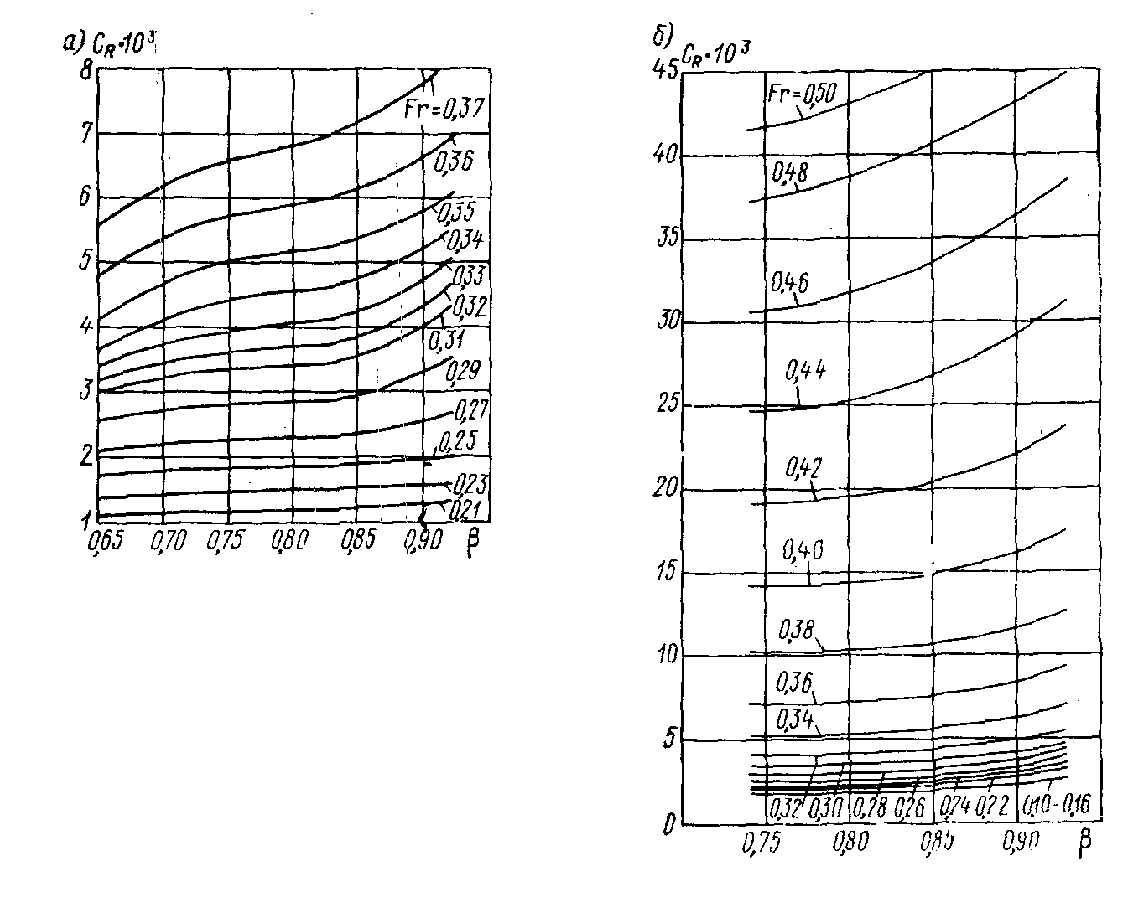
Рис. П.39. Зависимость от для промысловых судов: а – средне-тоннажные; б – малых.
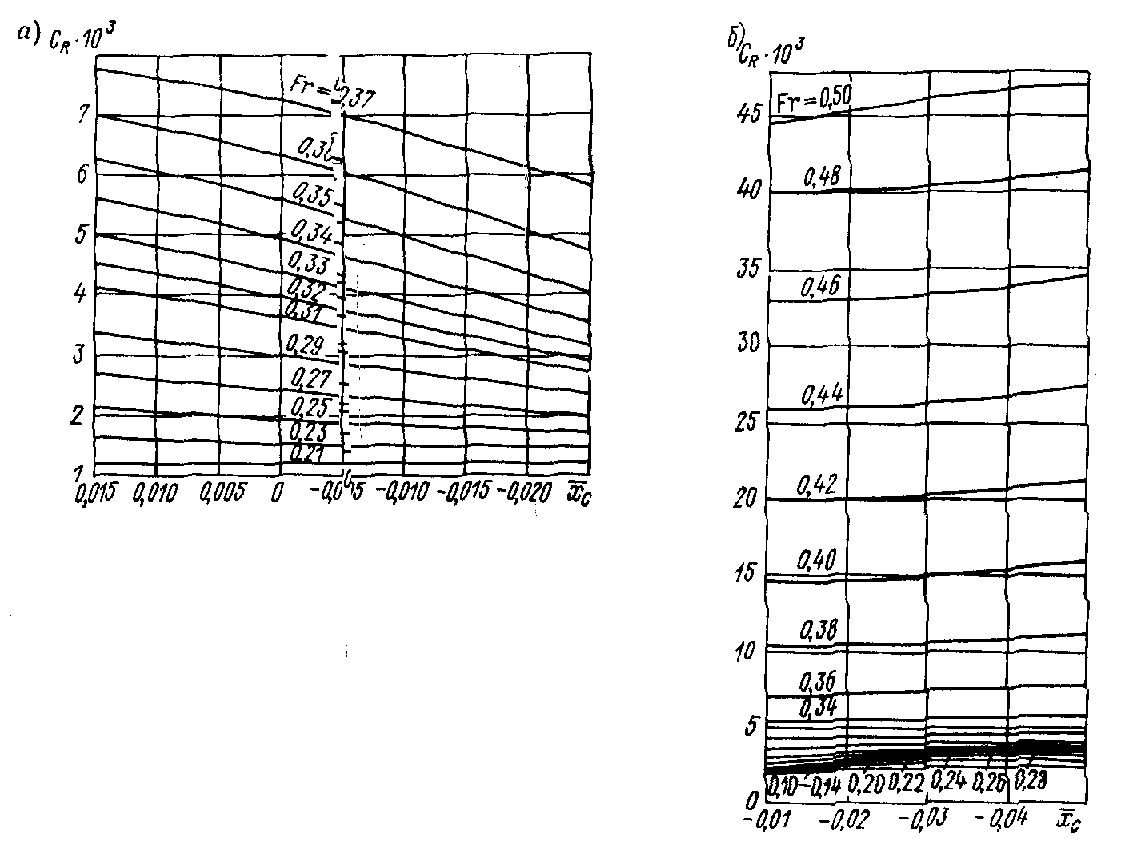
Рис. П.40. Зависимость от для промысловых судов: а – средне-тоннажные; б – малых.
Результаты буксировочных испытаний моделей серий в виде зависимости коэффициента от каждого варьируемого параметра при фиксированных базовых значениях остальных для среднетоннажных и малых судов приведены на рис. П.36-П.40. Такая форма представления результатов позволяет наглядно выявить характер влияния каждого геометрического параметра на , пользуясь зависимостью
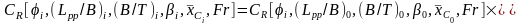
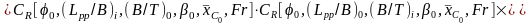
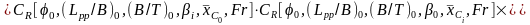
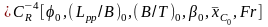 ,
,
где индексом “i” обозначены относительные геометрические параметры корпуса, для которого производится расчёт, а индексом «0» аналогичные параметры базовой формы корпуса.
В
качестве базовых в серии среднетоннажных
судов приняты:
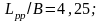
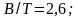

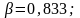
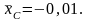 В серии малых промысловых судов базовая
форма обводов имеет отношение
В серии малых промысловых судов базовая
форма обводов имеет отношение
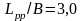 ;
остальные значения параметров те же,
что и в серии среднетоннажных судов.
;
остальные значения параметров те же,
что и в серии среднетоннажных судов.
Применение формулы (П.12) эквивалентно расчёту с введением коэффициентовь влияния на различие в значениях четырёх из пяти варьируемых параметров в каждой серии.

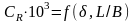 (см.
Рис. П.21,
а)
(см.
Рис. П.21,
а)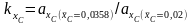 (см. Рис. П.25,
б)
(см. Рис. П.25,
б)