
- •Определение параметров модели продольного движения судна
- •Введение.
- •Задание
- •Часть 1. Геометрические характеристики
- •Часть 2. Водоизмещение и Коэффициенты полноты
- •Часть 3. Определение сопротивления движению судна на тихой воде
- •Часть 4. Определение аэродинамического сопротивления
- •Часть 5. Определение сопротивления руля
- •Часть 6. Определение дополнительного сопротивления на волнении
- •Часть 7. Определение присоединенных масс корпуса
- •Часть 8. Определение параметров гребного винта и сил от него
- •Список терминов, обозначений, сокращений
- •Способы приближенного определения остаточного сопротивления судна на основании серийных испытаний моделей
- •Серия судов полных обводов.
- •Пример выполнения задания
- •Список литературы
Список терминов, обозначений, сокращений
- Коэффициент общей полноты;
L -Длина по грузовой ватерлинии;
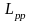 -
Длина между перпендикулярами
-
Длина между перпендикулярами
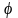 - Коэффициент
продольной полноты
- Коэффициент
продольной полноты
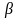 - Коэффициент
полноты мидель-шпангоута
- Коэффициент
полноты мидель-шпангоута
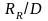 - Удельное остаточное
сопротивление;
- Удельное остаточное
сопротивление;
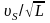 - Относительная
скорость;
- Относительная
скорость;
 - Коэффициент
остаточного сопротивления
- Коэффициент
остаточного сопротивления
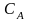 - Надбавка на
шероховатость
- Надбавка на
шероховатость
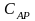 - Коэффициент
сопротивления выступающих частей
- Коэффициент
сопротивления выступающих частей
 - Коэффициент
сопротивления
- Коэффициент
сопротивления
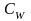 - Коэффициент
волнового сопротивления;
- Коэффициент
волнового сопротивления;
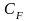 - Коэффициент
сопротивления трения
- Коэффициент
сопротивления трения
Fr – Число Фруда;
k – Коэффициент влияния формы тела на вязкостное сопротивление (формфактор);
- относительная длина судна
 - Скорость судна
в узлах;
- Скорость судна
в узлах;
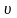 - Скорость судна
в метрах в секунду;
- Скорость судна
в метрах в секунду;
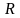 - Полное сопротивление
- Полное сопротивление
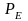 - буксировочная
мощность
- буксировочная
мощность
Приложение 2.
Способы приближенного определения остаточного сопротивления судна на основании серийных испытаний моделей
Серия быстроходных и среднескоростных судов. Для расчета сопротивления судов с низкими значениями коэффициента общей полноты могут быть использованы результаты испытаний моделей систематической серии Японской судостроительной исследовательской ассоциации и отечественной серии быстроходных и среднескоростных судов (табл. П.1). Отечественная серия предназначена для определения сопротивления судов с малыми и отношением L/B и большими значениями отношения В/Т, преимущественно контейнерных и грейдерных судов, в том числе с горизонтальным способом погрузки, а также лихтеровозов.
Приведенные
на рис. П. 1 чертежи корпуса и штевней
исходной модели серии выполнены
применительно к одновальному варианту
расположения движительного комплекса,
однако без изменения обводов «голого
корпуса» они могут быть использованы
и для двухвальных вариантов, что было
осуществлено при самоходных испытаниях
моделей серии. Основные геометрические
характеристики корпуса приведены в
табл. П.1. Продольное положение центра
величины
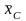 изменялось в пределах
= —0,0250,028
для V-образных носовых обводов и
= —0,0170,020
для бульбовых, смещаясь в корму с
уменьшением коэффициента .
изменялось в пределах
= —0,0250,028
для V-образных носовых обводов и
= —0,0170,020
для бульбовых, смещаясь в корму с
уменьшением коэффициента .
При расчете сопротивления судна по материалам данной серии с использованием традиционной схемы разделения сопротивления на составляющие коэффициент остаточного сопротивления определяется по формуле
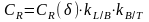 (П.2)
(П.2)
Коэффициент
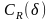 снимается
с рис. П.2 или П.3 в зависимости от формы
носовой оконечности. Коэффициент влияния
несоответствия отношения L/B
определяется из рис. П.4 или П.5 как
отношение значений коэффициента
для
расчетного значения L/B
и стандартного
L/B =
5,64;
снимается
с рис. П.2 или П.3 в зависимости от формы
носовой оконечности. Коэффициент влияния
несоответствия отношения L/B
определяется из рис. П.4 или П.5 как
отношение значений коэффициента
для
расчетного значения L/B
и стандартного
L/B =
5,64;
![]() .
.
Коэффициент
влияния
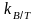 ,
учитывающий несоответствие расчетного
и стандартного значений B/T
= 3.5,
непосредственно снимается с диаграммы
рис. П.6.
,
учитывающий несоответствие расчетного
и стандартного значений B/T
= 3.5,
непосредственно снимается с диаграммы
рис. П.6.
Результаты
испытаний моделей серии могут быть
использованы и для расчета сопротивления
но схеме, основанной на физических
принципах разделения на составляющие.
В этом случае коэффициент расчетного
полнового сопротивления
 в зависимости (VI.16) определяется но
формуле
в зависимости (VI.16) определяется но
формуле
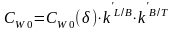 (П.3)
(П.3)
Коэффициент
снимается с рис. П.2 или П.3 как разность
значений коэффициентов
,
соответствующих расчетному Fr
и минимальному на графике значению Fr =
0,17:

.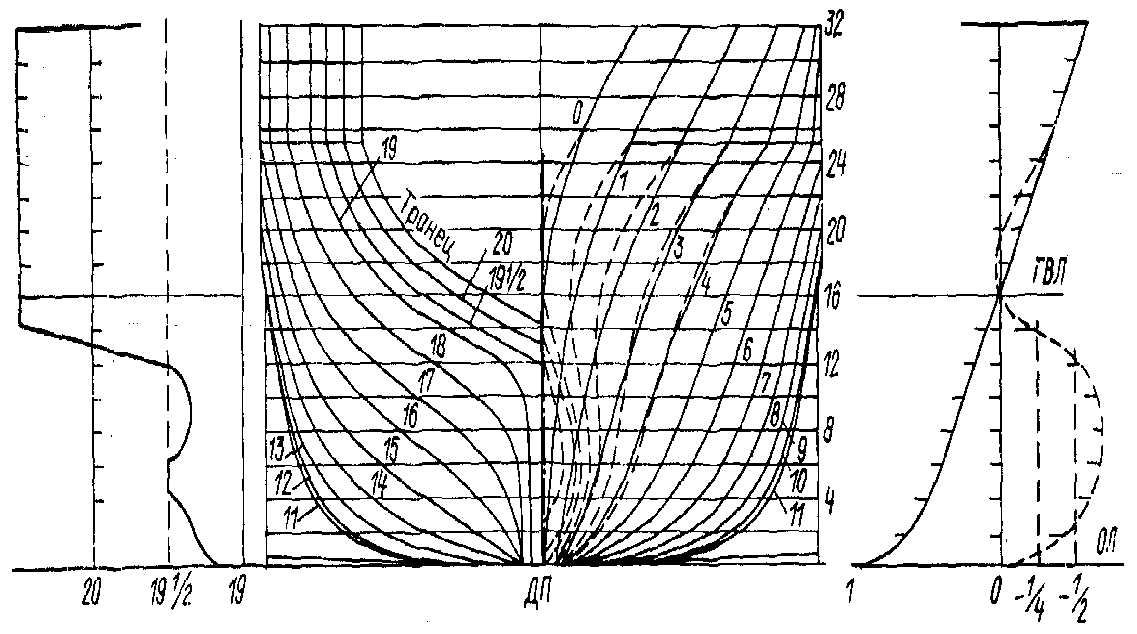
Рис. П.1. Теоретический корпус и штевни исходной модели серии быстроходных и среднескоростных судов. - V-образная носовая оконечность; - бульбообразная носовая оконечность.
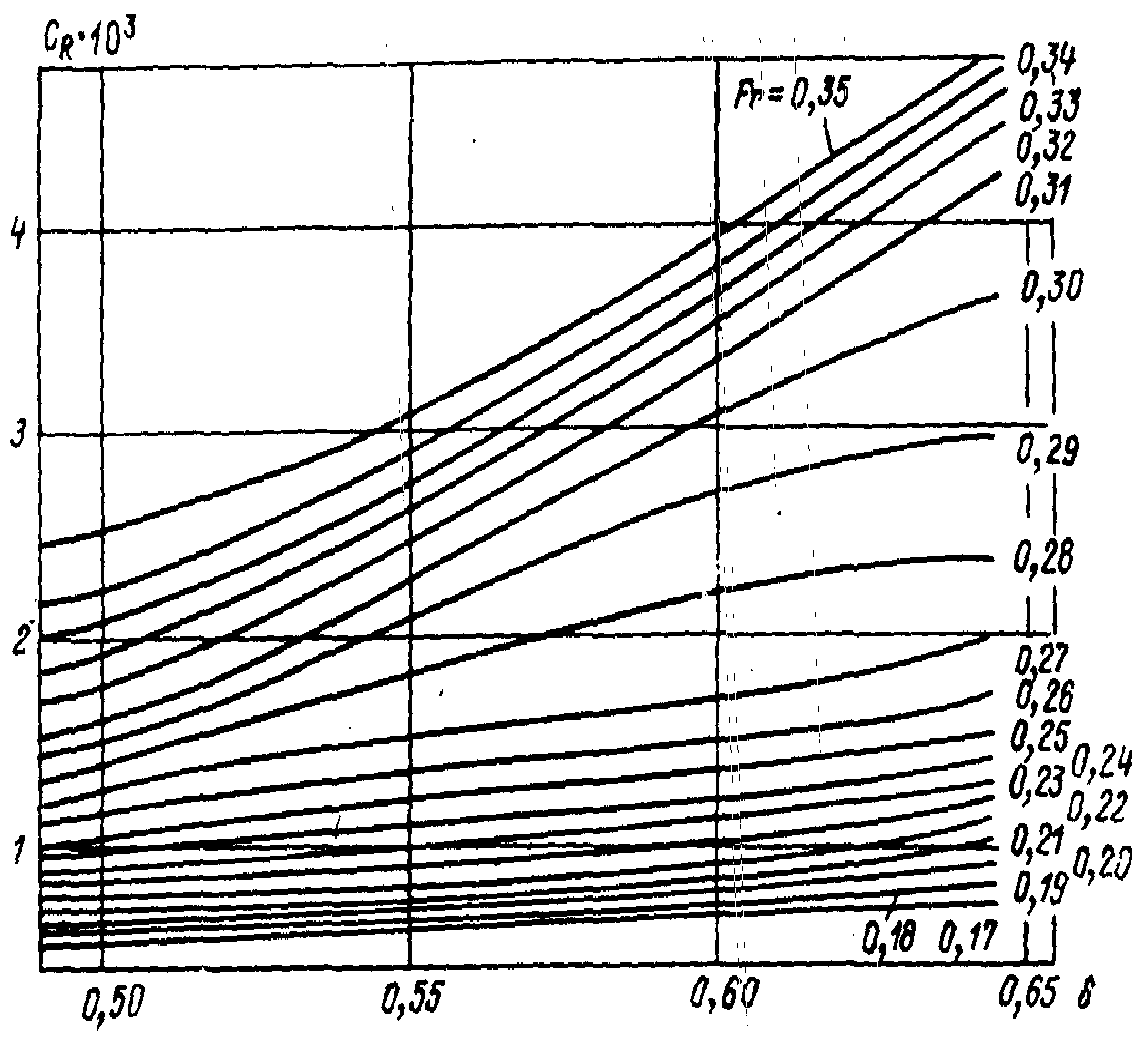
Рис. П.2. зависимость от для судов с V-образной носовой оконечностью (L/B = 5,64; B/T = 3,5).
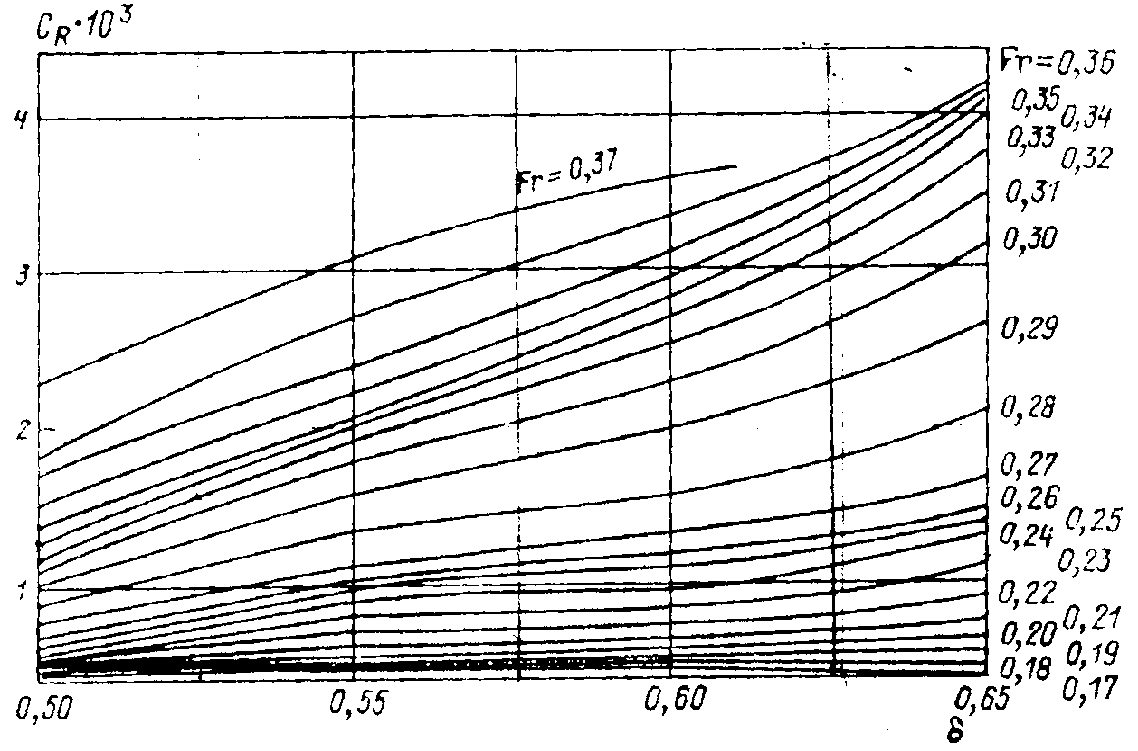
Рис. П.3. Зависимость от для судов с бульбообразной носовой оконечностью (L/B = 5,64; B/T = 3,5).
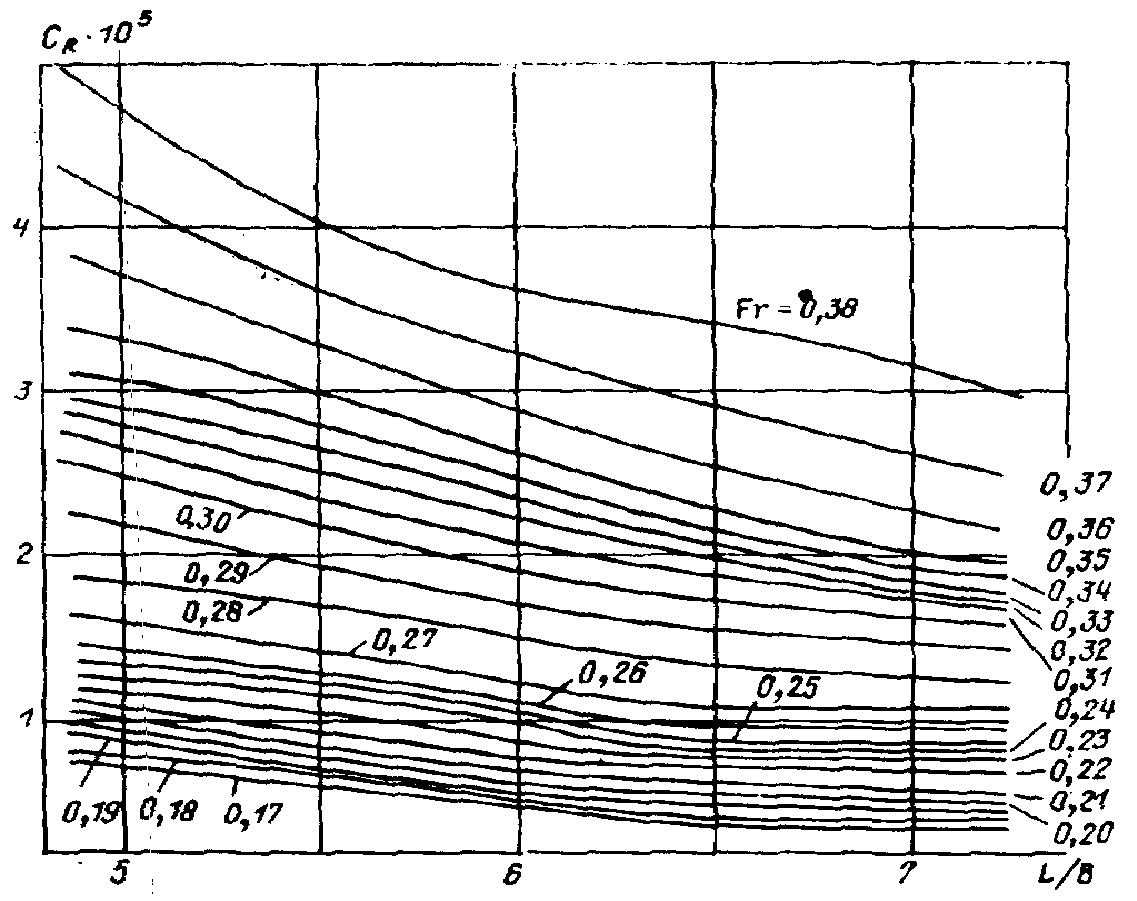
Рис. П.4. Зависимость от L/B для судов с V-образной носовой оконечностью (B/T = 3,5).
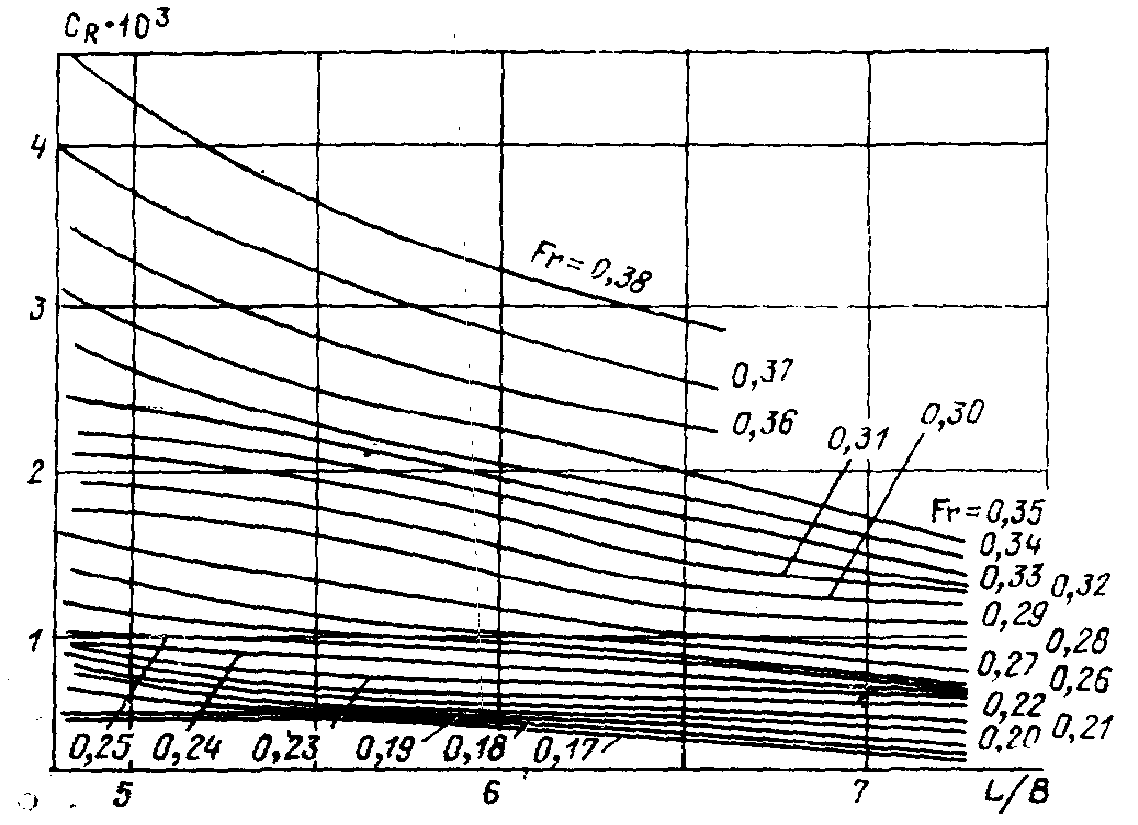
Рис. П.5. Зависимость от L/B для судов с бульбообразной носовой оконечностью (B/T = 3,5).
Коэффициент
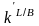 рассчитывается
как отношение коэффициентов
для расчетного LIB
и стандартного L/B
= 5,64,
определенных по графикам рис. П.4 или
П.5, аналогично определению коэффициента
рассчитывается
как отношение коэффициентов
для расчетного LIB
и стандартного L/B
= 5,64,
определенных по графикам рис. П.4 или
П.5, аналогично определению коэффициента
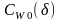 :
:
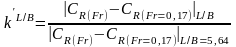
Коэффициент
влияния
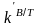 снимается с графика на рис. П.7. При
определении сопротивления в
соответствии с зависимостью (VI.16)
коэффициент влияния формы корпуса на
вязкостное сопротивление k
рассчитывается по формуле
снимается с графика на рис. П.7. При
определении сопротивления в
соответствии с зависимостью (VI.16)
коэффициент влияния формы корпуса на
вязкостное сопротивление k
рассчитывается по формуле
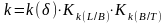 (П.4)
(П.4)
При
этом k()
определяется
по рис. П.8 в зависимости от формы носовой
оконечности. Коэффициент
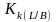 рассчитывается как отношение значений
форм-фактора k
для расчетного
значения
LIB
и стандартного L/В
= 5,64:
рассчитывается как отношение значений
форм-фактора k
для расчетного
значения
LIB
и стандартного L/В
= 5,64:
 ,
снимаемых с графика на рис. П.9. Коэффициент
,
снимаемых с графика на рис. П.9. Коэффициент
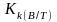 вычисляется
аналогичным образом как
вычисляется
аналогичным образом как
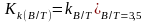 значениям k,
определяемым
из рис. П.10 при расчетном значении L/B.
значениям k,
определяемым
из рис. П.10 при расчетном значении L/B.
В качестве примера в табл. П.1 выполнен расчет буксировочной мощности судна с горизонтальным способом погрузки со следующими основными элементами:
L
= 128,7 м; L/B
= 6,71; В/Т
= 3,2;
= 0,604;
= 2726
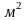 и V-образными носовыми обводами. Здесь
и в последующих примерах
= 1026 кг/м3.
и V-образными носовыми обводами. Здесь
и в последующих примерах
= 1026 кг/м3.
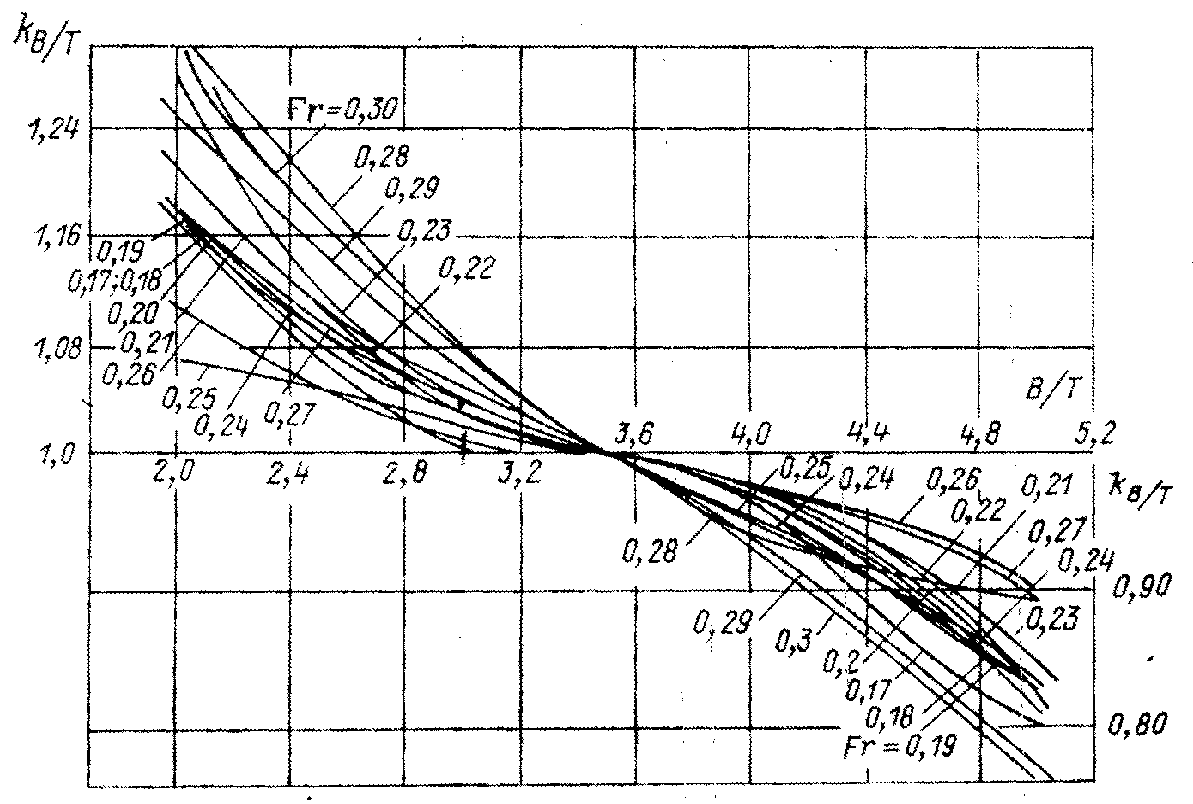
Рис.
П.6. Зависимость коэффициента влияния
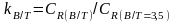 от B/T.
от B/T.
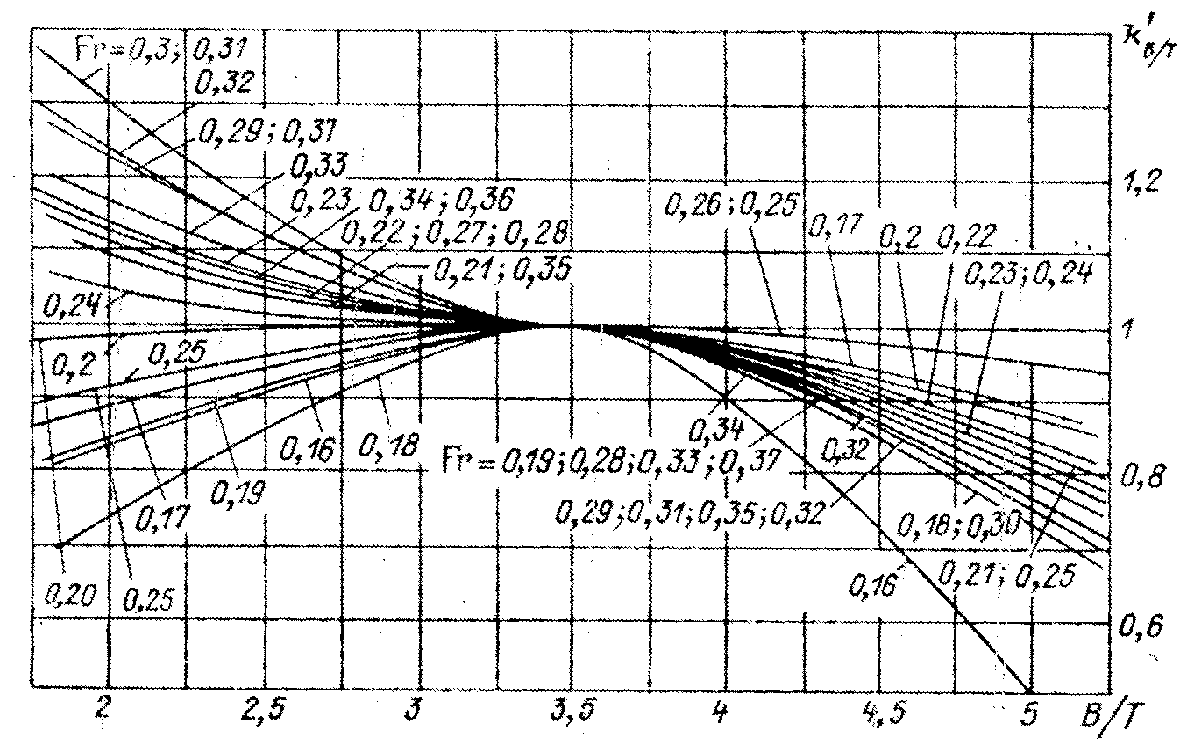
Рис.
П.7. Зависимость коэффициента влияния
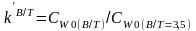 от B/T.
от B/T.
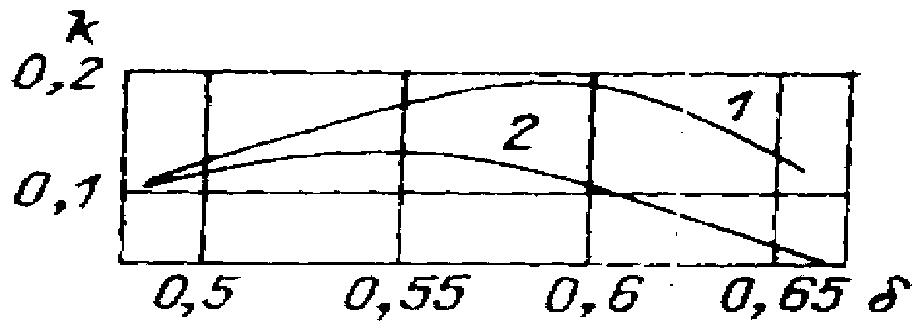
Рис. П.8. Зависимость формфактора k от (L/B = 5,64; B/T = 3,5).
1 - V-образчая носовая оконечность; 2 - бульбообразная носовая оконечность.
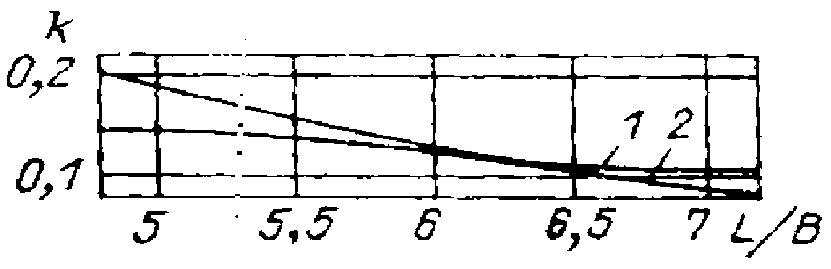
Рис. П.9. Зависимость формфактора k от L/B (В/Т = 3,5).
1 - V-образная носовая оконечность; 2 - бульбообразная носовая оконечность.
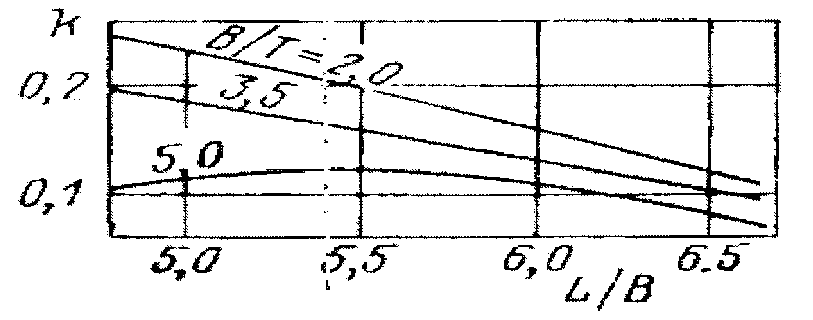
Рис. П.10. Зависимость k от отношений L/B и B/T.
Таблица П.1. Расчет буксировочной мощности по материалам серии быстроходных и среднескоростных судов
№ п/п. |
Обозначение расчетных величин |
Численные значения |
|||||
1 |
|
13 |
14 |
15 |
16 |
17 |
18 |
2 |
|
6,70 |
7,20 |
7,73 |
8,24 |
8,75 |
9,27 |
3 |
|
44,89 |
51,84 |
59,60 |
67,90 |
76,56 |
85,93 |
4 |
|
0,190 |
0,202 |
0,218 |
0,232 |
0,248 |
0,262 |
5 |
|
0,790 |
0,840 |
0,980 |
1,170 |
1,360 |
1,550 |
6 |
|
0,705 |
0,703 |
0,778 |
0.776 |
0,745 |
0,774 |
7 |
|
1,018 |
1,020 |
1,019 |
1,022 |
1,012 |
1,003 |
8 |
|
0,567 |
0,602 |
0,777 |
0,928 |
1,025 |
1,203 |
9 |
|
5,356 |
5,756 |
6,179 |
6,587 |
6,995 |
7,410 |
10 |
|
1,699 |
1,684 |
1,668 |
1,654 |
1,642 |
1,630 |
11 |
|
0,30 |
0,30 |
0,30 |
0,30 |
0,30 |
0,30 |
12 |
|
0,15 |
0,15 |
0,15 |
0,15 |
0,15 |
0,15 |
13 |
|
2,716 |
2,736 |
2,895 |
3,032 |
3,117 |
3,283 |
14 |
|
171,04 |
198,24 |
241,55 |
288,96 |
334,98 |
394,38 |
15 |
|
1146 |
1427 |
1867 |
2381 |
2931 |
3656 |
Серия судов с умеренной полнотой обводов. Область значений коэффициента = 0,600,80 охватывает большую часть морских транспортных судов различных типов и назначения, включая универсальные сухогрузные суда, среднетоннажные танкеры и рудовозы, суда для каботажных перевозок, а также транспортные суда флота рыбной промышленности. Для расчета сопротивления указанных судов могут быть применены материалы 60-й серии и серий. BSRA (табл. П.1, п. 1, 7). Тем же целям отвечает комплекс отечественных систематических серий (табл. П.1, п. 2), известный под названием «Серия морских транспортных судов» [12]. Указанный комплекс серий можно условно подразделить на основную серию (вариация соотношений главных размерений и коэффициента ) и ряд вспомогательных серий, охватывающих изменение геометрических характеристик формы обводов корпуса. Основные геометрические характеристики моделей названных серий приведены в табл. П.1. Изменение в зависимости от : = -(0,025—0,005) при =0,60,
= -0,005+0,015 при = 0,70 и = +0,01+0,03 при = 0,80. Изменение относительной длины составляло = L/V113 = 5,007,50. Формы носовых шпангоутов: U-образные, промежуточные и V-образные.
Форма обводов моделей серии иллюстрируется рис. П.11 (=0,70). При частичном использовании результатов испытаний моделей серий по традиционной схеме Фруда (VI.12) рассчитывается по формуле
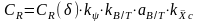 (П.5)
(П.5)
Коэффициент
снимается с диаграммы рис. П.12. Коэффициент
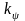 ,
учитывающий
влияние относительной длины
= L/V1/3,
вычисляется как
,
учитывающий
влияние относительной длины
= L/V1/3,
вычисляется как
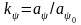 -
отношение значений коэффициента
-
отношение значений коэффициента
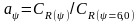 снимаемых с диаграммы рис. П.13 соответственно
для расчетного значения относительной
длины
и стандартного значения
снимаемых с диаграммы рис. П.13 соответственно
для расчетного значения относительной
длины
и стандартного значения
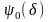 ,
определяемого из рис. П.12. Коэффициенты
и
,
определяемого из рис. П.12. Коэффициенты
и
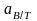 ,
произведение
которых учитывает влияние отличия
расчетного значения В/Т
от принятого в серии (B/T
= 2,5),
определяются по графику на рис. П.14.
Коэффициент
,
произведение
которых учитывает влияние отличия
расчетного значения В/Т
от принятого в серии (B/T
= 2,5),
определяются по графику на рис. П.14.
Коэффициент
 ,
учитывающий влияние на
различий между расчетными значениями
и стандартными
,
учитывающий влияние на
различий между расчетными значениями
и стандартными
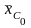 (
=
— 0,015 для
= 0,60;
=
0,005 для
= 0,70;
=
0,02 для
= 0,80)
(
=
— 0,015 для
= 0,60;
=
0,005 для
= 0,70;
=
0,02 для
= 0,80)
 ,
,
снимается с графиков рис. П.15. Выбор соответствующего графика определяется расчетным значением коэффициента .
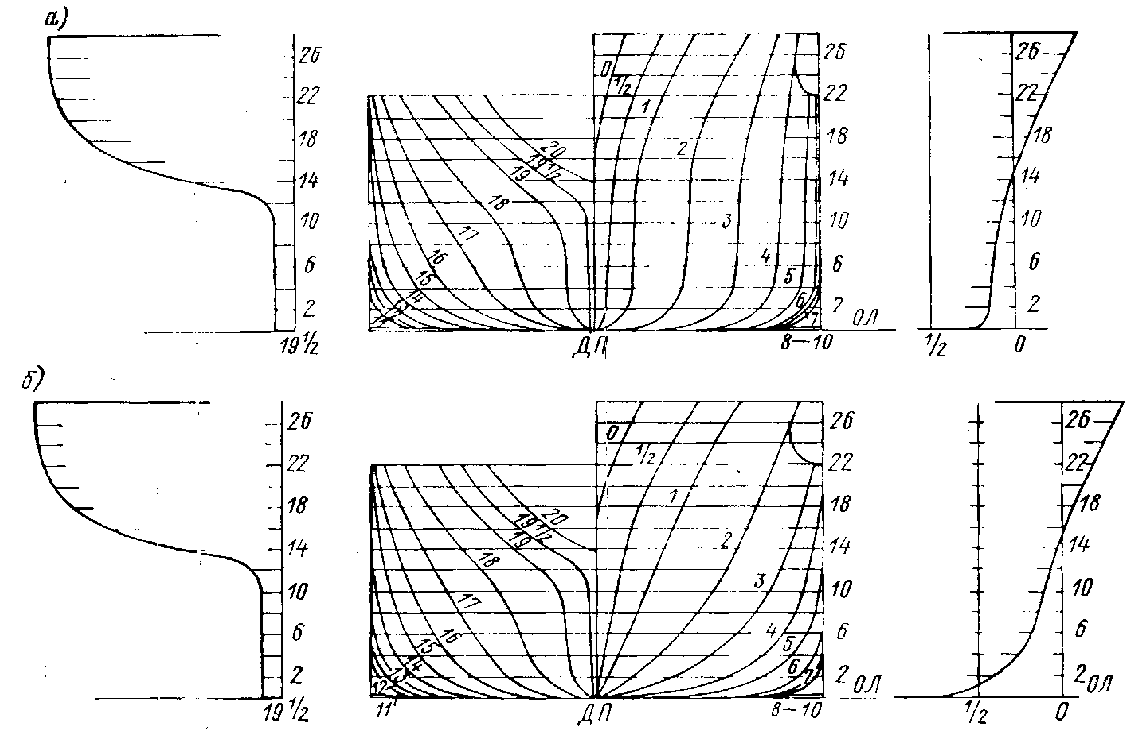
Рис. П.11. Теоретический корпус и штевни моделей серии универсальных морских транспортных судов (6 = 0,70): а — U-образная носовая оконечность; б — V-об-разная носовая оконечность.
Рис.
П. 12. Зависимость коэффициента остаточного
сопротивления я стандартных значений
относительной длины
 от
от
 (В/Т = 2,5).
(В/Т = 2,5).
По результатам испытаний моделей серии универсальных транспортных судов можно произвести приближенный расчет сопротивления при разделении его на физические составляющие согласно (VI. 16). В этом случае коэффициент Cwo определяется по формуле
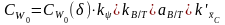 (VI
1.6)
(VI
1.6)
Коэффициент Cwo( ) вычисляется как разность значений коэффициентов , снимаемых с графика на рис. П.12 для расчетного числа Fr и минимального на диаграмме Fr = 0,100,15:

Коэффициенты
и
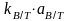 определяются по графикам рис. П.13 и П.14
аналогично расчету по формуле (П.5). Для
нахождения поправочного коэффициента
определяются по графикам рис. П.13 и П.14
аналогично расчету по формуле (П.5). Для
нахождения поправочного коэффициента
 на несоответствие в значениях
служат диаграммы на рис. П. 16, каждая из
которых относится к соответствующему
значению коэффициента
.
на несоответствие в значениях
служат диаграммы на рис. П. 16, каждая из
которых относится к соответствующему
значению коэффициента
.
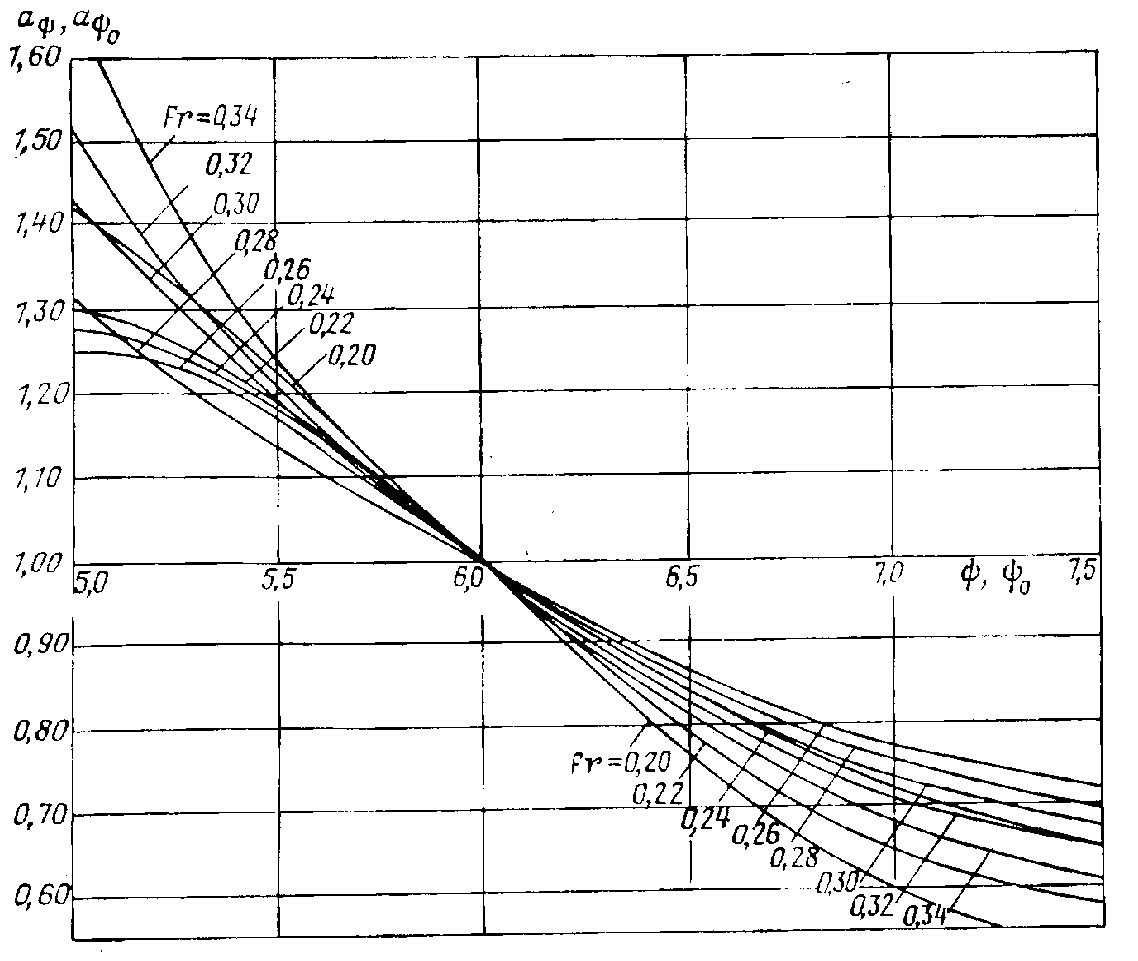
Рис.
П.13. Зависимость коэффициента влияния
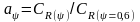 от .
от .
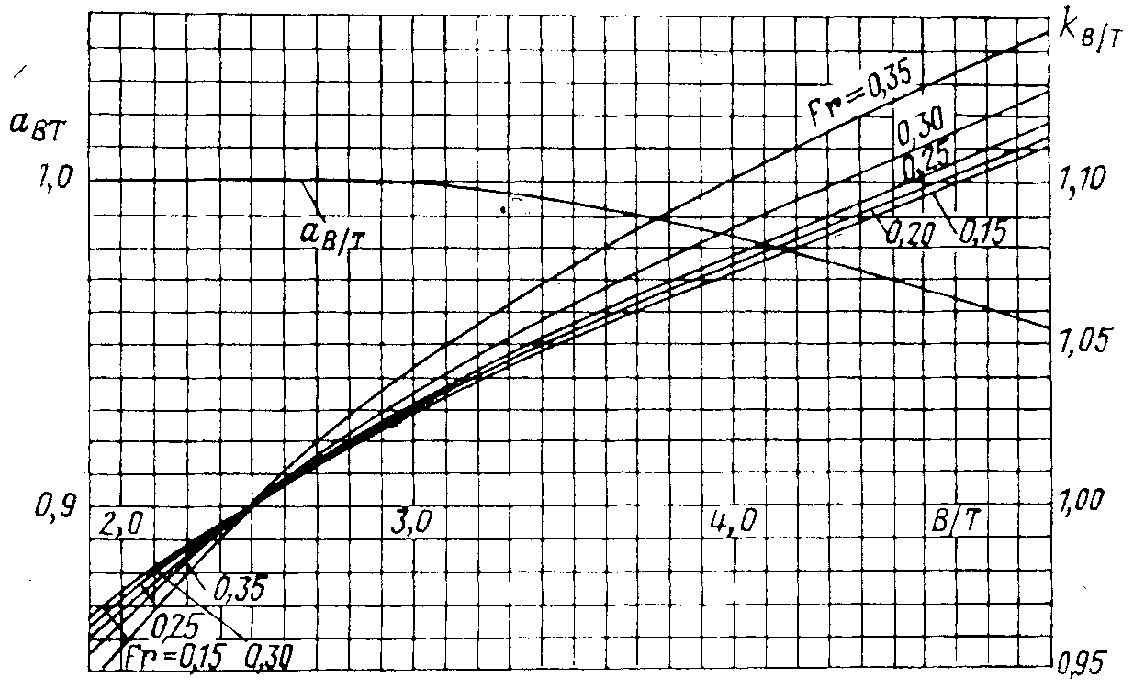
Рис. П.14. Зависимость коэффициентов влияния и от B/T.
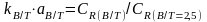
Коэффициент влияния формы корпуса на вязкостное сопротивление k рассчитывается по формуле

где
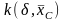 определяется по графику на рис. П.17
интерполяцией по коэффициенту
между кривыми
= const.
Поправочные коэффициенты
и
определяется по графику на рис. П.17
интерполяцией по коэффициенту
между кривыми
= const.
Поправочные коэффициенты
и
 снимаются с графиков на рис. П.13 и П.14
соответственно, также как при расчете
по формуле (П.5).
снимаются с графиков на рис. П.13 и П.14
соответственно, также как при расчете
по формуле (П.5).
В
приведенном выше способе расчета
сопротивления по материалам отечественной
систематической серии опущены диаграммы,
позволяющие учесть влияние коэффициента
вертикальной полноты носовой оконечности
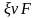 (формы носовых шпангоутов). Это
представлялось возможным ввиду более
слабого влияния последнего на
по сравнению с другими варьируемыми
характеристиками. Предполагается,
что зависимости поправочного множителя
.
(формы носовых шпангоутов). Это
представлялось возможным ввиду более
слабого влияния последнего на
по сравнению с другими варьируемыми
характеристиками. Предполагается,
что зависимости поправочного множителя
.
 от
,
построенные для моделей с U-образными
шпангоутами, остаются в силе и для других
обводов носовой оконечности. Полный
комплект диаграмм и схема расчета,
позволяющие учесть совместное влияние
на сопротивление
и
,
приведены
в [l2].
от
,
построенные для моделей с U-образными
шпангоутами, остаются в силе и для других
обводов носовой оконечности. Полный
комплект диаграмм и схема расчета,
позволяющие учесть совместное влияние
на сопротивление
и
,
приведены
в [l2].
В качестве примера в табл. П.2 выполнен расчет буксировочной мощности рыбопромысловой базы со следующими основными элементами: L = 186,5 м; LIB = 7,18; BIT = 3,34; = 6,25; = 1,4 %Lpp; = 0,725; = 5780 м2; и умеренно U-образными носовыми обводами.
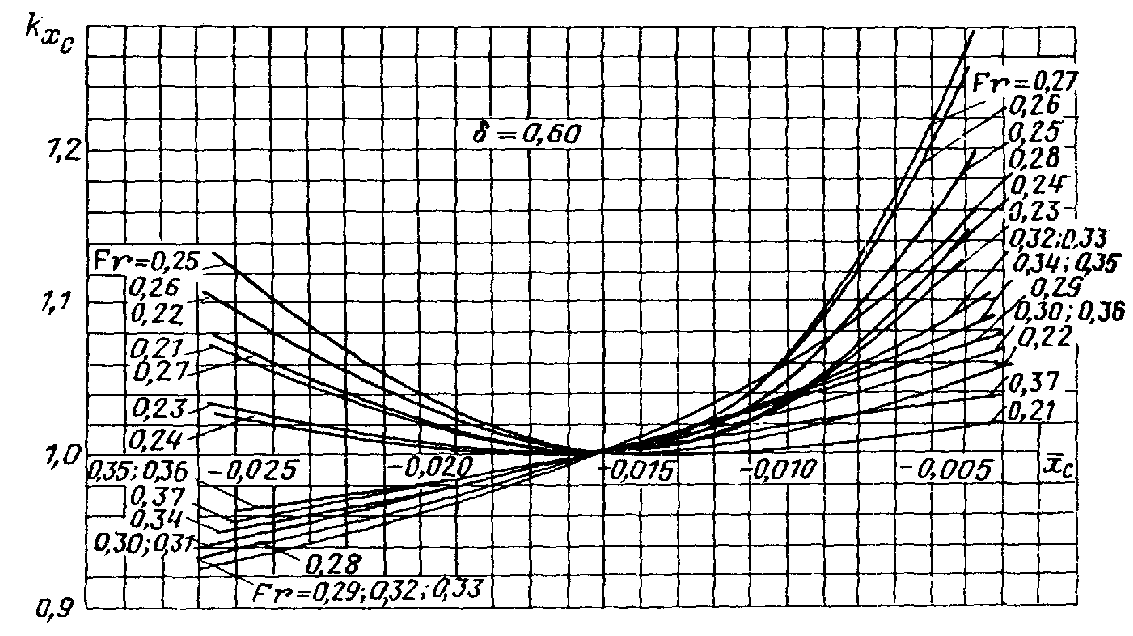
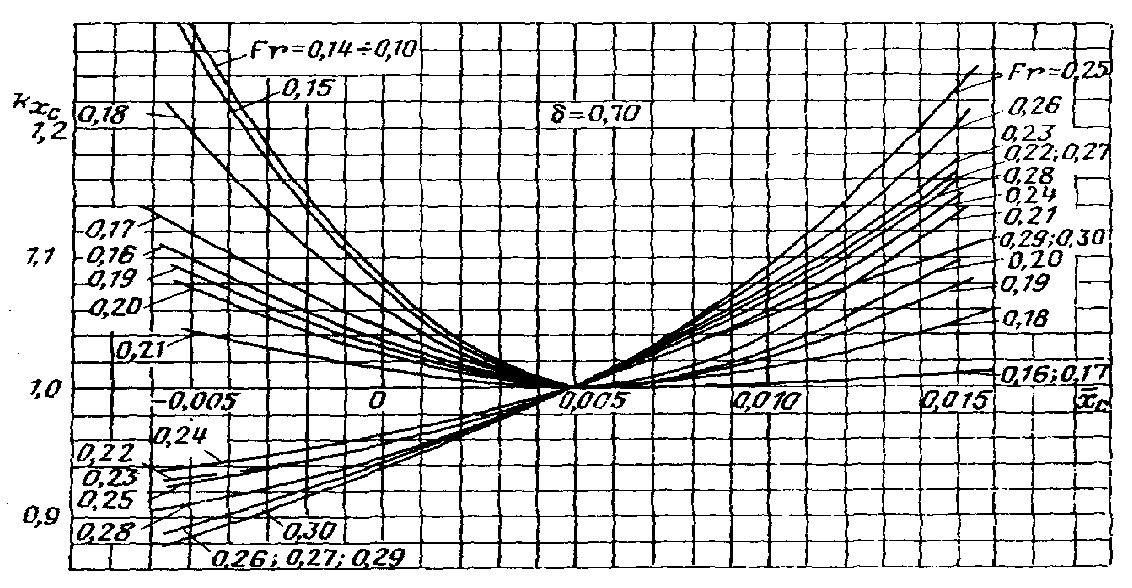
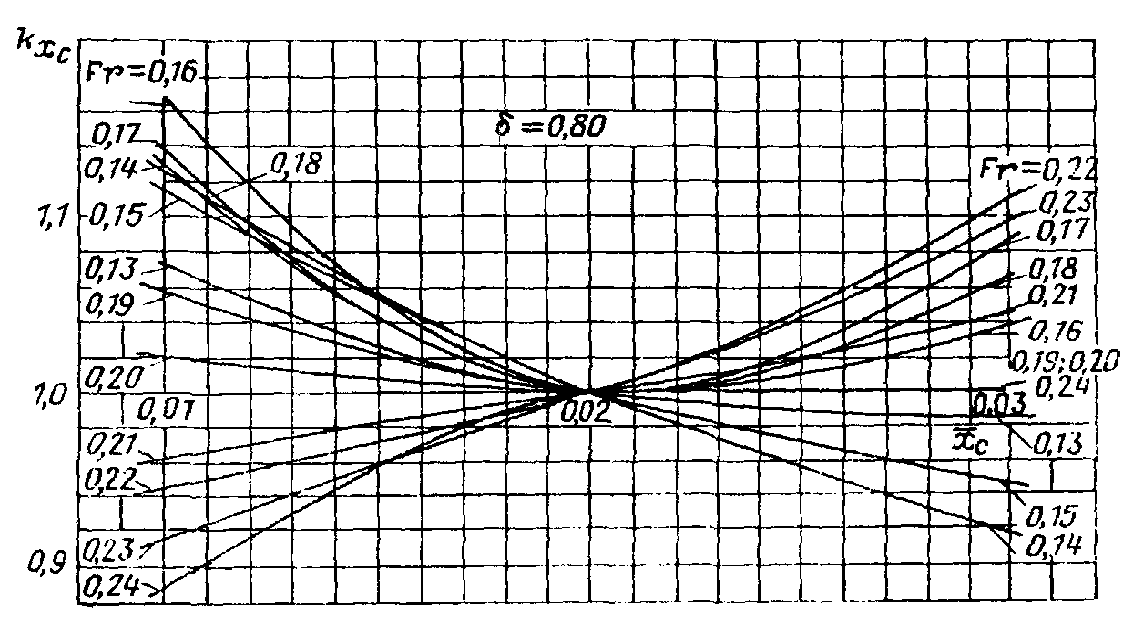
Рис. П.15. Зависимость
коэффициента влияния
 от
.
от
.
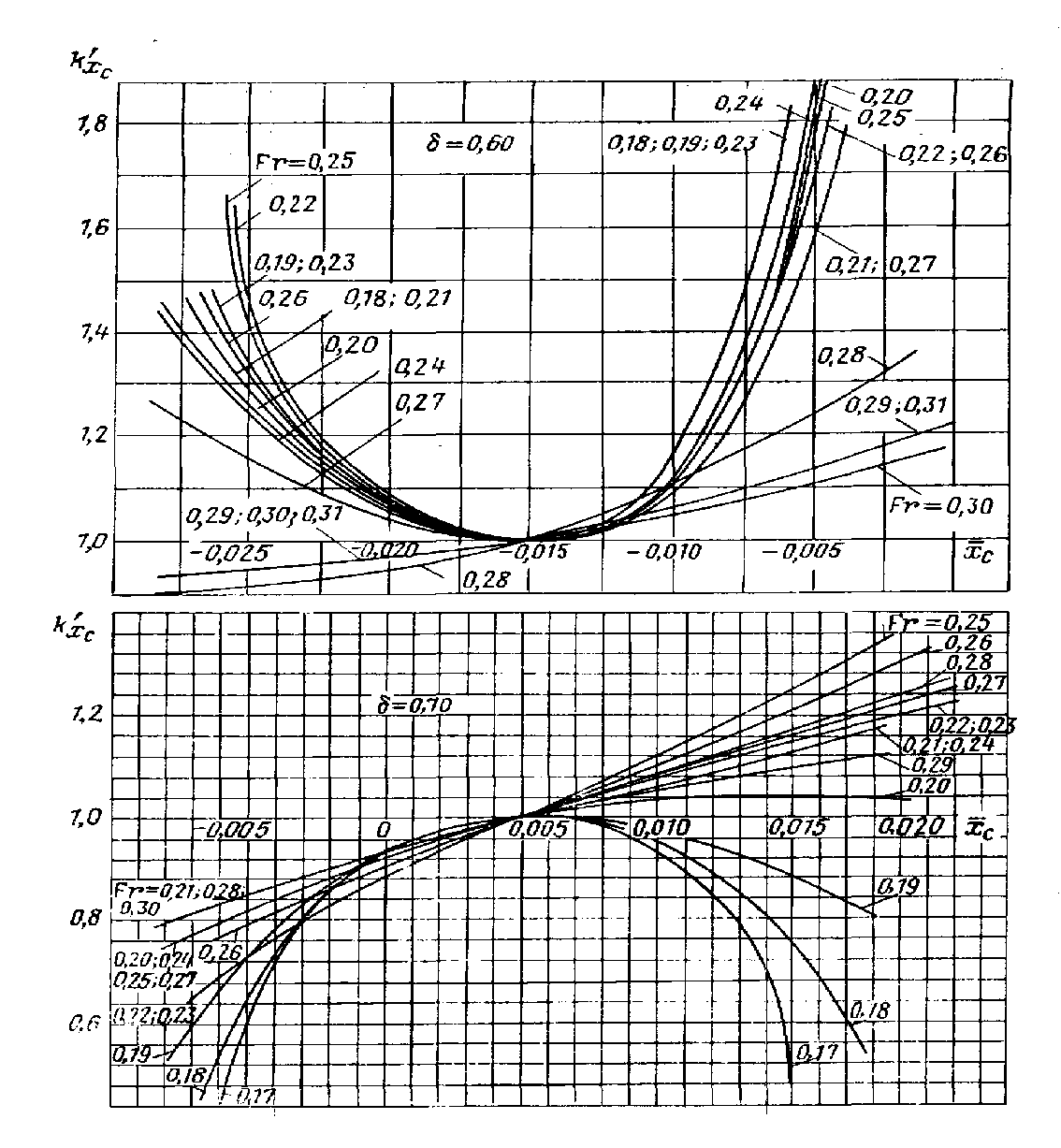
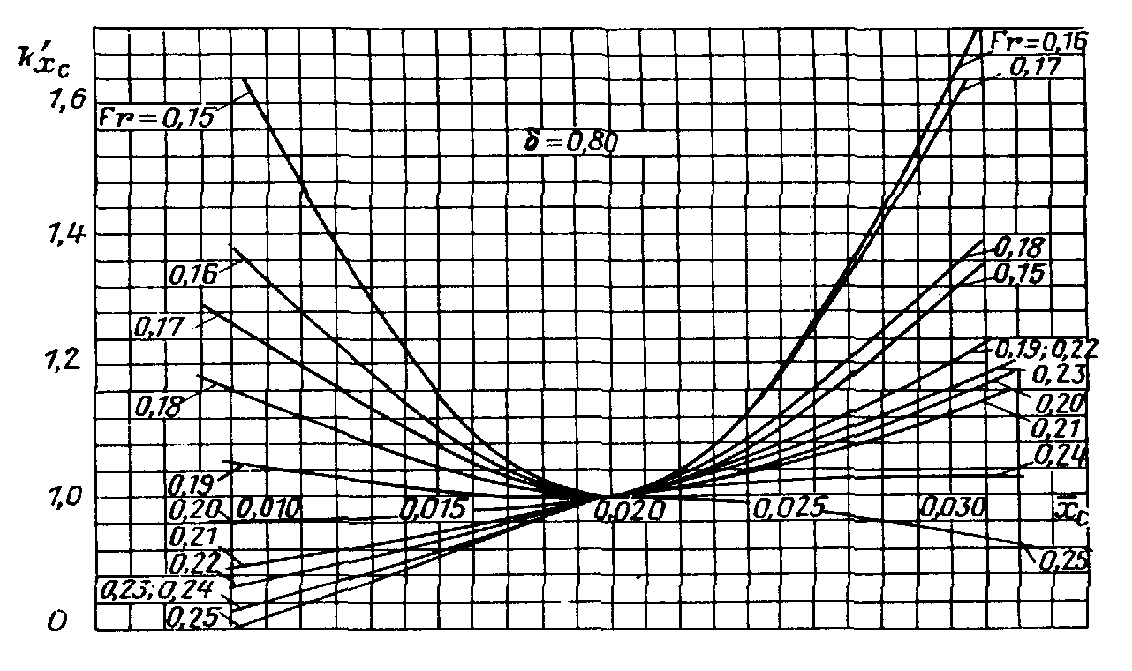
Рис.
П.16. Зависимость коэффициента
 от
.
от
.
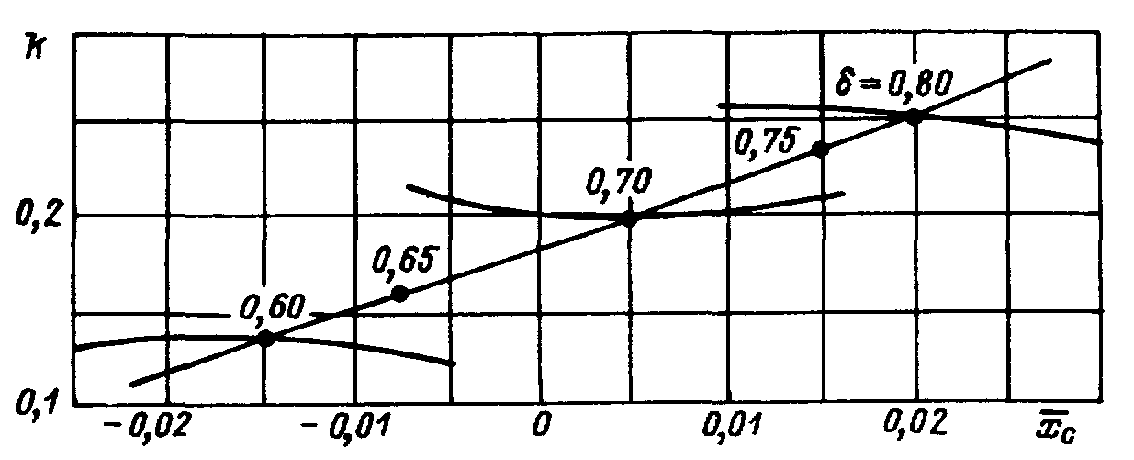
Рис. П.17. Зависимость форм-фактора k от и .
Таблица П.2. Расчет буксировочной мощности по материалам серии судов с умеренной полнотой обводов
-
№
п/п.
Обозначение расчетных величин
Численные значения
1
12
13
14
15
16
17
2
6,18
6,70
7,20
7,72
8,24
8,75
3
38,19
44,89
51,84
59,60
67,90
76,56
4
0,144
0,156
0,168
0,180
0,193
0,204
5
, (см. Рис. П.12)
0,760
0,780
0,840
0,840
0,980
1,100
6
(см. Рис. П.15)
1,000
1,010
1,010
1,040
1,065
1,080
7
(см. Рис. П.13)
0,78
0,78
0,78
0,78
0,78
0,78
8
 (см. Рис. П.14)
(см. Рис. П.14)1,042
1,042
1,042
1,042
1,042
1,042
9
0,618
0,640
0,689
0,794
0,848
0,965
10
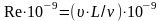
7,15
7,76
8,34
8,94
9,55
10,15
11
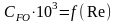 [по формуле (II.4)]
[по формуле (II.4)]1,638
1,621
1,606
1,592
1,579
1,568
12
0,20
0,20
0,20
0,20
0,20
0,20
13
0,10
0,10
0,10
0,10
0,10
0,10
14

2,556
2,561
2,595
2,686
2,727
2,833
15
 ,
кН
,
кН289,4
340,9
398,9
474,7
549,1
643,2
16
 ,
кВт
,
кВт1790
2280
2870
3660
4520
5630

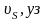


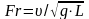
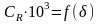 ,
(см. Рис. П.2)
,
(см. Рис. П.2)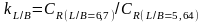 (см. Рис. IV.4)
(см. Рис. IV.4)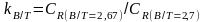 (см. Рис. П.16)
(см. Рис. П.16)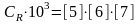

 [по формуле (II.4)]
[по формуле (II.4)]


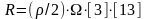 ,
кН
,
кН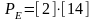 ,
кВт
,
кВт