Лекции / Т4_ДГМ

на него. Поэтому при синтезе наблюдающего устройства потребуется оценивать не только переменные & , но и возмущающее воздействие ur . Нетрудно показать, что попытка избавиться от цветного шума наблюдения за счет дальнейшего повышения порядка объекта не может привести к положительным результатам. Во-первых в этом случае придется оценивать и координаты формирующего фильтра uK , что вряд ли целесообразно. Вовторых, задача становиться некорректной относительно выбора матрицы коэффициентов наблюдающего устройства, поскольку в этом случае шум наблюдений будет рассматриваться как шум, возбуждающий состояние объекта, а измерительный канал оказывается вообще не зашумленным. Следовательно, можно заранее утверждать что значения коэффициентов наблюдателя необходимо выбирать бесконечно большими. Поэтому дальнейшее преобразование объекта с целью приведения его математического описания к ранее рассмотренной задаче необходимо выполнять другим путем. Этого можно добиться, если в качестве измеряемой переменной выбрать фиктивную переменную

В результате такого выбора измеряемых переменных измеряемые фиктивные переменные возбуждаются случайными процессами типа «белого шума». Таким образом, выполнение преобразования привели математическое описание объекта к виду:

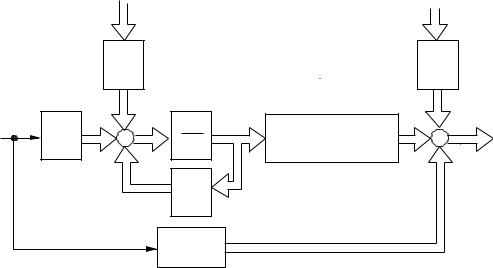
когда сам объект и его измеряемые переменные возбуждаются случайными процессами типа «белого шума». Соответствующая (4-21) структурная схема показана на рисунке 4.8.

54

Рисунок 4.8

При таком описании объекта оценка расширенного вектора состояния может быть выполнена с помощью наблюдающего устройства, построенного в соответствии с уравнением:

представляет оценку этого вектора.

Следовательно, для определения матрицы оптимальных коэффициентов наблюдающего устройства ] можно воспользоваться уравнениями, аналогичными (4-13), (4-14), которые для рассматриваемого случая будут иметь вид:

55

] / Z KZ , •Kt •K, + ,

где / - решение матричного уравнения Риккати следующего вида:

0 / / , •t •, /…Z KZ†,…•Kt •K,†+ …Z KZ†/.

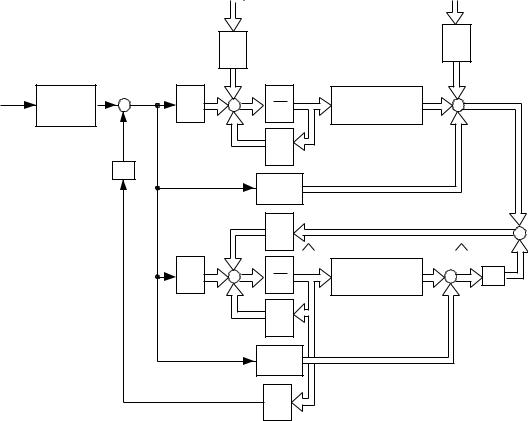
Структурная схема расширенного объекта совместно с наблюдающим устройством представлена на рисунке 4.9.

ωµ

Рисунок 4.9

Необходимо отметить, что с целью устранения операции дифференцирования измеряемых переменных, структурную схему наблюдающего устройства целесообразно преобразовать к виду рисунок 4.10.

56

y(p)

Рисунок 4.10

Важным этапом проектирования оптимальных систем управления со случайными воздействиями является оценка их технических характеристик. За меру качества стабилизации управляемой переменной на заданном уровне при действии на систему случайного процесса q qr qK , обычно принимают значение дисперсии или корень квадратный из неё, то есть так называемый «стандарт». В практических приложениях часто бывает необходимо знать значение дисперсии не только для управляемой, но и для других переменных состояния системы.

С целью расчёта величин дисперсий переменных состояния, при действии на объект случайных воздействий, структурную схему системы целесообразно представить в виде, приведённым на рисунке 4.11.

На основании этой схемы векторно-матричное описание системы, замкнутой через наблюдающее устройство, может быть представлено как:

где отдельные матрицы определены следующим образом

57

з/ /,з tз 0,

известное как векторно-матричное уравнение Ляпунова. В этом уравнении матрица / имеет размерность 4n×4n при условии, что все переменные состояния возмущаются. Если представить матрицу / в блочном виде

58

интенсивностью и как возмущаются переменные состояния расширенного объекта и зашумляются измеряемые переменные.

Рисунок 4.12

На выходную переменную объекта случайным образом действует момент статических сопротивления xŠE . Его изменение соответствует

59

Такой процесс может быть получен на выходе линейной системы первого порядка, возбуждаемой «белым» шумом qŠr с уровнем интенсивности Œr€, которая описывается как

Доступной измерению является всего одна переменная объекта управления, которой является скорость вращения исполнительного двигателя. На её измерения аддитивно наложена случайная помеха, сигнал которой может быть сформирован на выходе линейной системы, возбуждаемой «белым» шумом» qŠK с интенсивностью ŒK€

Для заданного объекта требуется разработать систему управления,

оптимальную с точки зрения минимизации критерия

= Vvwxy ?; .

Следовательно, необходимо спроектировать оптимальное наблюдающее устройство и оптимальный регулятор.

Поставленная задача может быть условно разделена на две части: определение структуры оптимальной системы, включающей в себя

наблюдающее устройство и регулятор; расчет значений коэффициентов 60

наблюдающего устройства ] и коэффициентов оптимального регулятора *. Чтобы правильно составить структурную схему наблюдателя, при такой постановке задачи, необходимо пользоваться математическим описанием расширенного объекта, а в качестве доступной измерению использовать фиктивную переменную "{", определяемую как

{„ K„

Вэтом случае уравнение наблюдателя имеет вид:

С учётом полученного результата по формированию фиктивной переменной {‡ структурная схема оптимальной системы, включающей в

61

себя наблюдающее устройство и регулятор, приведена на рисунке.4.13. Как следует из этой схемы, чтобы исключить операцию дифференцирования, при

формировании { , сигнал разности между { и {‡ вводится через соответствующие коэффициенты ] как на вход интегрирующих звеньев, входящих в состав математического описания объекта, так и на их выход.

62

Рисунок 4.13

63