
Лекции / Т4_ДГМ
.pdfТЕМА 4. ПРОЕКТИРОВАНИЕ ЛИНЕЙНЫХ ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
4.1 Проектирование линейных оптимальных детерминированных
систем управления.
Рассмотрим постановку и решение задачи построения линейного оптимального регулятора/ Пусть объект управления описывается
матричными уравнениями: |
|
|
|
|
|
|
|
|
|
||
|
|
, |
|
|
|
||||||
|
|
|
|
|
(4-1) |
||||||
|
|
|
|
|
|
|
|
|
|
||
где мерный вектор |
состояния |
системы; скалярное управление; |
|||||||||
|
матрица |
объекта; |
1 |
) |
вектор |
входа. Матрица |
|||||
размером 1 устанавливает связь между вектором |
и управляемой |
||||||||||
переменной . |
|
|
|
|
|
|
|
|
|
|
|
За критерий качества работы принимается значение интеграла от |
|||||||||||
квадратичной формы: |
|
! , |
|
|
|
|
|||||
|
""$# |
|
|
|
(4-2) |
||||||
где и положительные весовые коэффициенты. |
& ' ' , при |
||||||||||
Требуется определить такое управление , |
|||||||||||
котором перевод объекта (4-1) из некоторого начального состояния & |
|||||||||||
& в нулевое обеспечит минимум квадратичному интегральному критерию |
|||||||||||
качества (4-2). |
|
|
|
|
|
|
|
|
|
|
|
Поставленная задача относится к классу вариационных и |
|||||||||||
сводится к решению дифференциального уравнения Риккати: |
|||||||||||
|
|
|
|
|
|
|
|
|
(4-3) |
||
|
-P t =DTρ1D-P t |
Bρ2-1BTP t +P t |
A+ATP t |
||||||||
c конечным условием ( |
0. |
|
|
|
|
|
|
|
|||
Зная решение ( |
можно определить матрицу коэффициентов |
||||||||||
обратных связей * размером |
1 в соответствии с выражением |
||||||||||
|
|
* + ,( |
|
|
(4-4) |
34 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
исформировать оптимальное управление в виде линейного закона.
Кпрактическим трудностям реализации оптимального закона (4-
4)следует отнести не только необходимость измерения всех переменных вектора состояния , но и изменение коэффициентов обратных связей во времени. Кроме этого, выбор параметров весовых коэффициентов и в критерии (4-2) является самостоятельной задачей, требующей в каждом
конкретном случае индивидуального решения.
Для многих систем управления электромеханическими объектами представляется целесообразным минимизировать критерий качества (4-2) на
длительных временных интервалах. К таким системам могут быть отнесены следящие системы, системы стабилизации и некоторые другие. При - ∞ рассматриваемая задача синтеза оптимального регулятора несколько
упрощается, поскольку решение уравнения (4-3), если оно существует, стремиться к установившемуся значению (, которое является единственным
неотрицательным симметричным решением алгебраического уравнения
Реккати: 0 , ( + ,( |
( ,( , |
(4-5) |
|
а установившийся закон управления формируется как |
|
||
* , |
(4-6) |
|
|
где матрица коэффициентов регулятора |
|
|
|
* + |
,( |
(4-7) |
|
Достаточно жёсткое |
условие |
существования установившегося |
|
решения (4-5), а следовательно, и возможности построения оптимальной системы, основано на проверке свойства управляемости объекта управления. Объект обладает полной управляемостью лишь в том случае, когда ранг
матрицы управляемости
/у & 1 1 1 2 1 3+
равен порядку объекта, то есть 45 6/у . Ранг матрицы равен наивысшему порядку отличных от нуля миноров этой матрицы.
35
4.1.1. Пример проектирования линейной оптимальной системы.
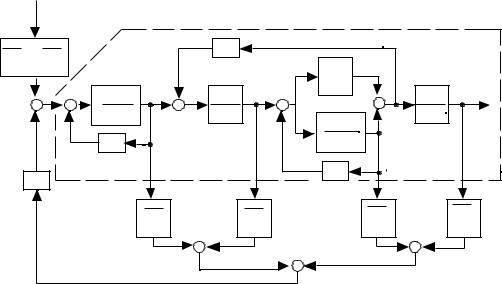
Пусть математическое описание объекта управления задано в виде структурной схемы, очерченной на рис.4.1 пунктирной линией.
uy(p)
k2+ k4 |
|
-1 |
|
|
|
|
|
x1 |
1 |
x2 |
|
1 |
x4 |
||
1 |
|
||||||
|
|
|
kc12 |
|
|
|
|
T эp |
|
Tм1p |
1 |
x |
Tм2p |
|
|
-1 |
|
|
|
|
|
||
|
объект |
Tc12p |
3 |
|
|
|
|
|
|
-1 |
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
k |
k3 |
|
k |
4 |
|
1 |
|
2 |
|
|
|
|
Рисунок 4.1 Требуется определить матрицу строку коэффициентов обратных связей
* 789 89 89: 89;<, замыкание объекта через которую, при переводе системы из некоторого не нулевого состояния в нулевое, обеспечит минимум
интегральному квадратичному" |
критерию качества |
|
|
|
|
||||||
= > ?; |
! |
|
|
|
|
||||||
|
& |
|
|
|
|
|
|
|
|
|
|
В критерий качества входят два неопределённых весовых |
|||||||||||
коэффициента и , поэтому |
для |
нахождения |
конкретного |
решения |
|||||||
целесообразно приравнять |
1 |
и определять коэффициенты оптимального |
|||||||||
регулятора для различных значений , изменяя их в широких 1 |
пределах, |
||||||||||
например: = 0,1; 0,05; 0,01; |
0,001; 0,0005. |
|
|
|
|
|
|||||
Пусть параметры |
|
объекта |
характеризуются следующими |
||||||||
|
@ |
|
0,313 C. , @ |
5,72 C. , @ 0,0049. , 8 |
E |
|
|||||
числовыми значениями: |
|
A |
|
|
E |
A |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
36 |
0,017, @Kэ 0,01 c.
Чтобы использовать специальные программные средства для расчёта коэффициентов оптимальных регуляторов, необходимо описание объекта представить в векторно-матричной форме записи. С учётом принятых на структурной схеме объекта обозначений для переменных вектора состояния, такое описание может быть представлено как
|
P |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
||
|
|
|
|
0 |
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|||||||||
|
TμЭ |
|
|
|
|
|
|
|
|
T |
||||||||||||||||||
|
O |
|
1 |
|
kc12 |
|
1 |
|
|
|
|
|
kc12 |
R |
|
|
1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
O |
|
- |
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
R |
|
P |
TμЭ |
S |
|
|||
|
Tм1 |
Tм1 |
Tм |
|
|
Tм1 |
; |
|
||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|||||||||||||||||||||
|
= O |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
R |
B= |
|
; |
|||
O |
0 |
|
1 |
|
|
|
|
0 |
|
- |
|
1 |
|
|
R |
|
O |
0 |
R |
|||||||||
|
|
Tc12 |
|
|
|
|
Tc12 |
|
||||||||||||||||||||
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
0 |
|
||||||||||
|
O |
0 |
|
|
|
kc12 |
|
|
|
|
|
1 |
- |
kc12 |
R |
|
N |
|
Q |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
O |
|
|
|
|
|
|
Tм2 |
|
|
|
Tм2 |
|
|
|
Tм2 |
R |
|
|
|
|
|
||||||
0 0 0N1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
||||
Для расчета коэффициентов * могут быть использованы
инструментальные средства из состава Matlab. С этой целью в командном |
||||
окне Matlab необходимо предварительно определить |
матрицы |
, , /, U, |
||
после чего издать команду |
* VW4 , , , U . |
|
|
1 , |
Матрицу / , для нашего примера, |
так |
как |
||
следует определить как квадратную матрицу размером 4 4, |
единственным |
|||
элементом в которой является W;; 1. Скаляр U задаёт весовой коэффициент
, с которым управляющее воздействие входит в интегральный критерий
качества. Результаты применения указанных специальных средств представлены в следующей таблице 4.1. На завершающем этапе проектирования необходимо определить, анализируя весь перечень требований предъявляемых к системе, какую из пяти вариантов оптимальных систем возможно практически применить. Например, если ограничить по техническим соображениям допустимую величину управляющего воздействия для чего установить на входе объекта управления нелинейное
37
|
|
Таблица 4.1 |
|
|
|
1 |
|
|
|
|
0,1 |
0,05 |
0,01 |
0,001 |
0,0005 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
0,1058 |
0,1266 |
0,1825 |
0,2875 |
0,3268 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
3,481 |
4,206 |
6,224 |
10,28 |
11,88 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
: |
|
100,1 |
143,2 |
298,0 |
740,1 |
956,3 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
; |
|
0,3192 |
0,2664 |
3,776 |
21,35 |
32,84 |
|
|
|
|||||
|
|
|
|
|
|
|
|
звено типа «ограничение». В этом случае в системе с регуляторами, рассчитанными для значений '0,001, возникают автоколебания. Желая исключить это явление, целесообразно выбрать коэффициенты регулятора, рассчитанные для значений 0,01.
4.2 Наблюдающие устройства идентификации полного порядка
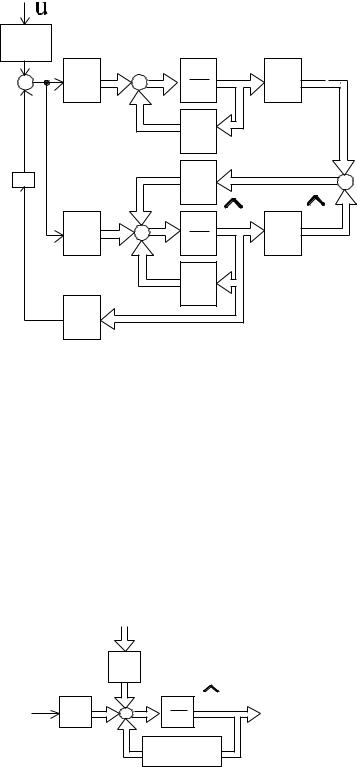
Если на основе информации о переменных состояния объекта, полученной от физических датчиков, не удаётся обеспечить требуемое качество управления, необходимо объём информации о векторе состояния объекта увеличить. Этого можно достичь, например, с помощью наблюдающих устройств идентификации полного порядка (наблюдателей). Структурная схема линейной системы оптимального управления, включающая в себя наблюдатель, показана на рисунке 4.2.
Из структурной схемы следует, что если объект управления
представлен как |
|
|
|
|
|
|
|
|
|
, |
|
||||
|
|
|
|
|
|||
где |
|
Y Z |
|
|
вектор входа; |
||
матрица объекта; |
1 ) |
||||||
скалярное управление. |
Матрица |
С размером 4 |
устанавливает связь |
||||
между вектором и измеряемыми переменными Y. |
|
||||||
38
|
у |
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
Wз(0) |
|
|
1 |
x |
|
y |
|
|
B |
|
C |
|||
|
|
|
p |
|
|
||
|
|
|
|
A |
|
|
|
|
-1 |
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
1 |
x |
-C |
y |
|
|
|
p |
|
|
||
|
|
|
|
A |
|
|
|
|
|
K |
|
|
|
|
|
|
|
Рисунок 4.2 |
|
|
|
|
|
В этом случае наблюдающее устройство полного порядка выполняется |
|||||||
в соответствии с уравнением: |
|
|
\ |
|
|
|
|
|
\ |
|
|
|
|
|
|
|
]7Y Z <, |
|
(4-8) |
||||
\ |
|
|
|
|
|
|
|
где ] 4 матрица коэффициентов наблюдателя. |
|
|
|||||
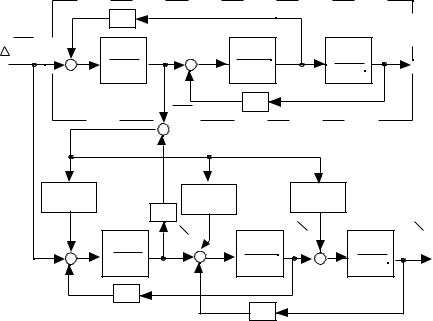
После несложных преобразований структурную схему |
|||||||
наблюдателя можно представить в виде рисунка 4.3. |
|
|
|||||
|
|
|
y(p) |
|
|
|
|
|
|
|
L |
|
|
|
|
|
uу (p) |
B |
1 |
x (p) |
|
|
|
|
|
p |
|
|
|
||
|
|
|
A -LC |
|
|
|
|
|
|
|
Рисунок 4.3 |
|
|
|
|
На основании этой схемы динамические свойства наблюдателя |
|||||||
определяются видом характеристического уравнения |
|
|
|||||
|
det ab ]Z 0 |
|
|
|
|||
|
|
|
|
|
|
|
39 |
4.2.1 Пример проектирования наблюдающего устройства полного
порядка.
Требуется спроектировать наблюдающее устройство полного порядка для объекта, математическое описание которого задано структурной схемой, очерченной пунктирной линией на рисунке 4.4.
|
-1 |
|
|
|
|
x3 |
M(p) |
1 |
x1 |
1 |
x2 |
1 |
|
|
Tм1p |
|
Tcp |
Tм2p |
|
|
|
объект |
ωд |
-1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Tм1l11 |
T |
l21 |
Tм2l31 |
|
|
|
|
-1 |
c |
|
x2 |
|
x3 |
1 |
x1 |
|
1 |
1 |
||
Tм1p |
|
|
Tcp |
|
Tм2p |
|
-1 |
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
Рисунок 4.4 Известно, что доступной измерению является одна переменная-
скорость вращения двигателя ? .
Разработка наблюдающего устройства требует решения двух задач: определения структуры наблюдающего устройства и расчёта матрицы коэффициентов ].
Если структурное построение наблюдающего устройства, при использовании одной измеряемой переменной, достаточно очевидно (рисунок 4.4), то определение коэффициентов ] может быть выполнено на основании различных подходов. Один из таких подходов, широко распространённый на практике, основан на стремлении разместить корни
40

характеристического уравнения наблюдающего устройства в наперёд заданное положение на комплексной плоскости « a ». В данном примере
используем именно этот подход, следовательно, путём выбора |
|||||||||
коэффициентов ] необходимо обеспечить тождество: |
|
|
|||||||
|
det ab |
]Z |
c a , |
|
|
||||
где c a - наперёд заданная стандартная форма. |
|
|
|
|
|||||
Для конкретного примера, с учётом введённых обозначений |
|||||||||
переменных состояния на рис.4.4, определим матрицы |
, ], Z: |
||||||||
|
|
P |
0 |
e# |
0 |
S |
|
|
|
|
|
|
, |
|
|
|
|
||
|
|
|
0 |
|
; |
|
|
||
|
|
,f |
|
,f |
|
|
|
||
|
|
N |
0 |
eg |
0 |
Q |
|
|
|
|
|
|
, |
|
|
|
|
||
] |
V V V: ,; |
|
|
0 0 |
. |
||||
|
|
|
|
С 1 |
|
||||
|
|
Следовательно, |
@A1 |
|
|
|
|
|
|||
|
|
|
P |
a |
|
|
0 S |
V |
0 |
0 |
|
ab ]Z |
1 |
|
a |
1 |
hV |
0 |
0i |
||||
|
|
|
N |
@E |
@A1 |
@E |
V: |
0 |
0 |
||
|
|
|
0 |
a Q |
|
|
|
||||
Таким образом, |
|
det ab ]Z |
|||||||||
a |
|
V a |
|
j@E@A |
|||||||
: |
|
@E@A @Ak a |
|
@E@A |
|||||||
|
|
1 |
|
1 |
|
V |
|
V |
|||
P a |
V |
|
@A1 |
0 S |
|
V |
1 |
|
a |
1 |
|
@E |
|
@E |
|||
N |
V: |
|
@A1 |
a Q |
|
V: |
0 |
l |
@E@A |
Будем стремиться так распределить корни характеристического уравнения наблюдающего устройства на комплексной плоскости «a», чтобы их распределение соответствовало стандартной форме Баттерворта третьего
порядка:
41

c a a: |
2m&нa |
2m&нa+m&н: |
(**) |
|||
Для этого необходимо обеспечить равенство коэффициентов при |
||||||
одинаковых степенях оператора «a» левых частей уравнений (*), (**), т.е.: |
||||||
1 |
V |
2m&н; |
|
|
||
1 |
|
|
V |
|
||
j@E@A |
@E@A k |
@A 2m&н; |
|
|||
2m&н |
V: |
m&н |
|
|
||
@E@A |
@E@A |
V и V: |
|
|||
Откуда следует, |
что коэффициенты |
наблюдающего |
||||
устройства следует определить как: |
|
|
1 |
|
|
|
|
1 |
|
|
|
||
V @A oj@E@A |
@E@A k 2m&н ; |
|
||||
|
: |
|
2m&н |
|
|
|
V: om&н |
@E@A @E@A . |
|
||||
4.2.2Наблюдающие устройства не полного порядка
(редуцированные наблюдатели)
До сох пор мы рассматривали наблюдающие устройства полного порядка. Однако, в ряде случаев это вряд ли целесообразно. На практике измеряемые переменные можно использовать непосредственно для управления, а с помощью наблюдателя восстанавливать только не измеряемую часть переменных состояния объекта.
При построении наблюдающих устройств этого типа весь вектор состояния X разделяют на две части
X = Y ,
W
где Y – вектор измеряемых переменных размером ( r ×1), а W-вектор неизмеряемых переменных размером (n-r) ×1.
В соответствии с принятым разделением вектора X математическое описание объекта может быть представлено в следующем виде:
42
|
• |
|
Y(t) |
||
|
• |
|
W(t)
A11 |
A12 |
Y(t) |
B1 |
|
u(t) |
||
= |
|
|
|
|
+ |
|
|
A21 |
A22 |
W(t) |
B2 |
|
|
||
или в виде двух векторно-матричных уравнений
• |
|
|
|
Y(t) = A11Y(t) + A12W(t) + B1u(t) |
|
(4-9) |
|
• |
|
|
|
|
|
|
|
|
|
|
|
W(t) = A21Y(t) + A22W(t) + B2u(t) |
|
||
Специфика построения |
редуцированных наблюдателей определяется |
||
тем, что необходимо образовывать невязки между не измеряемой частью переменных состояния объекта и её оценками. Для косвенного определения информации о не измеряемой части объекта через измеряемые переменные из первого уравнения (4-9) определяют:
•
A12W(t) = Y(t) − A11Y(t) − B1u(t)
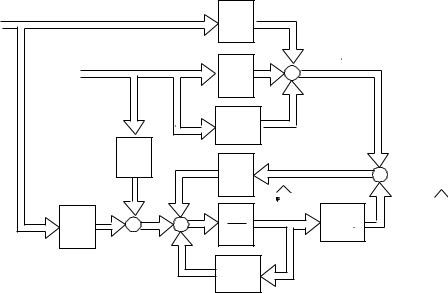
На основании этой информации редуцированное наблюдающее устройство выполняется в соответствии со следующей структурной схемой
u(p) |
|
- B |
|
|
|
|
|
|
|
|
|
|
y |
1 |
|
A12W |
|
|
|
|
|
||
|
(p) |
p |
|
|
|
|
|
|
|
|
|
|
|
-A11 |
|
|
|
|
A21 |
L |
|
|
|
|
|
|
|
|
|
|
|
1 |
W |
|
-A |
B2 |
|
|
-A12 |
12W |
|
|
p |
|
|
||
|
|
A22 |
|
|
|
На основании данной структурной схемы уравнение редуцированного наблюдателя может быть представлено как:
43
