
мой курсаччч
.pdf
МИНОБРНАУКИ РОССИИ
Государственное образовательное учреждение высшего профессионального образования
«Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И.Ульянова (Ленина)»
(СПбГЭТУ)
Факультет ФРТ Кафедра ТОР
КУРСОВАЯ РАБОТА (ПРОЕКТ)
По дисциплине: |
Радиотехнические цепи и сигналы |
На тему: |
Оптимальная фильтрация сигналов |
Выполнил |
Оценка __________________ |
студент гр. 9104 |
Проверил |
Куров А.Г. |
Ушаков В.Н. |
Дата ____________________
Санкт-Петербург 2012г.
Оглавление:
1.Постановка задачи.
2.Задание.
3.Расчёт спектральных характеристик сигнала.
4.Разработка структурной схемы СФ.
5.Расчёт Преобразования сигнала и шума согласованным фильтром.
6.Расчёт квазиоптимального (RC) фильтра.
1. Постановка задачи.
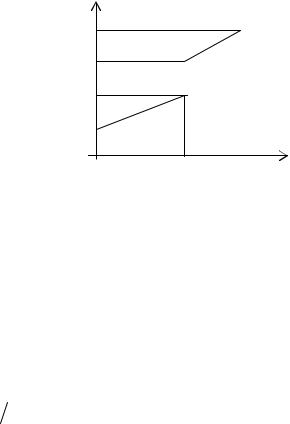
1. В качестве входного сигнала в курсовой работе рассматривается видеоимпульс u(t) ,
заданный на интервале [0,T2 ] двумя отрезками прямых, как показано на рисунке. В каждом индивидуальном задании заданы три
значения параметра T1 . После анализа амплитудных |
u(t) |
|
|
|
|
|
||||||
|
|
|
|
|
|
|||||||
спектров |
сигнала с различными T1 по заданному |
U4 |
|
|
|
|
|
|||||
|
|
|
|
|
||||||||
критерию выбирается одно из значений. |
|
U3 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||||
2. В качестве шумового сигнала в курсовой |
|
|
|
|
|
|
||||||
работе |
рассматривается стационарный |
случайный |
U2 |
|
|
|
|
|
||||
|
|
|
|
|
||||||||
процесс |
в виде квазибелого шума, |
спектральная |
U1 |
|
|
|
|
|
||||
плотность средней мощности W0 которого ограничена |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||
частотой |
fш.гр, |
|
ω |
|
≤ 2πfш.гр. |
|
0 |
Т1 |
Т2 |
t |
||
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||
3. Задание на курсовую работу заключается в следующем:
а) рассчитав амплитудные спектральные функции для трех вариантов заданного входного сигнала, выбрать по указанному далее критерию один из них и, рассчитав для выбранного сигнала комплексную спектральную функцию, ее вещественную и мнимую части, а также фазовый спектр, определить комплексный коэффициент передачи согласованного с ним фильтра (СФ);
б) синтезировать структурную схему СФ и рассчитать форму напряжений в различных ее точках при подаче на вход фильтра импульса напряжения, имеющего вид дельта-функции δ(t) ;
в) рассчитать форму выходного напряжения при воздействии на вход СФ выбранного сигнала, а также видеоимпульса одной (по указанию преподавателя) из следующих форм:
- прямоугольного видеоимпульса, удельная энергия которого равна удельной энергии
выбранного входного сигнала, а длительность Т = 1 f0,1 , где f0,1— частота, на которой уровень
амплитудного спектра |
& |
выбранного входного видеосигнала снижается до уровня |
||||
S (ω) |
||||||
|
(ω) |
|
= 0,1S(0); |
|||
0,1 |
& |
|
||||
S |
|
|||||
|
|
|
|
max |
||
|
|
|
|
|||
|
|
- сигнала, совпадающего по форме с импульсной реакцией СФ (удельная энергия этого |
||||
сигнала также выбирается равной удельной энергии выбранного входного сигнала); |
||||||
г) рассчитать спектр мощности шума на выходе СФ; д) проанализировать эффективность действия СФ, рассчитав выигрыш в отношении с/ш,
обеспечиваемый им для сигналов, рассмотренных в п. 3в; е) исследовать прохождение выбранного сигнала и шума через квазиоптимальный фильтр
ввиде RC-фильтра нижних частот, а именно:
-найти значение постоянной времени RC-фильтра τopt , при котором отношение с/ш на
его выходе максимально (оптимальное значение);
- рассчитать форму напряжения на выходе квазиоптимального фильтра с τopt при
воздействии на его вход выбранного сигнала;
-определить выигрыш в отношении с/ш, который дает квазиоптимальный фильтр, и сравнить его со значением, полученным для согласованного фильтра;
-рассчитать амплитудно-частотную и фазочастотную характеристики (АЧХ и ФЧХ)
квазиоптимального фильтра с τopt , а также спектр мощности шума на его выходе.
2. Задание.
2.1 Таблица с параметрами задания.
№ |
U1,В |
U2,В |
U3,В |
U4,В |
T1,мкс |
n |
m |
19 |
2 |
10 |
10 |
0 |
2 |
12 |
40 |
|
|
|
|
|
|
|
|
T2=5 мкс |
|
|
|
|
|
|
|
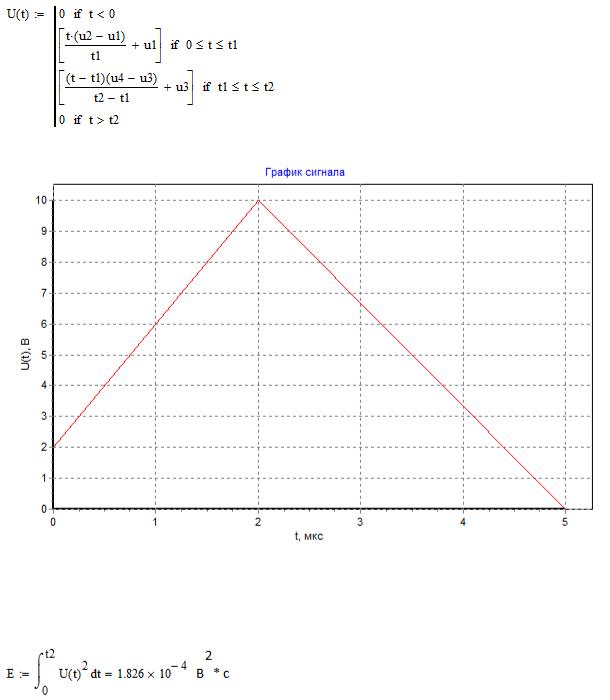
2.2 Представление заданного сигнала u(t) в аналитической форме. Расчёт энергии Е сигнала u(t) и параметров шума fш.гр. и СПМ W0(ω).
Общее аналитическое выражение входного сигнала выглядит следующим образом:
∞
Расчет энергии сигналов: E = ∫u 2 (t)dt
−∞
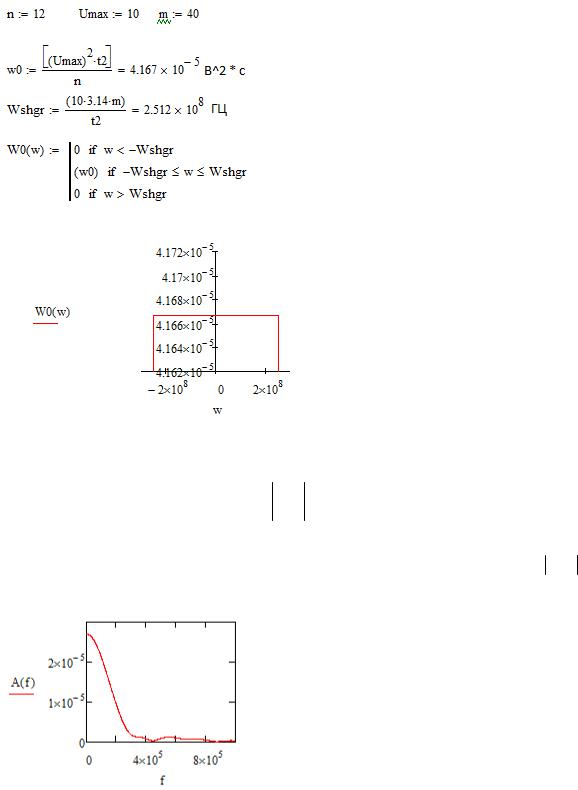
Расчёт параметров шума Wshgr и спектральной плотности мощности W0(ω)
3. Расчёт спектральных характеристик сигнала.
·
3.1 Расчет модуля спектральной функции S (ω ) для трёх вариантов входного сигнала.
¥
Для расчёта АЧХ сигналов воспользуемся формулой: S ( f ) = ∫U (t) ×e- j 2π × f ×t dt , A( f ) = S( f ) .
-¥
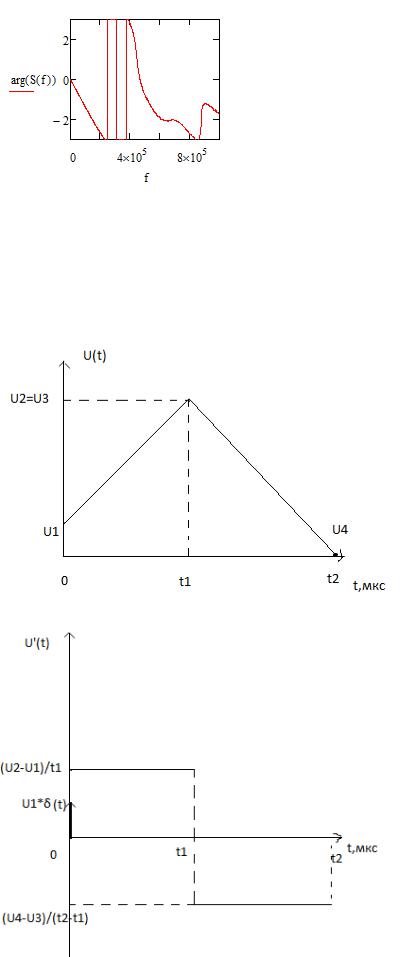
3.2 Расчёт фазового спектра φs(f) для выбранного сигнала.
3.3 Вывод аналитического выражения для спектральной функции выбранного сигнала. Запись
∙ |
∙ |
|
∙ |
спектральной функции в виде: S ( f ) = Re S ( f ) |
+ j Im S ( f ) . |
||
|
|
|
|
Для вывода аналитического выражения спектральной функции сигнала воспользуемся методом
,B
дифференцирования (в данном случае двойного)
,(B/c)
,(B/c)
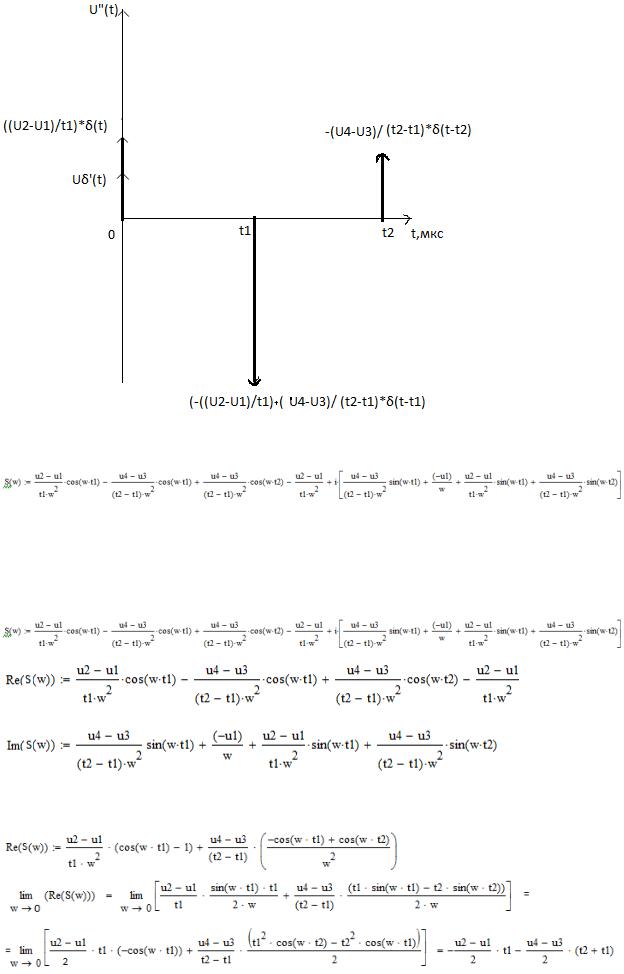
Получим конечное аналитическое выражение для спектра сигнала:
|
|
|
|
|
∙ |
|
3.4 Аналитическое определение пределов lim Re S (ω ) |
и |
|||||
|
|
|
ω →0 |
|
|
|
∙ |
∙ |
|
∙ |
|
|
|
S ( f ) = Re S ( f ) |
+ j Im S ( f ) |
|
|
|
||
|
|
|
|
|
|
|
|
|
∙ |
1) lim Re S (ω ) |
||
ω →0 |
|
|
lim Im
ω→0
∙ (ω ) .
S

|
|
∙ |
2) lim Im S (ω ) |
||
ω→0 |
|
|
3.5 Контрольный ручной расчет |
& |
( f ) |
& |
& |
(ω )) для f1 |
= 10 |
6 |
f2 |
6 |
S |
, Re(S |
(ω )) и Im(S |
|
= 2*10 . |
1) Расчет мнимой части:
f=106 Гц
f=2*106 Гц
2) Расчет действительной части:
f=106 Гц
f=2*106 Гц
3)Расчет &( ) :
S f
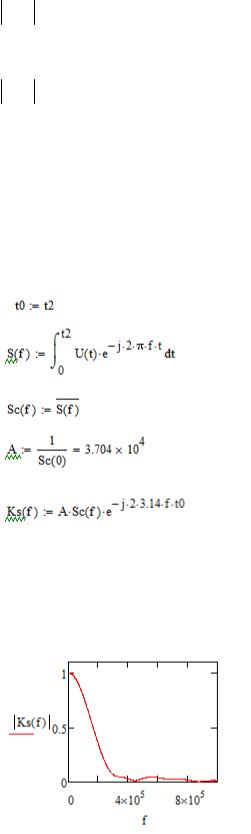
f=106 Гц
&( ) 3.183*10^-7
=
S f
f=2*106 Гц
&( ) 1.592*10^-7
=
f
S
4. Разработка структурной схемы СФ.
4.1 Вывод аналитического выражения для комплексного коэффициента передачи СФ в виде:
& |
|
(ω )×e |
− jωt0 |
. |
KS (ω ) = A× S |
|
|
& |
(0) = 1 находим А: |
Из условия K S |
АЧХ и ФЧХ комплексного коэффициента передачи СФ:
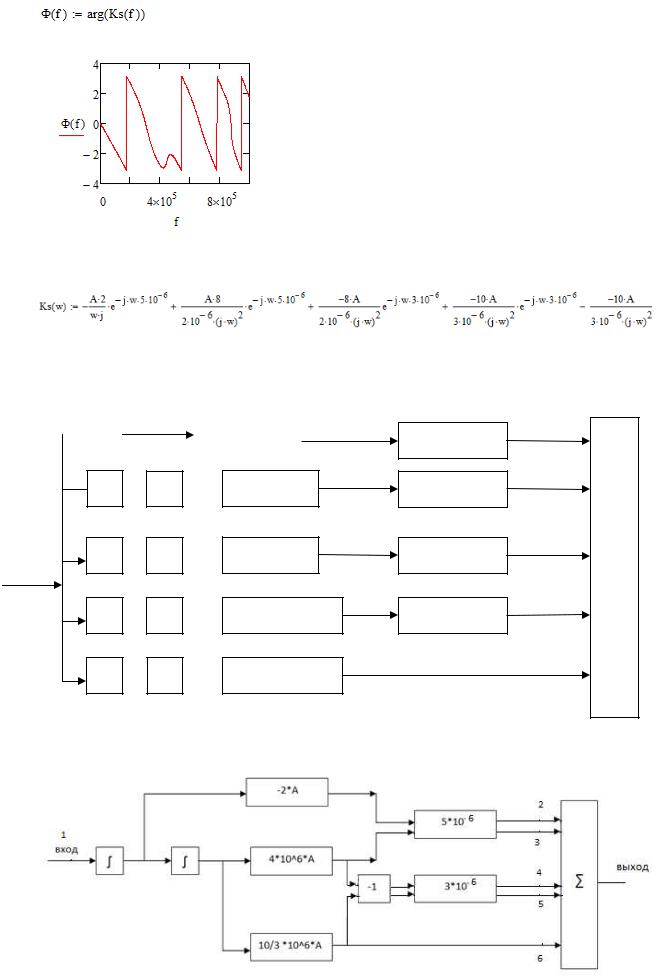
Подставляя значения, получу:
4.2 Синтез и модификация структурной схемы СФ.
|
∫ |
|
-2*A |
|
|
||
|
|
|
|
∫  ∫
∫  4*10^6*A
4*10^6*A
∫ 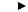 ∫
∫  -4*10^6*A
-4*10^6*A
вход
∫  ∫
∫  -10/3 *10^6*A
-10/3 *10^6*A
∫  ∫
∫  10/3 *10^6*A
10/3 *10^6*A
Упрощенная структурная схема:
5*10-6
5*10-6
3*10-6
∑
3*10-6
7
