Добавил:

posterp Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Днепропетровский национальный университет железнодорожного транспорта им. академика В. Лазаряна

Предмет:

Физика

Файл:

Obr_eksp_rez

.pdf

Скачиваний:

Добавлен:

27.04.2021

Размер:

463.39 Кб

Скачать

☆

<<< < Предыдущая 12 / 32 3 > Следующая >>>

					n					10
σ 2 =					n		s2		;	(10)
				n −1
σcp2		. =		1			s2 .			(11)
					n −1
В якості найкращої оцінки							s2			візьмемо s2 . Тоді для σcp. отримуємо
наближений вираз:					s
σ			≈		s			.		(12)
σ			≈		(n −		1	.		(12)
	cp.				(n −	1)2

Вирази (10) − (12) − це незміщені оцінки величин σ 2 та σcp2 . .

2.3.3. Розподіл Гауса

Оскільки при відсутності систематичних похибок найбільших впливів набувають випадкові похибки, то згідно з центральною граничною теоремою Ляпунова [3 − 12], стверджують, що результати вимірювань та їх похибки повинні мати нормальний закон розподілу (закон Гауса).

Можна показати, що для випадку розподілу Гауса найкращим наближенням величини X буде середнє арифметичне x і навпаки, якщо найкращим наближенням до істинного значення є середнє арифметичне, то

розподіл − гаусівський (нормальний).
Функція f (x) розподілу Гауса задається двома параметрами X і σ :
				x−X	2
			−	x−X
	1
f (x)=
f (x)=		σ	e	2σ2		.	(13)
	2π	σ				f (x) нормального розподілу:
Відмітимо основні особливості функції						f (x) нормального розподілу:

–симетрична відносно X ;

–досягає максимуму в точці X ;

– швидко прямує до нуля при x − X >σ ;

–точки x = ±σ є точками перегину;

–нормована до одиниці: +∞∫ f (x)dx =1.

−∞

Знаючи f (x), можна по (4) порахувати середньоквадратичне відхилення:

+∞	12π	σ1	+∞	−	x2
(сер.кв.відх.)2 = ∫(x − X )2 f (x)dx =			∫x2 e			dx =σ 2 .
					2σ 2
−∞			−∞

Поряд із середньоквадратичним відхиленням часто використовують середнє відхилення (або середню похибку):

+∞

∞

−

r = | ∆| =

x − X f (x)dx =

2σ2 dx =

∫

σ . (14)

2π

−∞

При обрахунках в якості r використовують: r = 1 ∑ di . n i

Враховуючи (14) можна отримати зручну формулу для обчислення σcp. :


σcp.	=	π	r			≈		5		r			;	(15)
σcp.	=	2	(n −	1		≈		4		(n −	1		;	(15)
		2	(n −	1)2				4		(n −	1)2
							5			n	1

	σ =		n σcp.		≈							2	r .	(16)
	σ =		n σcp.		≈		4						r .	(16)
							4		n −1

В літературі формула (15) називається формулою Пітерса. Використовуючи функцію щільності розподілу, введемо функцію

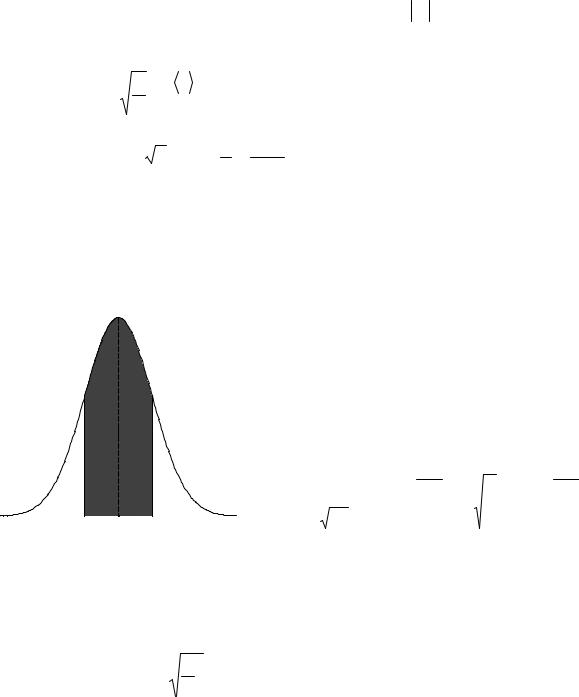
розподілу F(x). Нехай f (x) крива розподілу з X = 0 . Визначимо, яка частка виміряних значень припадає на інтервал від − x до + x , тобто:

f(t)

	-x 0	x	t
Мал. 3.	F(x), частка	виміряних
значень	в інтервалі	±x,	рівна

площі заштрихованої ділянки.

F (x)=	+∫x f (t)dt .		(17)
Функція	−x	F(x)	називається

функцією розподілу. Вона чисельно рівна площі заштрихованої ділянки на мал. 3.

Підставивши в (17)

f (x)

для

розподілу Гауса, маємо:

−

F(x)=

e 2σ2dt =

2σ2dt.

∫

∫e

π σ

−x

π σ

Ввівши нову змiнну τ =

і позначивши

z =

, отримуємо:

F(z)=		2	z −	τ2
				2 dτ .	(18)
		π	∫e
			0
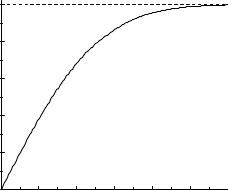
Значення функцій	f (x)		та F(z) приведені в табл. 1 додатку, а на мал. 4
представлено графік	F(z).		Слід	пам'ятати,	що в межах ±σ знаходяться

приблизно дві третини результатів. Це дозволяє контролювати правильність обчислення σ . Поза інтервалом ± 2σ залишається двадцята частина результатів, а поза ±3σ − лише чотирьохсота частина.

Коротко відмітимо основні властивості випадкових похибок.

1,0
F(z)
0,8
0,6
0,4
0,2
0,0	0,5	1,0	1,5	2,0	2,5z=x/σ
0,0	0,5	1,0	1,5	2,0	2,5z=x/σ
Мал. 4. Функція розподілу F(z) для
	розподілу Гауса.

Якщо похибки вимірювань випадкові, вони підлягають нормальному закону розподілу. Вивчаючи розподіл випадкових похибок, було виявлено такі статистичні закономірності, відомі як властивості випадкових похибок:

1.При даних умовах вимірювань випадкові похибки за своєю абсолютною величиною не можуть переходити певну межу. Ця властивість характеризує умови вимірювань, точність приладу, методику, тощо.

2.Малі за абсолютною величиною похибки зустрічаються частіше, ніж великі. Це, по суті, − відображення закону розподілу.

3.Додатні похибки з'являються так само часто, як і рівні їм за абсолютною величиною від'ємні. Ця властивість є наслідком дії закону великих чисел.

4.Середнє арифметичне випадкових похибок однієї і тієї ж величини прямує до нуля при зростанні кількості вимірювань:

lim ∑∆i = 0 .

n→∞ n

5.Випадкові похибки при переході від одного вимірювання до іншого змінюють свою величину та знак без будь-якої закономірності. Ця властивість випливає з властивостей будь-якої випадкової величини, про конкретний результат якої не можна сказати наперед.

Ще раз випишемо основні формули для обчислення σ і σcp. :

∑di2

∑

≈

;

≈

;

n(n

−1)

(n −

cp.

1)2

∑

σ ≈ ∑di2

;

σ ≈

;

= x − x .

n −1

[n(n −1)]

2.3.4. Розподіл похибок заокруглення

При виконанні будь-яких обчислень завжди зустрічаємось з необхідністю заокруглювати результати до певного десяткового знаку, користуючись відомим правилом Гауса. Це правило виключає однобічне

накопичення помилок та дозволяє мати цілком ідентичні результати, коли ті ж самі обчислення виконують різні особи.

Досвідом встановлено такі властивості похибок заокруглення:

1)гранична похибка заокруглення становить 1/2 одиниці останнього отриманого десяткового розряду;

2)додатні та від'ємні похибки заокруглення рівноможливі;

3)математичне сподівання (середнє значення) похибок заокруглення рівне

нулю;

4)великі та малі похибки заокруглення рівноможливі.

Остання властивість суттєво відрізняє похибки заокруглення від випадкових, тому, що вони не мають нормального розподілу. Похибки заокруглення підлягають рівномірному закону розподілу. Середнє значення та дисперсія рівномірно розподіленої випадкової величини дорівнюють:

x = ∫x

f (x)dx =

1 ∫x dx = a + b ;

b − a

σ 2 = ∫b (x − X )2 f

(x)dx =

∫b (x − X )2 dx = (b −a)2 .

b −a

x = a + b ;

σ 2

(b −a)2 ,

(19)

де

a і b − межі розподілу, при a ≤ x ≤ b щільність розподілу постійна:

f (x)=

b −a

Якщо випадкова величина x розподілена рівномірно на інтервалі a0 ±α ,

де a0 − математичне сподівання, то, враховуючи (19), дисперсія буде:

σ 2 = [(a0 +α)−(a0 −α)]2

= α2 ,

(20)

а середньоквадратичне відхилення

σ =

α .

(21)

Якщо прийняти

α за

граничну

похибку

заокруглення, то σ буде

середньоквадратичною похибкою заокруглення.

При проведенні обчислень, наприклад, з точністю до m розрядів після

десяткової коми гранична похибка		α числа становить 0.5 10−m , а
середньоквадратичне значення − σ =	10−m
	2	.
		3

2.4. Обчислення похибок прямих вимірювань

Мета будь-якого фізичного експерименту полягає в тому, щоб, маючи інформацію про природу і величину похибок вимірювань, зробити відповідні висновки про істинне значення вимірюваної величини. Треба врахувати те, що похибки вимірювань бувають різного типу: це здебільшого похибки приладу, похибки заокруглення, систематичні і випадкові похибки. Розглянемо, як враховувати кожну похибку зокрема.

2.4.1. Систематичні похибки

Систематичні похибки, пов'язані з методикою досліду, враховуються так, як вказано в описі роботи. Систематичні похибки, пов'язані з використанням приладів, треба усувати в процесі проведення експерименту. Так, потрібно правильно встановити прилад, перевірити положення нульового відліку шкали. Якщо нуль “збитий”, то слід встановити його або вводити відповідні поправки у виміри.

2.4.2. Випадкові похибки

Випадкові похибки виявляються шляхом багатократних вимірювань, тоді як систематичні похибки не можна виявити шляхом повторних вимірювань тим самим приладом.

Нехай при повторних рівноточних вимірюваннях (що проводяться в одинакових умовах, одним дослідником, одним і тим самим приладом) отримаємо n значень відповідної фізичної величини, які трохи відрізняються одне від одного: x1, x2 ,..., xn .

Відомо, що найбільш ймовірним значенням вимірюваної величини буде

середнє арифметичне значення: x = 1 ∑xi . n i

Точність вимірювань характеризується також відносною похибкою E ,

рівною відношенню абсолютної похибки ∆x до значення x : E = |∆xx| .

Чим менша відносна похибка, тим вища точність вимірювання. Оскільки похибки випадкові, то для характеристики величини похибки

треба вказати два числа: величину самої похибки, тобто надійний інтервал

± ∆x , і рівень вірогідності (ймовірнісна характеристика) P , що показує, яка частка всіх вимірів буде знаходитись у вказаному надійному інтервалі. Якщо одна з цих величин (рівень вірогідності, надійний інтервал) задана, то методами теорії випадкових похибок можна знайти другу. Роглянемо це.

Вибір рівня вірогідності.

Критерії для вибору того чи іншого значення вірогідності визначаються виключно з практичних міркувань. Покажемо це на прикладі.

При виробництві моторів задається певний допуск ∆x для розмірів деталей. Ясно, що авіаційні мотори повинні бути більш надійні, ніж, скажімо, автомобільні. Отже, надійність для цих деталей повинна бути вищою при заданому значенні ∆x , що можна досягти тільки шляхом підвищення точності обробки деталей для авіамоторів. Високе значення вірогідності (0.997 чи 0.999) задається для всіх відповідальних наукових і технічних вимірювань, пов'язаних з можливими аварійними ситуаціями (наприклад. вимірювання параметрів роботи ядерних реакторів). В звичайних наукових дослідженнях і в студентській навчальній лабораторії достатньою вважається вірогідність

0.95.

Визначення надійного інтервалу.

Надійний інтервал випадкової похибки у випадку заданої вірогідності та невеликого числа вимірювань оцінюють за формулою:

x −∆p < x < x +∆p ,		(22)
де: ∆p =t p,k σ	1
де: ∆p =t p,k σ	k

t p,k − коефіцієнт, який залежить від вірогідності P та кількості

вимірювань і називається коефіцієнтом Стьюдента (див. табл. 2 додатку). В таблиці коефіцієнт Стьюдента шукають на перетині рядка, який відповідає відомому k , і стовпця, що визначає задану P ;

k = n −1 − число ступенів вільності;

σ − незміщена оцінка середньоквадратичного відхилення:

σ =	1	∑(xi − x)2 .
	n −1

Ця величина характеризує розподіл випадкових похибок за абсолютною величиною.

Як бачимо, похибка результату вимірювання визначається середньоквадратичним відхиленням середнього арифметичного σcp. = σn .

Отже, півширину надійного інтервалу випадкової похибки можна записати у вигляді:

∆	p	=t	p,k	σcp. .	(23)
	p		p,k

Приклад. Нехай для десяти вимірювань середнє значення та середньоквадратичне відхилення становлять x = 36.06 , σ = 0.25 відповідно. Оцінити істинне значення вимірюваної величини a з вірогідгністю P = 0.99 .

По заданій вірогідності та числу вимірювань n =10 , по таблиці 2 додатку знаходимо коефіцієнт Стьюдента t p,k = 3.25 ( k =9 ) і отримуємо оцінку

істинного значення a у вигляді:

a − x = a −36.06 < 3.25 0.259 = 0.27 ≈ 0.3 .

Таким чином, з вірогідністю P = 0.99 можна вважати, що значення a лежить в інтервалі (35.8;36.4).

2.4.3. Виключення “грубих” вимірів (промахів)

Промах - це значення, що сильно відрізняється від других вимірів. Тому вважають, якщо значення виміряної величини відрізняється від середньоарифметичного більше, ніж на 3σ , то його треба відкинути як промах.

2.4.4. Врахування інструментальної похибки та похибки заокруглення

Похибка вимірювання визначається похибкою приладу в тому випадку, коли виконується тільки одне спостереження (наприклад: вимірювання температури, зважування тіла, зчитування показів вольтметра). Разовим спостереженням обмежуються і тоді, коли три-чотири попередні вимірювання показують, що випадкова похибка не проявляється (при повторних вимірюваннях отримують один і той же результат). Це відбувається тоді, коли випадкова похибка є меншою за поріг чутливості приладу.

Гранична абсолютна похибка приладу Θnp. (максимально можлива похибка, обумовлена приладом) вказується в його паспорті або на шкалі

приладу. Якщо вказано клас точності приладу				K , то граничну		похибку
приладу визначають за формулою:
Θnp. =	K xmax	,		(24)

100
де xmax − максимальне значення,			яке даний прилад		може	виміряти
(якщо прилад має дві			шкали	відносно	нуля, то беруть

2xmax ).

Якщо клас точності приладу не відомий, то гранична похибка дорівнює 0.5 ціни поділки шкали.

При відомій вірогідності вимірювань P визначаємо похибку приладу:

∆np.	=tp	Θnp.	,	(25)
		3

де tp − коефіцієнт, поміщений в табл. 3 додатку.

При зчитуванні показів зі шкал приладів, часто виникає необхідність заокруглення показів до цілої поділки шкали. В такому разі похибку

заокруглення визначають за формулою:
∆3.	= P	h	,	(26)
		2

де h − ціна найменшої поділки.

При відсутності систематичної похибки визначають результуючу похибку прямих вимірювань:

∆ = ∆2p +∆np.2 +∆32. .

(27)

При записі кінцевого результату треба пам'ятати, що приведені формули для похибок достатньо точні при великих n . Якщо n ≤10, в надійному інтервалі результату вимірювання треба брати тільки одну значущу цифру.

Наприклад, при вимірюванні довжини мікрометром для n =10 отримали l = 6.033 мм, ∆ = 0.021 мм. ( P = 0.95 ). Результат запишеться:

l = 6.03 ±0.02 мм при P = 0.95 ; E = 0.3 %.

Такий запис означає, що істинне значення знаходиться між 6.01мм і 6.05мм з рівнем вірогідності 0.95, тобто результати приблизно 95% всіх вимірювань будуть знаходитись у вказаному інтервалі і тільки 5% вимірювань не ввійдуть в цей інтервал.

2.5. Похибки непрямих вимірювань

Здебільшого для визначення певної фізичної величини необхідно виміряти ряд інших величин; підставивши поміряні величини у відповідну формулу, знаходять шукану величину. Такі вимірювання називають непрямими.

Розглянемо, як визначають оцінку похибок непрямих вимірювань. Нехай фізична величина y є функцією декількох незалежно виміряних величин

x1, x2 ,..., xn : y = f (x1, x2 ,..., xn ).

Існують різні представлення похибок непрямих вимірювань. Знайдемо

повний диференціал функції: dy = ∑	∂ f	dxi . Аналогічний	вираз
повний диференціал функції: dy = ∑		dxi . Аналогічний	вираз
i ∂ x
	i
справедливий для малих приростів аргументів функції: ∆y = ∑∂ f			∆xi .
		i ∂xi

Якщо похибки вимірювань невеликі, то природньо вважати, що приріст аргумента рівний сумарній похибці відповідної величини вимірювань; тоді максимальну похибку непрямого вимірювання можна записати у вигляді:

∆y = ∑	∂ f ∆xi	.	(28)
i	∂xi

Формула (28) дає, здебільшого, сильно завищені значення похибки кінцевого результату, причому завищення зростає з числом виміряних величин. А тому вираз (28) використовують для невеликого числа змінних.

З другого боку, використавши закон додавання похибок [4, 5], для абсолютної похибки непрямих вимірювань можемо записати:

				1
			2
		∂f	2		2
		∂f		.		(29)

∆y = ∑		∂xi	∆xi
	i	∂xi

У формулі (29) найбільший внесок дають доданки з великими похибкими. Зауважимо, що похідні в (28), (29) беруться в точках x1, x2 ,..., xn .

Для прикладу розглянемо декілька часткових випадків:

а) y = x1 ± x2 .

Абсолютна похибка:

∆y =

(∆x1 )2

+ (∆x2 )2

;

∆x1 ,

∆x2 - результуючі

похибки.

(∆x1 )2 +(∆x2 )2

Відносна похибка: E =

∆y

(x ± x

)2 .

| y |

б) y = x1 x2 x3 .

Абсолютна похибка:

∆y = [(x2 x3 ∆x1 )2 +(x1 x3 ∆x2 )2 +(x1 x2 ∆x3 )2 ]

∆y

∆x1

∆x2

∆x3

Відносна похибка: E =

| y | =

в) y =

Абсолютна похибка: ∆y =

∆x1

x1∆x2

∆x2

Відносна похибка: E =

∆x1

Як бачимо, при обчисленні

похибки

добутків чи

частки простіше

спочатку порахувати відносну похибку E , а потім − абсолютну: ∆y = E | y |.

Дуже часто доводиться оперувати виразами, що містять добутки та частки вимірюваних величин. Оскільки такі вирази зручно логарифмувати, то при обчисленні похибок простіше спочатку визначати відносну похибку, а по

ній − абсолютну			(аналогічно до випадків б	та в). Справді, нехай
y =	x1 x 2 ... x k	.

	x k+1 ... x n		+... + ln xk − (ln xk +1 +... + ln xn ).
	Тоді: ln y = ln x1

Продиференціювавши останній вираз, отримуємо формулу для приростів:

dy	=	dx1	+... +	dxk
y		x
				x	k
	1

При малих n відносну співвідношенням (28):

			19

dxk +1				dxn
−		+... +			.
	xk +1
				xn
похибку			можна визначити за

∆y	=	∆x1	+... +	∆xn		.

y		x		x	n
		1

Отже, E = E1 +... + En .

Знаючи E , легко визначити абсолютну похибку.

2.6. Точність обчислень

Результати лабораторних вимірювань разом з довідковими даними, що використовуються при обробці експерименту, є приблизними величинами. Наближені числа записуються так, щоб всі цифри числа, крім останньої, були правильними (точними), а остання − сумнівною. Всі цифри справа від сумнівної будуть неправильними.

Щоб знати правильні, сумнівну і неправильні цифри числа, необхідно знати його похибку.

В таблицях математичних і фізичних величин приводять числа тільки з правильними цифрами і однією сумнівною; за максимальну похибку заокруглення беруть половину одиниці останньої цифри.

Наприклад, маса атома водню (див. таблицю фізичних сталих) становить

m =1.673 10−27 кг. Отже, похибка заокруглення рівна ±0.0005 10−27 кг. Значущими цифрами називають всі правильні і сумнівні цифри, а

незначущими − нулі напочатку числа, за допомогою яких задаються розряди десяткових дробів в числах, менших одиниці. Числа 0.25 , 0.025 , 0.0035 мають по дві значущі цифри.

При обробці результатів вимірювань треба пам'ятати, що точність обчислень повинна бути узгоджена з точністю самих вимірювань. Точність кінцевого результату визначається точністю безпосередньо виміряних величин. Немає сенсу проводити обчислення далі цієї межі точності, що забезпечується точністю початкових даних. Наприклад, якщо у формулі одна з величин визначена з точністю до двох значущих цифр, то немає змісту обчислювати результат з більшою точністю. Такі обчислення приводять до великого об'єму непотрібної роботи і тільки створюють ілюзію великої точності.

Іншими словами, числове значення результату не повинно мати більшого числа значущих цифр, ніж число, задане з найменшою точністю. Для уточнення значення останньої значущої цифри можна порахувати наступну за нею цифру і заокруглити результат.

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Соседние файлы в предмете Физика

#
03.05.20211.29 Mб1739.pdf
#
27.04.2021463.39 Кб0Obr_eksp_rez.pdf
#
27.04.2021720.98 Кб1Механіка.pdf
#
27.04.20211.1 Mб0Молекулярна фізика та темодинаміка.pdf
#
27.04.20214.08 Mб2Частина 1-2.pdf