Министерство науки и высшего образования Российской Федерации Калужский филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Московский государственный технический университет имени Н.Э. Баумана (Национальный Исследовательский Университет)» (КФ МГТУ им. Н.Э. Баумана)

ФАКУЛЬТЕТ	М-КФ «Машиностроительный»
КАФЕДРА	М10-КФ «Высшая математика»

ДОМАШНЯЯ РАБОТА №2

"Дифуравнения высшего порядка"

Вариант 21

ДИСЦИПЛИНА:	"Интегралы и дифференциальные уравнения"

Выполнил: студент гр. РПД.Б.-21	_______________(Прудников А. Ф.) Подпись Ф.И.О.
Проверил:	_______________(Беляев В. А. ) Подпись Ф.И.О.

Дата сдачи (защиты):
Результаты сдачи (защиты): -Балльная оценка -Оценка

Калуга, 2020 г.

Задача №1

Определите тип дифуравнения и найдите его общее решение.

Решение: Сначала определим тип дифуравнения. Данное уравнение является дифуравнением допускающим понижения порядка. Воспользуемся следующими формулами и .

Подставим данные в первую функцию:

;

Подведем под дифференциал и подставим в уравнение :

;

Теперь воспользуемся второй формулой:

;

Рассмотрим . В знаменателе выразим полный квадрат:

Подведем под дифференциал и подставим в уравнение:

Таким образом мы получаем следующее уравнение:

.

Задача №2

Определите тип дифуравнения и найдите его общее решение.

Решение: Сначала определим тип дифуравнения. Данное уравнение является дифуравнением второго порядка не содержащие в явном виде х. Поэтому понижение степени достигается следующим методом

Подставляя в начальное уравнение получим:

Преобразуем уравнение:

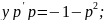
Проинтегрируем полученное уравнение:

Правая часть этого выражения – табличная, её результат . Рассмотрим левую часть . Подведем под дифференциал , подставим в выражение и найдём первообразную:

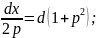
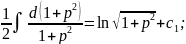
Получим выражение:

Пропотенцируем и преобразуем его:

Отсюда:

Преобразуем уравнение и проинтегрируем его:

Правая часть выражения является табличной и её интеграл равен Рассмотрим левую часть выражения 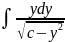. Подставим под знак дифференциала и получим Подставим в интеграл и найдём его:

Таким образом ответ будет выглядеть следующим образом:

Задача №3

Определите тип дифуравнения и найдите его общее решение.

Решение: Сначала определим тип дифуравнения. Данное уравнение является линейным неоднородным дифуравнением с постоянным коэффициентом и его общее решение может быть записано в виде , где – общее решение данного данного уравнения, – общее решение соответствующего однородного уравнения , - частное решение данного неоднородного уравнения.

Сначала найдём . Для этого составим характеристическое уравнение и найдём корни этого уравнения.

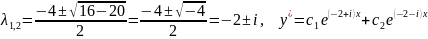
Преобразуем полученное общее решение с помощью следующих двух формул: и :

;

Частное решение будем находить методом Лагранжа (методом вариации произвольных постоянных), т.е.

Для нахождения и составим систему:

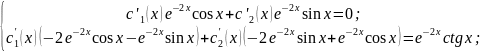
Сокращая на , получим:

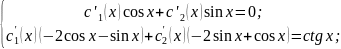
Полученную систему решим методом Крамера

Таким образом частное решение имеет вид

Общее решение примет вид

Задача №4

Определите тип дифуравнения и найдите его частное решение, удовлетворяющее начальным условиям: .

Решение: Сначала определим тип дифуравнения. Данное уравнение является линейным неоднородным дифуравнением второго порядка. Решение общего вида будет записываться в виде где – общее решение соответствующего однородного уравнения , а - частное решение.

Составим характеристическое уравнение:

.

Отсюда .

Таким образом, общее решение, учитывая формулы и .

Рассмотрим правую часть начального уравнения . Приравняем коэффициенты при соответствующих степенях и составим систему уравнений:

Выражения для подставляем в данное уравнение:

В полученном тождестве приравниваем коэффициенты при одинаковых степенях

Таким образом .

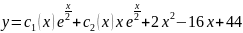Учитывая начальные условия

Учитывая начальные условия, .

Ответ: .