Министерство науки и высшего образования Российской Федерации Калужский филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Московский государственный технический университет имени Н.Э. Баумана (Национальный Исследовательский Университет)» (КФ МГТУ им. Н.Э. Баумана)

ФАКУЛЬТЕТ	М-КФ «Машиностроительный»
КАФЕДРА	М10-КФ «Высшая математика»

ДОМАШНЯЯ РАБОТА №1

"Определенный интеграл"

Вариант 21

ДИСЦИПЛИНА:	"Интегралы и дифференциальные уравнения"

Выполнил: студент гр. РПД.Б.-21	_______________(Прудников А. Ф.) Подпись Ф.И.О.
Проверил:	_______________(Беляев В. А. ) Подпись Ф.И.О.

Дата сдачи (защиты):
Результаты сдачи (защиты): -Балльная оценка -Оценка

Калуга, 2020 г.

1. Вычислить площадь фигуры, ограниченной кривой у=ln х, прямыми х=е, y=0.

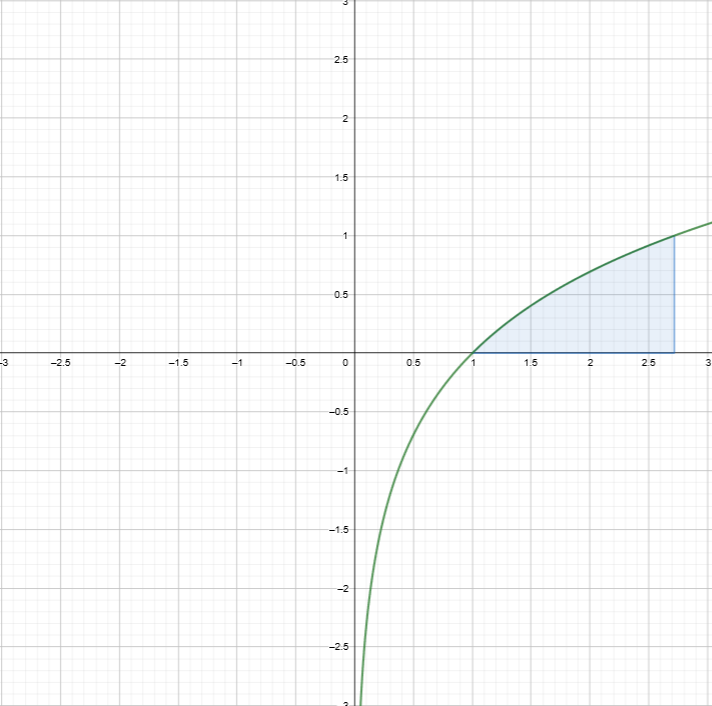
График функции пересекается с осью OY в точке х=1. Площадь фигуры находится по следующей формуле (1):

;

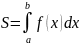Воспользуемся методом интегрирования по частям:

.

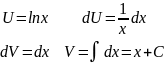
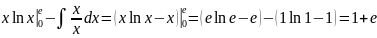2. Н айти объём тела, полученного при вращении вокруг оси OХ фигуры, ограниченной у=3(х-5)², у=0, х=0.

;

Объем тела вращения находим по формуле (8):

;

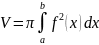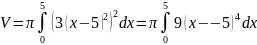
Подведем 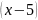под знак дифференциала:

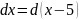
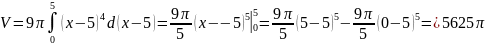
3. Найти длину одного витка кривой х =а cos 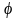, у =а sin , z = .

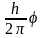Продифференцируем переменные:

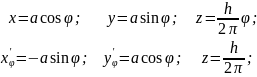
Запишем рабочую формулу (12):

.

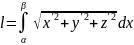
Обратим внимание, что под корнем основное тригонометрическое тождество и константа. Таким образом получим:

.

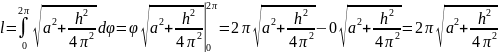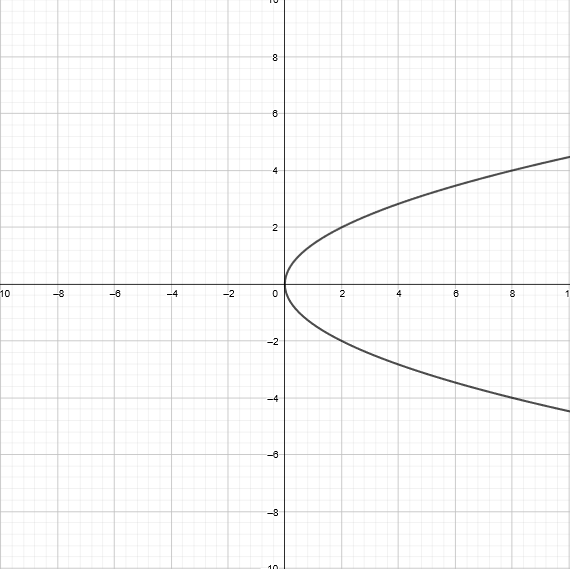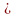4. В ычислить площадь поверхности части параболоида вращения, полученного при вращении части параболы у²=2rx, (0 x a) вокруг оси OX.

Преобразуем формулу функции и найдём производную от неё:

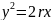
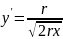
Запишем рабочую формулу (14):

.

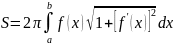
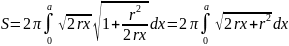Подведем под дифференциал :

.
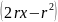
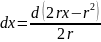
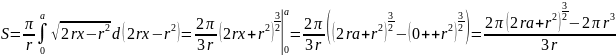