Метод поиска
Служит для выбора алгоритма оптимизации— метод Ньютона или сопряженных градиентов — для указания направление поиска.
Метод Ньютона. Реализация квазиньютоновского метода, в котором запрашивается больше памяти, но выполняется меньше итераций, чем в методе сопряженных градиентов.
Метод сопряженных градиентов. Реализация метода сопряженных градиентов, в котором запрашивается меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно велика и необходимо экономить память, а также если итерации дают слишком малое отличие в последовательных приближениях.
Загрузить модель
Служит для отображения на экране диалогового окна Загрузить модель, в котором можно задать ссылку на область ячеек, содержащих загружаемую модель.
Сохранить модель
Служит для отображения на экране диалогового окна Сохранить модель, в котором можно задать ссылку на область ячеек, предназначенную для хранения модели оптимизации. Данный вариант предусмотрен для хранения на листе более одной модели оптимизации — первая модель сохраняется автоматически.
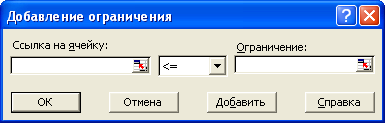
Рисунок 1.3 - Элементы диалоговых окон "Добавить" ограничение и "Изменить" ограничение
Ссылка на ячейку
Служит для указания ячейки или диапазона, на значения которых необходимо наложить ограничение.
Ограничение
Служит для задания условия, которое накладывается на значения ячейки или диапазона, указанного в поле Ссылка на ячейку. Выберите необходимый условный оператор ( <=, =, >=, Int или Bin ). Введите ограничение — число, формулу, ссылку на ячейку или диапазон — в поле справа от раскрывающегося списка.
Добавить
Нажмите на кнопку, чтобы, не возвращаясь в окно диалога Параметры поиска решения, наложить новое условие на поиск решения задачи.
3. Общий подход к построению регрессионной зависимости методом наименьших квадратов на примере линейной модели
Рассмотрим, как решается задача оптимизации с помощью средства Поиск решения на примере построения линейного уравнения регрессии.
Имеются две наблюдаемые величины x и y, например, объем реализации фирмы, торгующей подержанными автомобилями, за шесть недель ее работы. Значения этих наблюдаемых величин приведены в таблице 3.1, где х – отчетная неделя, а y – объем реализации за эту неделю.
Таблица 1.1 – Значения наблюдаемых величин
x |
1 |
2 |
3 |
4 |
5 |
6 |
y |
7 |
9 |
12 |
13 |
14 |
17 |
Необходимо получить уравнение регрессии данной зависимости.
Идеальное уравнение регрессии должно достаточно точно представлять экспериментальные данные и одновременно быть достаточно простым, т. е. иметь как можно меньше коэффициентов. Понятно, что не всегда удается удовлетворить этим двум, вообще говоря, противоречивым условиям, поэтому часто приходится жертвовать или простотой формулы, или ее точностью.
Остановимся на линейной модели y=mx+b, наилучшим образом описывающую наблюдаемые значения.
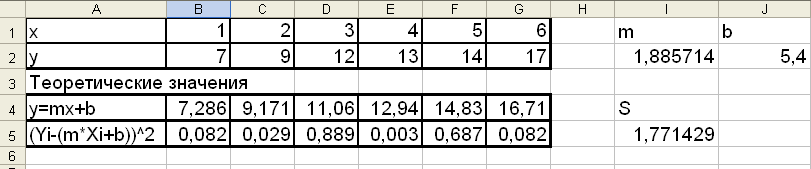
Рисунок 1.4 – Нахождение в Excel значений параметров уравнения регрессии
Согласно методу наименьших квадратов, m и b подбирают так, чтобы минимизировать
где n – число наблюдений.
Для решения этой задачи отведем под параметры m и b ячейки I2 и J2 соответственно. А в ячейку I5 введем минимизирующую функцию по формуле:
=СУММ(B5:G5).
При этом предполагаем m=1 и b=1.
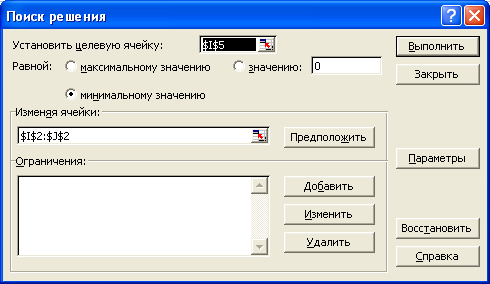
Рисунок 1.5 – Диалоговое окно Поиск решения
Минимизирующую функцию можно также ввести как = СУММКВРАЗН(B2:G2:C7;B4:G4). Функция СУММКВРАЗН вычисляет сумму квадратов разностей для элементов указанных массивов.
Теперь выберем команду Сервис-Поиск решения и заполним открывшееся диалоговое окно Поиск решения, как показано на рисунке 1.5
На рисунке 1.6 представлены графики данных и теоретических вычислений
Рисунок 1.6 – Графики данных и теоретических вычислений
Задание для лабораторной работы:
1 Используя метод наименьших квадратов (МНК), построить уравнения регрессии для заданного варианта. (Линейную и нелинейную (квадратичную, кубическую) зависимости).
2 Построить графики экспериментальных и полученных теоретических данных.
3 Сравнить результаты.
Таблица 1.2 – Варианты заданий
.
№ варианта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
№ задач |
1,11 |
2,10 |
3,9 |
4,8 |
1,7 |
2,6 |
3,5 |
4,6 |
2,5 |
4,9 |
1,8 |
3,11 |
4,5 |
1,3 |
3,7 |
1 Изменение коэффициента подачи насоса гидросистемы подъема кузова автосамосвала МАЗ
Пробег самосвала, тыс.км. |
40 |
80 |
120 |
160 |
200 |
240 |
280 |
320 |
360 |
Коэффициент подачи, Кф |
0,98 |
0,97 |
0,96 |
0,92 |
0,87 |
0,75 |
0,58 |
0,47 |
0,41 |
2.Количество газов, прорывающихся в картер двигателя при номинальной частоте вращения коленчатого вала для двигателя ЯМЗ-240
Пробег автомобиля, тыс.км. |
50 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
Количество газов |
90 |
92 |
87 |
95 |
97 |
110 |
150 |
200 |
3 Изменение массы осадка в роторе центрифуги дизельного двигателя
Наработка двигателя, мото-час |
100 |
200 |
300 |
400 |
500 |
600 |
Масса осадка,г |
50 |
108 |
165 |
220 |
272 |
310 |
4.Изменение давления в гидросистеме самосвала при подъеме кузова МАЗ5551 с сыпучим материалом
Высота подъема, м |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
Давление, Мпа |
4,95 |
6 |
6,8 |
7,5 |
8 |
7,6 |
6,9 |
4,6 |
1,5 |
5. Плотность асфальтобетона в зависимости от времени уплотнения
Время уплотнения, мин |
0,5 |
0,8 |
1 |
1,5 |
1,8 |
2 |
2,4 |
2,7 |
3 |
Плотность асфальтобетона, т/м3 |
1,5 |
1,8 |
2,07 |
2,18 |
2,39 |
2,45 |
2,46 |
2,48 |
2,5 |
6.Плотность грунта от количества проходов катка
Количество проходов катка |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
24 |
28 |
30 |
Плотность грунта, т/м3 |
1,5 |
1,7 |
1,78 |
1,9 |
1,99 |
2,01 |
2,09 |
2,09 |
2,1 |
2,07 |
2,09 |
2,1 |
7 Дальность отбрасывания снега в зависимости от угла наклона ротора снегоочистителя
Наклон ротора, град |
0 |
10 |
15 |
25 |
30 |
45 |
55 |
60 |
70 |
80 |
90 |
Дальность отбрасывания, м |
1 |
7 |
13 |
20 |
23 |
25 |
24 |
21 |
16 |
10 |
1 |
8.Сила сопротивления перемещению транспортной машины в зависимости от угла подъема дороги.
Угол подъема, град. |
0 |
2 |
3 |
4 |
5 |
7 |
8 |
9 |
10 |
11 |
12 |
Сила сопротивления, кН |
100 |
107 |
110 |
113 |
117 |
124 |
127 |
131 |
134 |
137 |
140 |
9.Время цикла экскаватора от угла поворота экскаватора.
Угол поворота, град. |
0 |
15 |
30 |
45 |
60 |
90 |
110 |
130 |
150 |
170 |
180 |
Время цикла, с |
10 |
16 |
21 |
26 |
29 |
32 |
34 |
34 |
33 |
34 |
35 |
10. Время погрузки самосвала в зависимости от вместимости ковша экскаватора.
Вместимость ковша, м3 |
0,2 |
0,4 |
0,5 |
0,7 |
0,8 |
1 |
1,1 |
1,3 |
1,4 |
1,5 |
1,6 |
Время погрузки, c |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
200 |
220 |
250 |
270 |
11. Зависимость удельной производительности сит от размера ячеек.
Размер сит |
0,42 |
1,5 |
3,4 |
10,2 |
15,3 |
17,6 |
20,3 |
23,7 |
25,4 |
Удельная производительность, т/(м2·ч) |
0 |
15,3 |
34 |
42 |
46 |
56 |
57,5 |
62,4 |
64,5 |