4.2. Двухбарьерные структуры

Современные технологические методы позволяют создать гетероструктуры с толщиной 1÷ 10 нм. Эта толщина может быть сравнима с длиной волны де Бройля электронов и дырок, поэтому в таких структурах может проявляться волновая природа носителей заряда, в частности открывается возможность резонансного туннелирования электронов через систему ям и барьеров.

U U1 z 0 a1 a1+L a1+ a2+L U2 E

Рис. 4.3. Двухбарьерная квантовая структура

Пусть на двухбарьерную структуру (рис. 4.3) в положительном направлении оси падают электроны с энергиейи импульсом.

Найдем амплитуды отражения и прохождения(,, гдеипо-прежнему обозначают коэффициенты отражения и прохождения), не решая уравнение Шредингера, а рассматривая многократные отражения волн от барьеров. Амплитуды отраженияи прохождениядля первого и второго барьеров соответственно считаем известными. Учитывая, что фазовый набег электронной волны при распространении от одного барьера до другого равен, и суммируя получающиеся геометрические прогрессии, можно написать

.

Обозначим , тогда коэффициент прохождения

. (4.8)

Если импульс падающих частиц удовлетворяет условию

, (4.9)

то их коэффициент прохождения

. (4.10)

Подчеркнем, что зависят от, причем, как можно показать, в интересующем нас случае туннелирования через прямоугольные барьеры.

Будем считать барьеры достаточно толстыми. В этом случае амплитуды прохождения иэкспоненциально малы (, где), аамплитуды отражения близки по модулю к единице:

. (4.11)

Подставляя это выражение в (4.10), получим

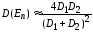, (4.12)

где . В частности, приимеем. Это и естьэффект резонансного туннелирования. Поскольку число частиц при рассеянии на барьере сохраняется, то .

Итак, хотя проницаемости барьеров малы (), при некоторых значениях энергии частица не чувствует барьеров. Механизм резонансного туннелирования таков: из-за интерференции электронных волн при их отражении от барьеров снаружи остаются лишь падающая и прошедшая волны, а обратная (отраженная) волна полностью гасится.

Полезно найти волновую функцию электрона в яме между барьерами. Она имеет вид

(4.13)

где

(4.14)

Здесь амплитуда падающей волны считается равной 1. Из формул (4.14) видно, что при .

Полагая , получаем. Таким образом, амплитуда волновой функции внутри ямы значительно больше, чем вне барьерной структуры. На языке классической механики можно сказать, что электрон задерживается в яме на большой промежуток времени и многократно рассеивается на барьерах, вследствие чего многократно возрастает вероятность его туннелирования из ямы.

Отметим одно довольно важное обстоятельство. После формулы (4.12) приведены значения уровней энергии в пространстве между барьерами в виде. Но нужно отдавать себе отчет, что если электрон обладает вероятностью выхода частицы из межбаръерной ямы, то энергия уровней должна быть комплексной величиной, т.е. вместо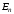мы должны иметь. Мнимую часть энергии уровня можно сопоставить с его полушириной, которую, в свою очередь, можно найти из соотношение неопределенности. Таким образом, вместо энергии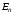будем окончательно иметь, где мы формально положили. С учетом этого обстоятельства, после достаточно громоздкой, хотя принципиально и не сложной алгебры можно прийти к выражению

. (4.15)

_{Так как появившийся энергетический множитель не превышает единицы, я}сно, что в общем случае и .

Пространственные флуктуации толщины или состава барьерных слов приводят к тому, что на различных участках двухбарьерной структуры энергии резонансных уровней различны, что в свою очередь уменьшает полный резонансный ток частиц с заданной энергией. Поэтому требование высокой степени идентичности и однородности барьерных слоев является существенным при изготовлении резонансных туннельных гетероструктур и приборов на их основе. В качестве последнотметим резонансно-туннельные диоды.