
- •Введение
- •Часть I
- •Глава 1. Квантовые ямы
- •1.1. Одномерные изолированные квантовые ямы
- •Прямоугольная потенциальная яма
- •Треугольная потенциальная яма
- •Параболическая потенциальная яма
- •Плотность состояний в одномерных квантовых ямах
- •1.2. Двумерные и трехмерные изолированные квантовые ямы
- •1.2.1. Потенциальный ящик с бесконечными стенками
- •1.2.2. Потенциальный цилиндр
- •1.2.3. Потенциальный параллелепипед
- •1.2.4. Потенциальная сфера
- •Кулоновская яма
- •Сдвоенные квантовые ямы
- •Дираковская потенциальная гребенка
- •Вакансия в дираковской потенциальной гребенке
- •Полубесконечная дираковская потенциальная гребенка
- •Задачи к гл. 1
- •Глава 2. Решеточные модели низкоразмерных систем
- •2.1. Метод функций Грина
- •2.2. Однозонная модель линейной цепочки
- •2.3. Двухзонная модель линейной цепочки
- •2.4. Одноатомная плоская решетка
- •2.5. Трехмерные системы с пространственным квантованием
- •2.6. О плотностях состояний бесструктурных систем пониженной размерности
- •Задачи к гл. 2
- •Глава 3. Особенности фононного спектра наносистем
- •3.1. Простейшие модели колебаний атомов в твердых телах
- •3.2. Колебания одно- и двухатомных цепочек
- •3.2.1. Одноатомная цепочка
- •3.2.2. Двухатомная цепочка
- •3.3. Изотопический дефект в одноатомной линейной цепочке
- •3.4. Вакансия в одноатомной линейной цепочке
- •3.5. Интерфейсные фононы в полярных кристаллах
- •Задачи к гл. 3
- •Глава 4. Туннелирование через квантово-размерные структуры
- •4.1. Коэффициент прохождения
- •4.2. Двухбарьерные структуры
- •4.3. Кулоновская блокада туннелирования
- •4.3.1. Общие соотношения
- •4.3.2. Потенциальная энергия гранулы
- •4.3.3. Вольт-амперная характеристика
- •Задачи к гл. 4
Задачи к гл. 2
2.1.
Исходя из уравнения Шредингера получить
секулярное уравнение (2.3) и найти
коэффициенты
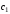 и
и (воспользоваться стандартным
квантово-механическим подходом).
(воспользоваться стандартным
квантово-механическим подходом).
Указание.
При нахождении значений коэффициентов
 и
и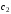 учесть, что
учесть, что .
.
2.2. Получить выражение (2.21).
2.3. Построить график энергетической плотности состояний (2.31) для однозонной модели линейной цепочки.
2.4. С учетом выражений (2.34) и (2.35) построить энергетическую диаграмму для двухзонной модели линейной цепочки.
Указание. Первоначально построить законы дисперсии для зон проводимости и валентной, а затем спроектировать края зон на ось энергий, получить полосы разрешенных и запрещенных состояний; определить энергии краев полос.
2.5. Воспользовавшись выражениями (2.39) и результатами задачи 2.3, построить закон дисперсии и энергетическую плотность состояний двухзонной модели линейной цепочки.
2.6.
Используя уравнения Дайсона, найти
функции Грина, энергетические уровни
и локальные плотности состояний атомов
в линейной эквидистантной трехатомной
цепочке, построенной из одинаковых
атомов с энергиями орбиталей
 и связанных потенциалом
и связанных потенциалом .
.
2.7.
То же, что и задача 2.6, но для атомов,
расположенных в вершинах равностороннего
треугольника и связанных друг с другом
потенциалом
 .
Проанализировать отличие полученных
результатов от 2.6.
.
Проанализировать отличие полученных
результатов от 2.6.
Тема семинара: «Методы расчета зонной структуры твердых тел»
Глава 3. Особенности фононного спектра наносистем
3.1. Простейшие модели колебаний атомов в твердых телах
Для
простейшего описания колебаний атомов
около их положений равновесия используется
модель Эйнштейна, согласно которой
каждый атом колеблется независимо от
других подобно простому гармоническому
осциллятору в потенциальной яме,
образованной силами его взаимодействия
с соседями. При этом спектр возбуждений
кристалла состоит из эквидистантных
уровней, расположенных на расстоянии
 друг от друга, где
друг от друга, где − эйнштейновская частота, т. е. частота
осцилляций каждого атома в своей
потенциальной яме. Плотность состояний
для такой модели
− эйнштейновская частота, т. е. частота
осцилляций каждого атома в своей
потенциальной яме. Плотность состояний
для такой модели .
.
Модель Эйнштейна весьма груба и работает лишь при высоких температурах, когда предположение о независимости колебаний различных атомов оправдано. Сразу видно, однако, что если два или более атомов движутся в унисон, то силы между ними, стремящиеся возвратить эти атомы в положение равновесия, уменьшаются и, следовательно, квант энергии возбуждения будет несколько меньше. Существует тенденция к корреляции движений соседних атомов.
Так как в модели
Эйнштейна рассматривается независимый
осциллятор, то речи о волне, возбуждаемой
в кристалле, не идет. Поэтому не встает
вопрос о волновых векторах
 и о дисперсии колебаний. Отсюда следует,
что эйнштейновское описание значительно
лучше подходит к оптическим фононам с
малой дисперсией, нежели к акустическим
фононам, испытывающим значительную
дисперсию.
и о дисперсии колебаний. Отсюда следует,
что эйнштейновское описание значительно
лучше подходит к оптическим фононам с
малой дисперсией, нежели к акустическим
фононам, испытывающим значительную
дисперсию.
Для простейшего описания акустических фононов используется модель Дебая, которая строится на следующих предположениях.
Считается, что все акустические колебания характеризуются одинаковой скоростью звука s:
 .
(3.1)
.
(3.1)
Зону Бриллюэна заменют сферой. Это означает, что существует максимальная частота колебаний решетки – дебаевская частота
 ,
соответствующая радиусу этой сферы.
Радиус сферы легко найти, замечая, что
она должна содержать точноN
точек при плотности их в q-пространстве,
равной
,
соответствующая радиусу этой сферы.
Радиус сферы легко найти, замечая, что
она должна содержать точноN
точек при плотности их в q-пространстве,
равной
 (
( −
объем кристалла). Соответственно, должно
выполняться следующее равенство:
−
объем кристалла). Соответственно, должно
выполняться следующее равенство:
 ,
(3.2)
,
(3.2)
где
 – объем элементарной ячейки, откуда
– объем элементарной ячейки, откуда
 ,
(3.3)
,
(3.3)
Тогда спектральная плотность состояний принимает вид
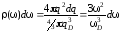 ,
(3.4)
,
(3.4)
где
 есть дебаевская частота.
есть дебаевская частота.
Модель
Дебая хорошо работает при вычислении
теплоемкости кристалла, давя при высоких
температурах
 ,
где
,
где −
температура Дебая, дает для теплоемкости
закон Дюлонга – Пти
−
температура Дебая, дает для теплоемкости
закон Дюлонга – Пти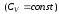 ,
а при низких температурах
,
а при низких температурах − кубическому закону
− кубическому закону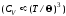 .
.
Формула
Дебая оправдывается для большинства
твердых тел, а температура Дебая дает
масштаб температуры: величина
 представляет максимальный квант энергии,
способный возбудить колебания решетки.
Кроме того, температура
связана со средней скоростью звука s
в кристалле соотношением
представляет максимальный квант энергии,
способный возбудить колебания решетки.
Кроме того, температура
связана со средней скоростью звука s
в кристалле соотношением
 .
.
Отметим, что обе рассмотренные нами простейшие модели колебаний в твердых телах бесструктурны. Чтобы понять свойства колебаний решетки, полезно изучить несколько простых, но учитывающих структуру системы случаев.
