Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ»

кафедра физики

Л А Б О Р А Т О Р Н А Я Р А Б О Т А № 2

ИССЛЕДОВАНИЕ

ДИНАМИКИ ГАРМОНИЧСКИХ КОЛЕБАНИЙ

В ПОЛЕ СИЛЫ ТЯЖЕСТИ

Санкт-Петербург, 2012

РАБОТА №2

ИССЛЕДОВАНИЕ ДИНАМИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ

В ПОЛЕ СИЛЫ ТЯЖЕСТИ

Цель работы: изучение закономерностей колебательного движения тела в однородном силовом поле; исследование процессов превращения энергии в консервативных системах; определение момента инерции физического маятника.

Приборы и принадлежности: оборотный маятник; секундомер; масштабная линейка, чертежный треугольник.

Конструкция оборотного маятника представлена на рис. 1. На стержне 1 закреплены два диска – D₁ и D₂. Маятник может быть подвешен на кронштейне к одной из легких призм P₀, P₁, P₂, трение в которых пренебрежимо мало.

Исследуемые закономерности

Физический маятник –­ это тело с распределенной массой или система тел, ось вращения которого расположена выше центра масс маятника. Относительно этой оси маятник колеблется с периодом

(1)

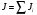
где для составного маятника масса маятника, положение его центра масс относительно оси вращения, и масса i-го тела и положение его центра масс относительно оси вращения, полный момент инерции маятника,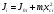 – момент инерции i-го тела, рассчитанный относительно оси вращения по теореме Штейнера, момент инерции этого тела относительно его центра масс. Величина называется приведенной длиной физического маятника.

Полный момент инерции маятника может быть представлен в ви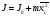де , где 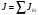, средний квадрат положений центров масс системы тел, составляющих маятник.

Если период колебаний маятника определен экспериментально, то из (1) можно найти момент инерции маятника .

Сохранение энергии гармонических колебаний. Поскольку физический маятник, качающийся под действием силы тяжести, является консервативной системой, можно проанализировать процесс перехода потенциальной энергии маятника в кинетическую.

Максимальная потенциальная энергия маятника равна

(5)

где высота поднятия ЦМ маятника при его максимальном отклонении от положения равновесия, 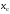– положение ЦМ маятника относительно его точки подвеса, максимальный угол отклонения маятника от положения равновесия.

Максимальная кинетическая энергия физического маятника

, (6)

где момент инерции маятника выражен по формуле (1) через период его колебаний. Из закона сохранения полной механической энергии

можно найти максимальную угловую скорость маятника при прохождении им положения равновесия .

Задание по подготовке к работе:

1. Изучите описание лабораторной работы.

2. Подготовьте бланк «Протокола наблюдений» (формат А4).

3. Разработайте Таблицу результатов наблюдений времени n = 10 колебаний маятника при его подвешивании к призме . Таблицу занесите в протокол наблюдений. Число опытов по определению времени колебаний для каждой призмы равно 10. Приборные погрешности времен колебания маятника запишите в крайний правый столбец таблицы.

4. В данной работе для нахождения результата косвенного измерения рационально использовать метод переноса погрешностей. Используя формулу , выведите формулу расчета полной погрешности результата измерения момента инерции маятника в методе переноса погрешностей. При выводе формулы рекомендуется использовать метод логарифмирования функции.

Указания по выполнению наблюдений

1. Убедиться, что стержень маятника параллелен вертикальной стойке кронштейна. Если это не соблюдается, то выровнять основание маятника таким образом, чтобы стержень был параллелен стойке с укрепленной на ней линейкой.

2. Записать в «Протокол наблюдений» с панели установки массу маятника m, длину l и диаметр d стержня, диаметры и толщины 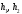дисков, плотность материал , из которого изготовлены элементы маятника.

3. Пододвинуть призму P₂ вплотную к призме P₁ и закрепить ее. Положить маятник на стол и измерить относительно вершины призмы P₂ положения центров масс дисков и середины стержня. Результаты записать в протокол.

4. Положить маятник на ребро призмы и найти положение центра масс маятника (точку его равновесия). Его положение относительно вершины призмы P₂ записать в протокол.

5. Подвесить оборотный маятник на призме P₂. Отклонить маятник на угол, составляющий примерно 5° - это соответствует совпадению образующей верхнего диска маятника с вертикальной кромкой линейки кронштейна. С помощью чертежного треугольника и линейки шкалы на стойке кронштейна определить катеты для угла отклонения маятника . Отпустить маятник и измерить с помощью секундомера время, за которое маятник совершает n = 10 колебаний. Записать время колебаний t_0i в подготовленную таблицу протокола наблюдений. Повторить эти измерения 10 раз.

6. Записать приборную погрешность измерения времени в протокол.

Задание по обработке результатов измерений

1. По данным таблицы рассчитать методом переноса погрешностей среднее значение периода колебаний маятника T₀ и полную доверительную погрешность результата измерения. Записать результат косвенного измерения периода колебаний маятника в стандартной форме.

2. Пользуясь методом средних (переноса погрешностей), рассчитать среднее значение момента инерции маятника J, а по формуле, полученной в подготовке к работе, его полную погрешность измерения. Результат записать в стандартной форме, округлив его.

3. Используя измеренные значения параметров и в пп.4 и 5 указаний по выполнению наблюдений, рассчитайте по формуле (5) полную механическую энергию маятника .

4. Рассчитайте приведенную длину маятника .

5. Используя данные п. 2 указаний по выполнению наблюдений, рассчитайте массы стержня и дисков маятника. Сопоставьте сумму этих масс с полной массой маятника, указанной на панели установки.

6. Используя предыдущий п. 7 и п. 3 указаний по выполнению наблюдений, рассчитайте положение центра масс маятника и сопоставьте его со значением определенным экспериментально.

7. Используя данные п. 3 указаний по выполнению наблюдений и п. 5, рассчитайте по теореме Штейнера моменты инерции каждого из тел составного маятника и его полный момент инерции. Сопоставьте его значение с определенным экспериментально в п. 2.

Контрольные вопросы

1. Какие колебания называют гармоническими? Объясните смысл требования малости угловой амплитуды колебаний маятника.

2. Какой маятник называют физическим, а какой математическим?

3. Что такое приведенная длина физического маятника? Как ее определить экспериментально?

4. С одинаковыми или разными угловыми и линейными ускорениями и скоростями движутся различные точки маятника при его колебаниях

5. Какие законы используются для описания колебаний физического маятника?

6. Напишите уравнение движения для гармонического осциллятора и объясните физический смысл величин, входящих в это уравнение.

7. Покажите, что максимальные кинетическая и потенциальная энергии тела, колеблющегося по гармоническому закону, совпадают с его полной механической энергией

8. Дайте определение центра масс системы тел.

9. Дайте определение моментов инерции материальной точки и составного тела.

10. Сформулируйте теорему Штейнера.