ГУАП

КАФЕДРА № 41

ОТЧЕТ

ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

старший преподаватель				Е.П. Виноградова
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №5

Симплекс-метод

по курсу: Прикладные методы оптимизации

РАБОТУ ВЫПОЛНИЛА

СТУДЕНТКА ГР.	4716				С.А. Янышева
			подпись, дата		инициалы, фамилия

Санкт-Петербург

2020

Лабораторная работа № 5 Симплекс-метод

1. Цель работы

Симплексный метод применяется при решении задач линейного программирования, заданных в канонической форме. Приобрести практические навыки решения задач линейного программирования симплекс методом.

2. Вариант задания

Вариант 3

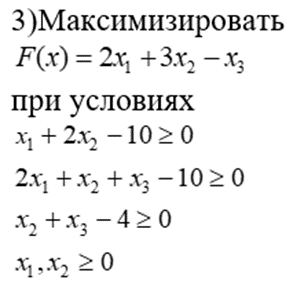
3. Ход выполнения работы

Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).

В 1-м неравенстве смысла (≥) вводим базисную переменную x₄ со знаком минус. В 2-м неравенстве смысла (≥) вводим базисную переменную x₅ со знаком минус. В 3-м неравенстве смысла (≥) вводим базисную переменную x₆ со знаком минус. В 4-м неравенстве смысла (≥) вводим базисную переменную x₇ со знаком минус. В 5-м неравенстве смысла (≥) вводим базисную переменную x₈ со знаком минус.

x₁+2x₂-x₄ = 10

2x₁+x₂+x₃-x₅ = 10

x₂+x₃-x₆ = 4

x₁-x₇ = 0

x₂-x₈ = 0

Расширенная матрица системы ограничений-равенств данной задачи:

1	2	0	-1	0	0	0	0	10
2	1	1	0	-1	0	0	0	10
0	1	1	0	0	-1	0	0	4
1	0	0	0	0	0	-1	0	0
0	1	0	0	0	0	0	-1	0

Приведем систему к единичной матрице методом жордановских преобразований.

1. В качестве базовой переменной можно выбрать x₄.

Получаем новую матрицу:

-1	-2	0	1	0	0	0	0	-10
2	1	1	0	-1	0	0	0	10
0	1	1	0	0	-1	0	0	4
1	0	0	0	0	0	-1	0	0
0	1	0	0	0	0	0	-1	0

2. В качестве базовой переменной можно выбрать x₅.

Получаем новую матрицу:

-1	-2	0	1	0	0	0	0	-10
-2	-1	-1	0	1	0	0	0	-10
0	1	1	0	0	-1	0	0	4
1	0	0	0	0	0	-1	0	0
0	1	0	0	0	0	0	-1	0

3. В качестве базовой переменной можно выбрать x₆.

Получаем новую матрицу:

-1	-2	0	1	0	0	0	0	-10
-2	-1	-1	0	1	0	0	0	-10
0	-1	-1	0	0	1	0	0	-4
1	0	0	0	0	0	-1	0	0
0	1	0	0	0	0	0	-1	0

4. В качестве базовой переменной можно выбрать x₇.

Получаем новую матрицу:

-1	-2	0	1	0	0	0	0	-10
-2	-1	-1	0	1	0	0	0	-10
0	-1	-1	0	0	1	0	0	-4
-1	0	0	0	0	0	1	0	0
0	1	0	0	0	0	0	-1	0

5. В качестве базовой переменной можно выбрать x₈.

Получаем новую матрицу:

-1	-2	0	1	0	0	0	0	-10
-2	-1	-1	0	1	0	0	0	-10
0	-1	-1	0	0	1	0	0	-4
-1	0	0	0	0	0	1	0	0
0	-1	0	0	0	0	0	1	0

Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (4,5,6,7,8).

Выразим базисные переменные через остальные:

x₄ = x₁+2x₂-10

x₅ = 2x₁+x₂+x₃-10

x₆ = x₂+x₃-4

x₇ = x₁

x₈ = x₂

Подставим их в целевую функцию:

F(X) = 2x₁+3x₂-x₃

Среди свободных членов b_i имеются отрицательные значения, следовательно, полученный базисный план не является опорным.

Вместо переменной x₄ следует ввести переменную x₂.

Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.

Базис	B	x1	x2	x3	x4	x5	x6	x7	x8
x2	5	1/2	1	0	-1/2	0	0	0	0
x5	-5	-3/2	0	-1	-1/2	1	0	0	0
x6	1	1/2	0	-1	-1/2	0	1	0	0
x7	0	-1	0	0	0	0	0	1	0
x8	5	1/2	0	0	-1/2	0	0	0	1
F(X0)	-15	1/2	0	-1	3/2	0	0	0	0

Представим расчет каждого элемента в виде таблицы:

B	x1	x2	x3	x4	x5	x6	x7	x8
-10 : -2	-1 : -2	-2 : -2	0 : -2	1 : -2	0 : -2	0 : -2	0 : -2	0 : -2
-10-(-10 • -1):-2	-2-(-1 • -1):-2	-1-(-2 • -1):-2	-1-(0 • -1):-2	0-(1 • -1):-2	1-(0 • -1):-2	0-(0 • -1):-2	0-(0 • -1):-2	0-(0 • -1):-2
-4-(-10 • -1):-2	0-(-1 • -1):-2	-1-(-2 • -1):-2	-1-(0 • -1):-2	0-(1 • -1):-2	0-(0 • -1):-2	1-(0 • -1):-2	0-(0 • -1):-2	0-(0 • -1):-2
0-(-10 • 0):-2	-1-(-1 • 0):-2	0-(-2 • 0):-2	0-(0 • 0):-2	0-(1 • 0):-2	0-(0 • 0):-2	0-(0 • 0):-2	1-(0 • 0):-2	0-(0 • 0):-2
0-(-10 • -1):-2	0-(-1 • -1):-2	-1-(-2 • -1):-2	0-(0 • -1):-2	0-(1 • -1):-2	0-(0 • -1):-2	0-(0 • -1):-2	0-(0 • -1):-2	1-(0 • -1):-2

Среди свободных членов b_i имеются отрицательные значения, следовательно, полученный базисный план не является опорным.

Вместо переменной x₅ следует ввести переменную x₄.

Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.

Базис	B	x1	x2	x3	x4	x5	x6	x7	x8
x2	10	2	1	1	0	-1	0	0	0
x4	10	3	0	2	1	-2	0	0	0
x6	6	2	0	0	0	-1	1	0	0
x7	0	-1	0	0	0	0	0	1	0
x8	10	2	0	1	0	-1	0	0	1
F(X1)	-30	-4	0	-4	0	3	0	0	0

Представим расчет каждого элемента в виде таблицы:

B	x1	x2	x3	x4	x5	x6	x7	x8
5-(-5 • -1/2):-1/2	1/2-(-11/2 • -1/2):-1/2	1-(0 • -1/2):-1/2	0-(-1 • -1/2):-1/2	-1/2-(-1/2 • -1/2):-1/2	0-(1 • -1/2):-1/2	0-(0 • -1/2):-1/2	0-(0 • -1/2):-1/2	0-(0 • -1/2):-1/2
-5 : -1/2	-11/2 : -1/2	0 : -1/2	-1 : -1/2	-1/2 : -1/2	1 : -1/2	0 : -1/2	0 : -1/2	0 : -1/2
1-(-5 • -1/2):-1/2	1/2-(-11/2 • -1/2):-1/2	0-(0 • -1/2):-1/2	-1-(-1 • -1/2):-1/2	-1/2-(-1/2 • -1/2):-1/2	0-(1 • -1/2):-1/2	1-(0 • -1/2):-1/2	0-(0 • -1/2):-1/2	0-(0 • -1/2):-1/2
0-(-5 • 0):-1/2	-1-(-11/2 • 0):-1/2	0-(0 • 0):-1/2	0-(-1 • 0):-1/2	0-(-1/2 • 0):-1/2	0-(1 • 0):-1/2	0-(0 • 0):-1/2	1-(0 • 0):-1/2	0-(0 • 0):-1/2
5-(-5 • -1/2):-1/2	1/2-(-11/2 • -1/2):-1/2	0-(0 • -1/2):-1/2	0-(-1 • -1/2):-1/2	-1/2-(-1/2 • -1/2):-1/2	0-(1 • -1/2):-1/2	0-(0 • -1/2):-1/2	0-(0 • -1/2):-1/2	1-(0 • -1/2):-1/2

Выразим базисные переменные через остальные:

x₂ = -2x₁-x₃+x₅+10

x₄ = -3x₁-2x₃+2x₅+10

x₆ = -2x₁+x₅+6

x₇ = x₁

x₈ = -2x₁-x₃+x₅+10

Подставим их в целевую функцию:

F(X) = 2x₁+3(-2x₁-x₃+x₅+10)-x₃

Или

F(X) = -4x₁-4x₃+3x₅+30

2x₁+x₂+x₃-x₅=10

3x₁+2x₃+x₄-2x₅=10

2x₁-x₅+x₆=6

-x₁+x₇=0

2x₁+x₃-x₅+x₈=10

При вычислениях значение Fc = 30 временно не учитываем.

Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:

2	1	1	0	-1	0	0	0
3	0	2	1	-2	0	0	0
2	0	0	0	-1	1	0	0
-1	0	0	0	0	0	1	0
2	0	1	0	-1	0	0	1

Базисные переменные - это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.

Решим систему уравнений относительно базисных переменных: x₂, x₄, x₆, x₇, x₈. Полагая, что свободные переменные равны 0, получим первый опорный план:

X0 = (0,10,0,10,0,6,0,10)

Базисное решение называется допустимым, если оно неотрицательно. 

Базис	B	x1	x2	x3	x4	x5	x6	x7	x8
x2	10	2	1	1	0	-1	0	0	0
x4	10	3	0	2	1	-2	0	0	0
x6	6	2	0	0	0	-1	1	0	0
x7	0	-1	0	0	0	0	0	1	0
x8	10	2	0	1	0	-1	0	0	1
F(X0)	0	4	0	4	0	-3	0	0	0

Переходим к основному алгоритму симплекс-метода.

Окончательный вариант симплекс-таблицы:

Базис	B	x1	x2	x3	x4	x5	x6	x7	x8
x2	10	2	1	1	0	-1	0	0	0
x4	10	3	0	2	1	-2	0	0	0
x6	6	2	0	0	0	-1	1	0	0
x7	0	-1	0	0	0	0	0	1	0
x8	10	2	0	1	0	-1	0	0	1
F(X1)	0	4	0	4	0	-3	0	0	0

Последняя строка содержит отрицательные элементы. Пространство допустимых решений неограниченно. Решения не существует.

4. Выводы

При выполнении лабораторной работы был изучен Симплекс-метод. Было выяснено, что симплексный метод применяется при решении задач линейного программирования, заданных в канонической форме. Были приобретены практические навыки решения задач линейного программирования симплекс методом.