ГУАП

КАФЕДРА № 41

ОТЧЕТ

ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

старший преподаватель				Е.П. Виноградова
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №2

Сравнение методов одномерной оптимизации

по курсу: Прикладные методы оптимизации

РАБОТУ ВЫПОЛНИЛА

СТУДЕНТКА ГР.	4716				С.А. Янышева
			подпись, дата		инициалы, фамилия

Санкт-Петербург

2020

Лабораторная работа № 2

Сравнение методов одномерной оптимизации

1. Цель работы

Определение сравнительной эффективности методов одномерной оптимизации.

2. Вариант задания

Вариант 3

Функция Ф(x)	Интервал [a; b]	Погрешность определения экстремума εx
3		[- ]

3. Аналитический расчет точки экстремума

y = cos(x + π)

y’ = -sin(x + π)

-sin(x + π) = 0

x = πn

Если x∈[- ] ⇒ x = 0

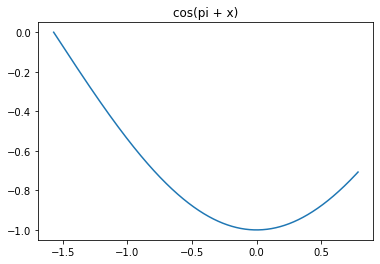
Рисунок 1 – График функции y = cos(x + π)

4. Краткие теоретические сведения

   1. Алгоритм равномерного поиска

Алгоритм равномерного поиска заключается в том, что испытания проводятся в точках, определяемых путём равномерного деления интервала допустимых значений [a; b] на Т одинаковых интервалов. Затем из вычисленных значений Ф(x) выбирается наименьшее – пусть оно достигается в точке х_k. Тогда, поскольку Ф(x) унимодальна, то интервалы [a; x_k-1] и [x_k+1; b] из рассмотрения можно исключить. Таким образом, за интервал неопределенности будет принят интервал [x_k-1; x_k+1].

2. Метод дихтомии

Алгоритм дихотомии (также алгоритм деления пополам, алгоритм равномерного дихотомического поиска) – простейший метод одномерной оптимизации, который относится к классу методов последовательного поиска. В алгоритме дихотомии испытания проводятся парами в середине ТИН. На каждом шаге поиска ТИН делится пополам. Далее вычисляется значение функции Ф(х) в окрестности [х-δ; х+δ]. По значениям Ф(х-δ) и Ф(х+δ) одна половина ТИН отбрасывается за счет унимодальности функции.

3. Метод золотого сечения

Метод золотого сечения относится к последовательным методам поиска. Рассмотрим интервал [a; b]. Считается, что точка с удовлетворяет условию золотого сечения, если выполняется соотношение:

где 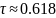– решение квадратного уравнения

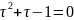
Отсюда следует выражение:

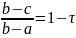
Алгоритм золотого сечения можно представить в виде такого порядка действий:

1. Выполнить присваивания r = 1, a⁽¹⁾=a, b⁽¹⁾=b, ТИН1=[a⁽¹⁾; b⁽¹⁾];

2. Вычислить величины: x₁^(r) = b^(r) – (b^(r) – a^(r))τ; x₂^(r) = a^(r) + (b^(r) – a^(r))τ;

3. Вычислить значения Ф(x₁^(r)), Ф(x₂^(r));

4. Если Ф(x₁^(r)) < Ф(x₂^(r)),то выполнить присваивание a^(r+1)=a^(r), b^(r+1)=x₂^(r), ТИН_r+1=[a^(r+1); b^(r+1)]; иначе – выполнить присваивание a^(r+1)=x₁^(r), b^(r+1)=b^(r), ТИНr+1=[ a^(r+1); b^(r+1)];

5. Сравнить |ТИН_r+1| и ε_x, где ε_x – требуемая погрешность вычисления;

6. Если выполняется условие (1), то закончить вычисления. Иначе – выполнить присваивание r=r+1 и повторить п.2 – 6.

4. Метод Фибоначчи

Метод Фибоначчи относится к классу поисковых методов оптимизации и состоит из двух этапов.

На первом этапе производится (N-1)-й итераций для r=1, 2… N-1.

1. Рассмотрим общий алгоритм выполнения r-той итерации, где ТИНr=[a(r); b(r)]:

2. Вычислить значения:

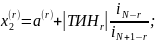
3. Вычислить значения Ф(x₁^(r)), Ф(x₂^(r));

4. Если Ф(x₁^(r)) < Ф(x₂^(r)), то выполнить присваивание a^(r+1)=a^(r), b^(r+1)=x2^(r), ТИН_r+1=[a^(r+1); b^(r+1)]; иначе – выполнить присваивание a^(r+1)=x₁^(r), b^(r+1)=b^(r), ТИН_r+1=[a^(r+1); b^(r+1)].

Второй этап осуществляется по следующему принципу:

1. Найти точку x^(N)=x^(N-1)+ δ, где δ << |ТИН_N-1| – свободный параметр алгоритма.

2. Вычислить значение Ф(x^(N));

3. Если Ф(x^(N)) < Ф(x^(N–1)), то выполнить присваивание ТИН_N=[a^(N-1); x^(N-1)]; иначе – выполнить присваивание ТИНN=[x^(N-1); b^(N-1)].

В качестве приближенного значения точки минимума x* c равными основаниями принимается любая точка ТИН_N.

5. Результаты работы методов

Листинг 1 – Код программы

import numpy as np

from matplotlib import pyplot as plt

writer = lambda a, b, steps: {'a':a,'b':b,'steps':steps}

f = lambda x0: np.cos(np.pi+x0)

eps = 2**(-15)

a = -np.pi/2

b = np.pi/4

eps0 = [[],[],[],[]]

res = []

#1Алгоритм равномерного поиска

n = 50

steps = 0

a1, b1 = a, b

while (abs(b1-a1) > eps):

x = np.arange(a1, b1, (b1-a1)/n)

vals = [f(i) for i in x[0:-1]]

ch = vals.index(min(vals))

a1, b1 = x[ch-1], x[ch+1]

steps += 1

eps0[0].append(b1-a1)

res.append(writer(a1, b1, steps))

#2 Алгоритм дихтомии(алгоритм деления пополам)

steps = 0

a1, b1 = a, b

while (abs(b1-a1) > eps):

n = (a1+b1)/2

x = [(a1+n)/2, (b1+n)/ 2]

vals = [f(i) for i in x]

if vals[0] < vals[1]:

b1 = n

else:

a1 = n

steps += 1

eps0[1].append(b1-a1)

res.append(writer(a1, b1, steps))

#3 Метод золотого сечения

steps = 0

a1, b1 = a, b

while (abs(b1-a1) > eps):

x = [b1-(b1-a1)*0.618, a1+(b1-a1)*0.618]

vals = [f(i) for i in x]

if vals[0] < vals[1]:

b1 = x[1]

else:

a1 = x[0]

steps += 1

eps0[2].append(b1-a1)

res.append(writer(a1, b1, steps))

#4 Метод Фибоначчи

steps = 1

a1, b1 = a, b

fib = [1, 1]

while ((b1 - a1) / fib[-1] > eps):

fib.append(fib[-2] + fib[-1])

while (abs(b1-a1) > eps):

x = [a1 + (b1 - a1) * (fib[len(fib) - 1 - steps] / fib[len(fib) - steps]),

a1 + (b1 - a1) * (fib[len(fib) - 1 - steps] / fib[len(fib) - steps])]

if x[0] == x[1]:

x[1] = x[0] + (b1 - a1)/10

vals = [f(i) for i in x]

if vals[1] < vals[0]:

a1 = x[0]

else:

b1 = x[1]

steps += 1

eps0[3].append(b1-a1)

res.append(writer(a1, b1, steps-1))

lbls = ['Алгоритм равномерного поиска', 'Метод дихтомии', 'Метод золотого сечения',

'Метод Фибоначчи']

[print(lbls[i],'\n',res[i]) for i in range(len(res))]

plt.plot(range(res[0]['steps']),eps0[0], label = lbls[0])

plt.plot(range(res[1]['steps']),eps0[1], label = lbls[1])

plt.plot(range(res[2]['steps']),eps0[2], label = lbls[2])

plt.plot(range(res[3]['steps']),eps0[3], label = lbls[3])

plt.legend()

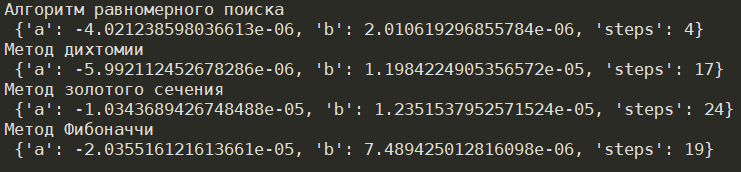
Рисунок 2 – Результат работы программы

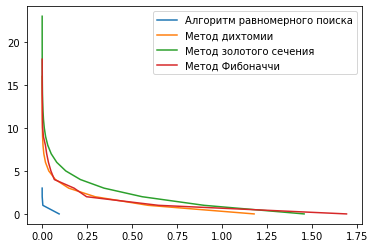
Рисунок 3 – Графики зависимости числа итераций от погрешности для всех методов

6. Выводы

В результате выполнения лабораторной работы были изучены различные методы одномерной оптимизации, а также оценена их эффективность и трудоемкость. В результате получилось, что наименее трудоемким для заданного варианта оказался алгоритм равномерного поиска, который потребовал всего 4 итерации для нахождения минимума на интервале. Наиболее трудоемкими оказались методы золотого сечения и метод Фибоначчи, которым потребовалось 24 и 19 итераций. Из данных наблюдений можно сделать вывод, что наименее трудоемким и наиболее эффективным в данном случае является алгоритм равномерного поиска.
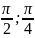