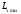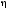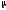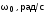- •2.1. Основные сведения
- •2.2. Программа работы
- •2.2.1. Исследование влияния контурного коэффициента усиления системы на ее динамические свойства
- •2.2.2. Исследование влияния относительной инерционности звеньев системы на ее устойчивость
- •2.2.3. Изучение стандартных полиномов и диаграммы Вышнеградского
- •2.3. Содержание отчета
- •2.4. Контрольные вопросы
2.2. Программа работы
Работа рассчитана на два занятия: программа первого включает задания 2.2.1 и 2.2.2, второго – 2.2.3.
2.2.1. Исследование влияния контурного коэффициента усиления системы на ее динамические свойства
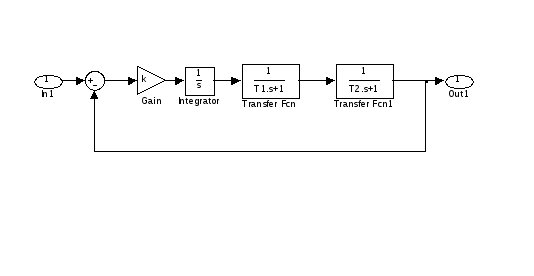
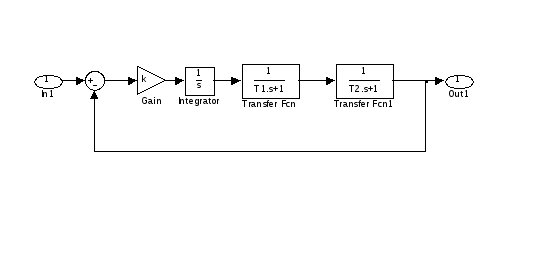
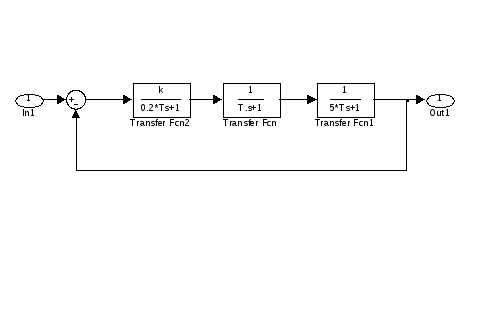
1. Задать структурную
схему системы третьего порядка,
составленную из последовательно
соединенных звеньев с ПФ
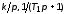 и
и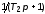 ,
охваченных единичной отрицательной
обратной связью. Назначить
,
охваченных единичной отрицательной
обратной связью. Назначить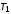 в соответствии с нижеприведенными
вариантами и задать
в соответствии с нижеприведенными
вариантами и задать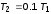 :
:
|
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
1.0 |
0.1 |
2.0 |
0.2 |
2.5 |
0.25 |
0.8 |
0.5 |
0.4 |
4.0 |
2. Для значений
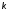 ,
равных
,
равных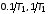 и
и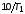 ,
определить и занести в таблицу значения
,
определить и занести в таблицу значения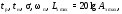 корней ХП,
корней ХП,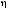 и
и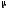 .
Описать изменение характера переходного
процесса с увеличением
.
Описать изменение характера переходного
процесса с увеличением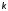 .
.
|
|
0.1/Т1 |
1/Т1 |
10/Т1 |
|
tp |
110 |
34 |
|
|
tн |
110 |
14.7 |
|
|
|
0 |
21% |
|
|
|
0 |
1.9 |
|
|
|
0 |
|
|
|
корни ХП |
0, -2.5; 0, -0.219; 0, -0.0285 |
|
|
|
|
0.0285 |
|
|
|
|
0 |
|
|
3. Увеличить
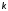 до значения
до значения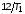 .
Ответить на вопросы: каким стал переходный
процесс? какие изменения произошли с
корнями ХП?
.
Ответить на вопросы: каким стал переходный
процесс? какие изменения произошли с
корнями ХП?
4. Разомкнуть
обратную связь. Для значений
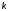 ,
указанных в пп. 2 и 3, определить и занести
в таблицу
,
указанных в пп. 2 и 3, определить и занести
в таблицу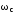 и (только для первых трех значений
и (только для первых трех значений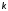 )
)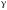 ,
а также исследовать с позиций критерия
Найквиста изменения, происходящие в
АФХ и ЛЧХ с ростом
,
а также исследовать с позиций критерия
Найквиста изменения, происходящие в
АФХ и ЛЧХ с ростом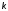 .
.
2.2.2. Исследование влияния относительной инерционности звеньев системы на ее устойчивость
5. В предыдущей
схеме, но с замкнутой обратной связью
и со значением
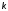 ,
назначенном в п. 3, уменьшить
,
назначенном в п. 3, уменьшить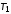 в 4 раза. Описать изменения, произошедшие
в характере переходного процесса и в
расположении корней ХП.
в 4 раза. Описать изменения, произошедшие
в характере переходного процесса и в
расположении корней ХП.
6. Задать структурную
схему системы, состоящей из трех
последовательно соединенных апериодических
звеньев с постоянными времени
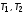 и
и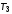 ,
охваченных единичной отрицательной
обратной связью. Одно из звеньев имеет
коэффициент передачи
,
охваченных единичной отрицательной
обратной связью. Одно из звеньев имеет
коэффициент передачи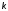 ,
остальные – единичный.
,
остальные – единичный.
7. Назначить
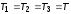 ,
где
,
где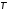 – произвольная константа. Подобрать
такое значение
– произвольная константа. Подобрать
такое значение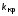 контурного коэффициента
контурного коэффициента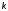 ,
при котором система выйдет на колебательную
границу устойчивости, т. е. ПХ примет
вид незатухающих колебаний. Определить
частоту
,
при котором система выйдет на колебательную
границу устойчивости, т. е. ПХ примет
вид незатухающих колебаний. Определить
частоту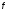 ,
Гц, этих колебаний.
,
Гц, этих колебаний.
8. Назначить
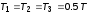 .
Снова определить
.
Снова определить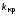 и
и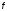 ,
сравнить их с предыдущими значениями.
,
сравнить их с предыдущими значениями.
9. Оставив
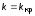 ,
задать новое соотношение постоянных
времени:
,
задать новое соотношение постоянных
времени: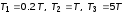 .
Охарактеризовать изменения, произошедшие
в свойствах системы. Увеличением
.
Охарактеризовать изменения, произошедшие
в свойствах системы. Увеличением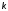 определить новое значение
определить новое значение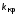 .
.
10. По результатам исследований в пп. 5–9 ответить на вопрос: какие факторы – абсолютные значения постоянных времени или их соотношения – влияют на устойчивость, характер переходных процессов в системе и на ее критический коэффициент усиления ?
2.2.3. Изучение стандартных полиномов и диаграммы Вышнеградского
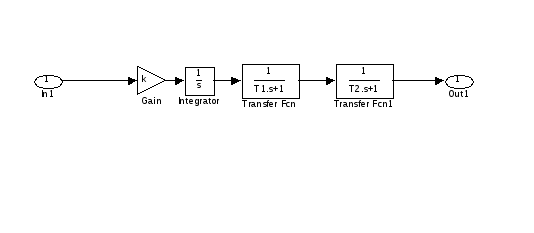
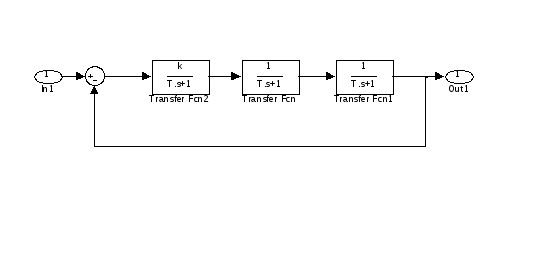
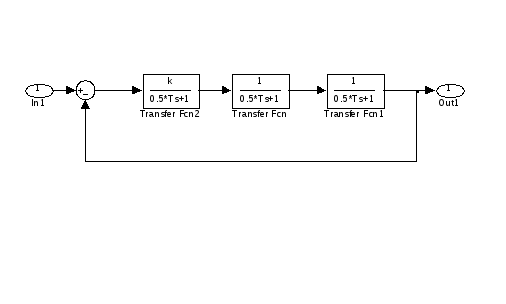
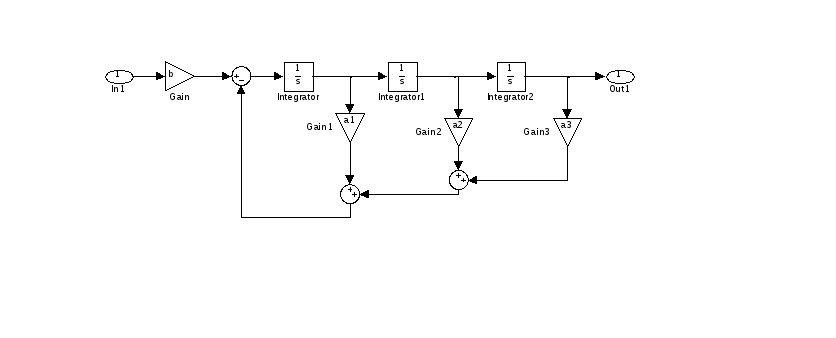
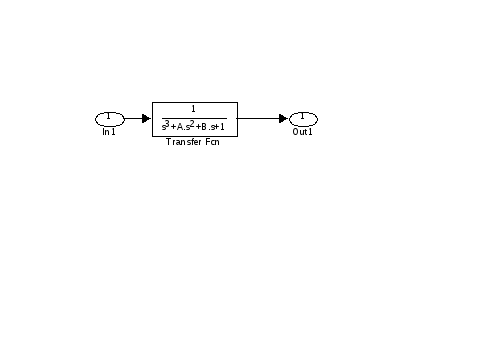
11. Задать структурную схему системы третьего порядка в управляемой канонической форме (рисунок).
12. Задать систему
с единичным коэффициентом передачи и
ХП Баттерворта,
для чего назначить
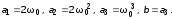 Значение
Значение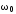 взять из приведенных ниже:
взять из приведенных ниже:
|
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
1 |
10 |
2 |
5 |
4 |
2,5 |
3 |
20 |
8 |
12 |
13. Определить корни
ХП и установить закономерность их
геометрического расположения на
комплексной плоскости. Определить
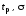 и
и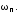
14. Повторить анализ,
увеличив
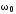 в 2 раза.
в 2 раза.
15. Задать систему
с биномиальным
ХП, назначив
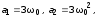
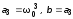 (оставить
первоначальное значение
(оставить
первоначальное значение
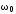 )
и повторить п. 13.
)
и повторить п. 13.
16. Задать звено с
ПФ
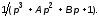
|
Параметр |
Номер опыта | |||||
|
1 |
2 |
3 |
4 |
5 |
6 | |
|
A |
0.5 |
1 |
3 |
2 |
5 |
6 |
|
B |
0.5 |
1 |
3 |
5 |
2 |
6 |
17. Последовательно
задавать комбинации значений параметров
Вышнеградского
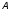 и
и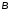 согласно таблице. Для каждого из сочетаний
определить полюсы ПФ и описать характер
ПХ.
согласно таблице. Для каждого из сочетаний
определить полюсы ПФ и описать характер
ПХ.

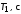
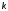

 п
п