
- •2.1. Основные сведения
- •2.2. Программа работы
- •2.2.1. Исследование влияния контурного коэффициента усиления системы на ее динамические свойства
- •2.2.2. Исследование влияния относительной инерционности звеньев системы на ее устойчивость
- •2.2.3. Изучение стандартных полиномов и диаграммы Вышнеградского
- •2.3. Содержание отчета
- •2.4. Контрольные вопросы
2.1. Основные сведения
Важнейшими
показателями
качества
(ПК) переходной
характеристики
(ПХ)
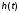 ,
илипрямыми
показателями качества
системы являются:
,
илипрямыми
показателями качества
системы являются:
время регулирования
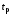 – время, по истечении которого ПХ не
выходит из области допустимых (обычно
пятипроцентных) отклонений от
установившегося значения (УЗ)
– время, по истечении которого ПХ не
выходит из области допустимых (обычно
пятипроцентных) отклонений от
установившегося значения (УЗ)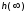 :
: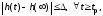 где
где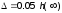 ;
;время нарастания

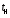 – время первого достижения УЗ;
– время первого достижения УЗ;перерегулирование

 – превышение максимума ПХ над УЗ в
процентах от УЗ:
– превышение максимума ПХ над УЗ в
процентах от УЗ: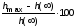 .
.
Среди косвенных ПК систем автоматического управления широко употребляются частотные и корневые.
Некоторые частотные ПК:
частота среза
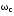 – частота, при которой ЛАХ разомкнутой
системы пересекает ось абсцисс:
– частота, при которой ЛАХ разомкнутой
системы пересекает ось абсцисс: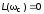 ;
служит мерой быстродействия системы;
;
служит мерой быстродействия системы;запас устойчивости по фазе
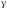 – превышение ЛФХ разомкнутой системы
на частоте среза над уровнем –
– превышение ЛФХ разомкнутой системы
на частоте среза над уровнем –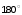 (в устойчивой системе):
(в устойчивой системе):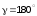 +
+
+
+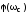 ;
с уменьшением
;
с уменьшением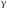 переходные процессы становятся более
колебательными;
переходные процессы становятся более
колебательными;полоса пропускания
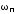 – частота, при которой значение АЧХ
замкнутой системы в
– частота, при которой значение АЧХ
замкнутой системы в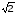 раз меньше ее значения на нулевой
частоте:
раз меньше ее значения на нулевой
частоте: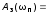
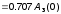 или
или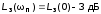 ;
является мерой быстродействия системы;
;
является мерой быстродействия системы;показатель колебательности
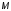 – отношение максимального значения
АЧХ замкнутой системы к начальному
значению:
– отношение максимального значения
АЧХ замкнутой системы к начальному
значению: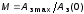 ;
характеризует склонность системы к
колебаниям.
;
характеризует склонность системы к
колебаниям.
Основные корневые ПК:
степень устойчивости
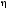 – расстояние от мнимой оси до ближайшего
корня (или пары комплексно-сопряженных
корней) характеристического полинома
(ХП) замкнутой системы; является мерой
быстродействия; если ПФ не имеет нулей,
то при увеличении действительной и
мнимой частей каждого полюса в
– расстояние от мнимой оси до ближайшего
корня (или пары комплексно-сопряженных
корней) характеристического полинома
(ХП) замкнутой системы; является мерой
быстродействия; если ПФ не имеет нулей,
то при увеличении действительной и
мнимой частей каждого полюса в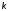 раз длительность переходного процесса
сократится также в
раз длительность переходного процесса
сократится также в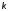 раз;
раз;колебательность
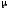 – отношение модулей мнимой и вещественной
частей ближайшей к мнимой оси пары
комплексных корней ХП; чем больше
– отношение модулей мнимой и вещественной
частей ближайшей к мнимой оси пары
комплексных корней ХП; чем больше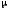 ,
тем меньше затухание колебаний за
период.
,
тем меньше затухание колебаний за
период.
Некоторые способы суждения об устойчивости системы:
для асимптотической устойчивости необходимо и достаточно, чтобы все корни ХП располагались в левой полуплоскости; если один корень находится в начале координат или одна пара корней – на мнимой оси (остальные – в левой полуплоскости), то система находится на границе устойчивости – соответственно, апериодического или колебательного типа);
в асимптотически устойчивой системе все коэффициенты ХП положительны; если хотя бы один из коэффициентов ХП отрицателен, система неустойчива;
согласно критерию Гурвица, для асимптотической устойчивости системы третьего порядка с положительными коэффициентами ХП необходимо и достаточно, чтобы произведение двух средних коэффициентов было больше произведения двух крайних коэффициентов (для колебательной границы устойчивости имеет место равенство этих произведений);
согласно критерию Найквиста, если ПФ разомкнутой системы имеет полюсы только в левой полуплоскости (кроме, возможно, одного нулевого), то для асимптотической устойчивости замкнутой системы необходимо и достаточно, чтобы при изменении частоты от нуля до бесконечности АФХ разомкнутой системы не охватывала точку с координатами (–1, j0), или, что то же самое, чтобы разность между числом положительных (сверху вниз) и отрицательных (снизу вверх) переходов АФХ через луч (
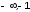 ]
равнялась нулю; в терминах ЛЧХ это
соответствует тому, что в диапазоне
частот, где ЛАХ разомкнутой системы
лежит выше оси, разность между числом
положительных (снизу вверх) и отрицательных
(сверху вниз) переходов ЛФХ через
горизонтальную прямую с ординатой
]
равнялась нулю; в терминах ЛЧХ это
соответствует тому, что в диапазоне
частот, где ЛАХ разомкнутой системы
лежит выше оси, разность между числом
положительных (снизу вверх) и отрицательных
(сверху вниз) переходов ЛФХ через
горизонтальную прямую с ординатой равняется нулю.
равняется нулю.
