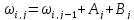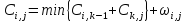Shpora
.docx●Задача коммивояжера – получаем в каждой строке и столбце по нулю и исключаем строку и столбец с самым тяжелым нулем. Самый тяжелый нуль тот, для которого сумма минимальных элементов в его строке и столбце максимальна, среди прочих кандидатов.
●Двойной обход МОД
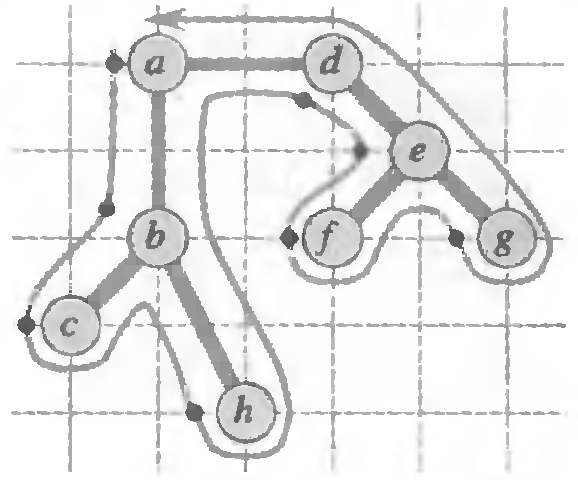
●Метод ближайшего соседа – всегда идем в ближайший город, кроме посещенных. Когда города закончатся – возвращаемся в начальный.
●Алгоритм начинается с маршрута, состоящего из одного произвольно выбранного города. Новый город, добавляемый на каждом шаге, выбирается из городов, еще не вошедших в маршрут, как город, ближайший к некоторому городу, уже принадлежащему маршруту; новый город тогда включается в маршрут следующим после того города из маршрута, который является ближайшим к нему.
●Задача о порядке перемножения матриц
![]()
●Количество операций при умножении матриц ы (n,m) на (m,k) равно n*m*k
●Слоистая сеть. Для каждой вершины, начиная с последней вычисляем волшебную функцию fn(s) (стоимость пути, по которому можно добраться из вершины s до финиша за n шагов), значение которой является минимум из сумм расстояний от предыдущей вершины до конечной. Значение функции на текущем шаге = минимум(путь из текущей вершины в следующую + fn-1(s)). fn-1(s) – это стоимость пути от n-1 вершины до конца.
●Оптимальная триангуляция выпуклого многоугольника. Берем a1. Находим минимальную диагональ a1-aj кроме an, проводим ее. Далее проводим диагональ aj-an. Применяем алгоритм для двух получившихся многоугольников.
●Оптимальные БДП