TR 2.6 var 19

ТР 2.6 Вариант 19

а) С точностью ε=0,001 найти суммы S_k рядов.

б) вычислить значение интеграла I с точностью ε=0,0001, разложить подынтегральную функцию в степенной ряд и проинтегрировав его почленно

1. Найти сумму ряда с точностью ε=0,001

Проверим сходимость ряда по признаку Коши. Для этого вычислим число K

Следовательно, ряд сходится по признаку Коши

Выберем число q, удовлетворяющее неравенству:

Значит можно взять q = 0,5

Решим неравенство:

Если обозначить , то можно показать, что y_n-1 > y_n т.е y_n монотонно убывает. Неравенство будем решать простым подбором. При n = 1 имеем:

Т.е. и в силу монотонного убывания y_n неравенство справедливо при n≥1. Положим N=1.

Решим неравенство . Так как q=1/2, то левая часть неравенства . Логарифмируя, получим:

Выберем m=10

Возьмем n₀ = max{N,m} = max{1,10} =10. Тогда |S₁ – S₁(10)| < ε. Вычислим непосредственно:

Значит с точностью ε=0,001 сумма ряда

2. Найти сумму ряда с точностью ε=0,001

Проверим сходимость ряда по признаку Даламбера. Для этого вычислим число D

Следовательно, ряд сходится по признаку Даламбера

Выберем число q, удовлетворяющее неравенству:

Значит можно взять q = 0,5

Подберем n удовлетворяющее неравенству:

При n=1:

Т.е. и в силу монотонного убывания неравенство справедливо при n≥1. Положим N=1.

Решим неравенство

Решение найдем простым подбором. Получаем m ≥ 9

Выберем m=9

Возьмем n₀ = max{N,m} = max{1,9} =9. Тогда |S₂ – S₂(9)| < ε. Вычислим непосредственно:

Значит с точностью ε=0,001 сумма ряда

3. Найти сумму ряда с точностью ε=0,001

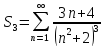
Рассмотрим функцию . Она положительна и убывает при x ≥ 1. Тогда:

Следовательно, ряд сходится по интегральному признаку Коши

Здесь и далее используется оценка:

Где a ≥ 1, b ≥ 1, c ≥ 0, d ≥ 2

Произведем интегральную оценку остатка ряда

Найдем наименьшее 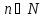, при котором

Т.е. n = 6. Тогда |S₃ – S₃(6)| < ε. Вычислим непосредственно:

Значит с точностью ε=0,001 сумма ряда

4. Вычислить значение интеграла I с точностью ε=0,0001, разложить подынтегральную функцию в степенной ряд и проинтегрировав его почленно

Разложим функции и 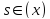в степенной ряд по степеням x:

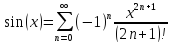
Тогда

Это разложение верно для x, таких что т.е. , следовательно степенной ряд равномерно сходится на отрезке [-,]. На отрезке равномерной сходимости ряд можно интегрировать почленно. Отсюда:

Где обозначено

Покажем, что ряд C(n) сходится, используя признак Лейбница:

Для доказательства неравенства a_n+1 > a_n при n ≥ 1, рассмотрим функцию:

определенную на [1, +∞), f(n) = a_n и докажем, что она убывает при всех x [1, +∞)

Так как функция f(x) является произведением положительных функций f₁(x)= и f₂(x)=, которые убывают на [1, +∞), то убывает на [1, +∞), т.е. для произвольных x₁ и x₂ [1, +∞), x₁ < x₂ справедливо равенство f(x₁) > f(x₂). Пусть x₁=n и x₂=n+1. Тогда a_n = f(x₁) > f(x₂) = a_n+1 для всех n>0 и требуемое неравенство установлено.

Ряд сходится в силу признака Лейбница.

Найдем наименьшее n при котором верно неравенство

Решение ищем простым перебором. При n=4 неравенство выполнено.

Вычислим непосредственно:

Аналогично находим:

Тогда интеграл

Значит интеграл с точностью