Функции / Дифференциалы / Понятие дифференциала функции

Понятие дифференциала функции

Пусть функция y = f(x) определена и дифференцируема в некоторой окрестности точки х₀ (рис. 3.28). тогда существует конечное значение производной:

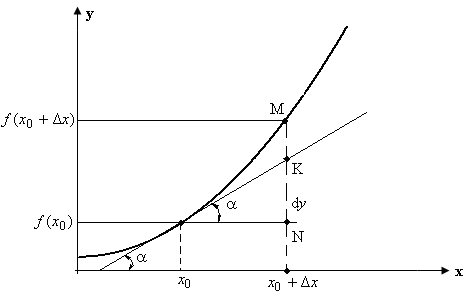
Рис. 3.28

Длина отрезка MN определяет приращение функции при приращении аргумента на Δх.

Обозначим длину KN через dy. Из прямоугольного треугольника tgα равен отношению катета противолежащего к катету прилежащему. Производная равна тангенсу угла наклона касательной tgα к оси 0х: = tgα

Значит длина отрезка KN будет равна:

На чертеже приращение функции Δу =MN, дифференциал функции dy= KN

Определение. Дифференциал функции dy равен произведению производной на приращение аргумента:

или dy = dх

Приращение аргумента Δх равно дифференциалу аргумента dх

Основные свойства дифференциала аналогичны свойствам производной функции.

Задача1. Найти дифференциал функции в точке х₀ = –1 при приращении аргумента Δх = 0,02.

Решение. Находим дифференциал функции:

Находим значение дифференциала при заданных значениях х₀ и Δх: