Министерство сельского хозяйства Российской Федерации
Федеральное государственное бюджетное
образовательное учреждение высшего образования
«Государственный университет по землеустройству»
Кафедра землепользования и кадастров
Практическая работа по статистике №2:
«Выборочный метод. Проверка статистических гипотез»
Выполнил:
Проверил:
Москва 2019
Задача 2.1 Точечная и интервальная оценка параметров генеральной совокупности по данным выборки
2.1.1. Точечная и интервальная оценка среднего значения признака в генеральной совокупности по данным большой выборки
Условие: имеются данные выборочного наблюдения за ценами за сотку (таблица 2.1.).
Требуется провести точечную и интервальную оценку среднего значения цены за сотку в этих районах.
Решение:
Определим квадраты значений признака (хi2) и запишем их в таблицу 2.1.
2.
Подсчитаем
и
и также запишем в таблицу 2.1.
Таблица 2.1. Цена за сотку, тыс. руб. по результатам выборочного наблюдения
№ наблю-дения |
Цена за сотку, тыс.руб. |
Квадрат |
№ наблю-дения |
Цена за сотку, тыс.руб. |
Квадрат |
||
значения |
значения |
||||||
признака |
признака |
||||||
Х i |
Х i2 |
Х i |
Х i2 |
||||
1 |
40,00 |
1600 |
16 |
357,14 |
127549 |
||
2 |
57,14 |
3264,98 |
17 |
83,33 |
6943,889 |
||
3 |
50,00 |
2500 |
18 |
236,36 |
55866,05 |
||
4 |
125,00 |
15625 |
19 |
148,72 |
22117,64 |
||
5 |
131,67 |
17336,99 |
20 |
203,57 |
41440,74 |
||
6 |
133,33 |
17776,89 |
21 |
70,00 |
4900 |
||
7 |
39,00 |
1521 |
22 |
440,00 |
193600 |
||
8 |
85,00 |
7225 |
23 |
118,64 |
14075,45 |
||
9 |
90,00 |
8100 |
24 |
86,30 |
7447,69 |
||
10 |
100,0 |
10000 |
25 |
44,44 |
1974,914 |
||
11 |
120,00 |
14400 |
26 |
83,33 |
6943,889 |
||
12 |
130,00 |
16900 |
27 |
40,74 |
1659,748 |
||
13 |
136,00 |
18496 |
28 |
29,33 |
860,2489 |
||
14 |
150,00 |
22500 |
29 |
90,00 |
8100 |
||
15 |
383,33 |
146941,9 |
30 |
440,00 |
193600 |
||
Итого |
4242,37 |
991267 |
|||||
Вычислим среднюю величину по данным выборочной совокупности:
(тыс.руб.)
Найдем выборочную дисперсию:
Исчислим несмещенную дисперсии:
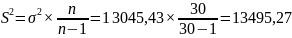
Рассчитаем среднюю ошибку выборочной средней для случайного бесповторного отбора:
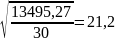(тыс.руб.)
Примечание:
так как число выборки по отношению к
числу единиц генеральной совокупности
чрезвычайно мало, то поправочным
коэффициентом
можно пренебречь.
Проведем точечную оценку средней в генеральной совокупности:
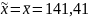(тыс.руб.)
при m
x
=
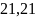тыс.руб
По таблице "Значение интеграла вероятностей при разных значениях t" найдем теоретическое значение t при доверительном уровне вероятности
:
t0,95=1,96.Определим предельную случайную ошибку выборочной средней:
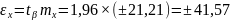(тыс.руб.)
Проведем интервальную оценку, т.е. найдем интервал, в котором с заданным уровнем вероятности находится средняя генеральной совокупности:
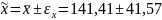или
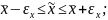
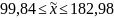(тыс.руб.)
Вывод: с доверительным уровнем вероятности 0,95 можно утверждать, что средняя цена за 1 сотку в период наблюдения находилась в пределах от
до
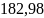тыс.руб.