Задача №207

Найти силу взаимодействия между тонкой бесконечной нитью с линейной плотностью заряда τ₁= 0,278 нКл/м и тонким стержнем длиной L = 17,1 см с линейной плотностью заряда τ₂= 0,4 нКл/м, если их оси взаимно перпендикулярны, а ближайший конец стержня, лежащего в радиальной плоскости, находится в 10 см от нити.

Дано: τ1= 0,278 нКл/м = 2,7810-10 Кл/м τ2= 0,4 нКл/м = 410-10 Кл/м L = 17,1 см = 0,171 м a = 10 см = 0,1 м	Решение
F – ?

Бесконечная, заряженная с линейной плотностью заряда τ₁, нить создает вокруг себя электрическое поле, обладающее осевой симметрией, напряженность которого на расстоянии r от нити рассчитывается по известной формуле:

Здесь ₀ = 8,8510^-12 Ф/м - диэлектрическая постоянная.

В торой заряд распределен вдоль стержня, поэтому для того, чтобы воспользоваться известной формулой силы, действующей на точечный заряд со стороны электрического поля, выделим на стержне, на расстоянии r от нити, бесконечно малый элемент стержня dr, который несет бесконечно малый заряд dq = τ₂ dr . Такой заряд можно считать точечным, поэтому силу его взаимодействия с заряженой нитью в вакууме можно записать в виде:

Тогда сила, действующая на весь стержень получается суммированием по всем его элементам:

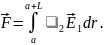
Очевидно, что все элементарные силы здесь имеют одинаковое направление, поэтому можно перейти от векторного сложения к алгебраическому сложению сил:

Подставим выражение для напряженности:

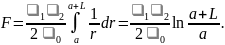
Подставим числа и произведем вычисления:

Ответ. F= 1,9910^-9 Н.

Задача №217

Заряд q = -510^-7 Кл равномерно распределен по всему объему однородного сферического диэлектрика ( = 3) радиусом R = 5,0 см.

Построить графики функций f1(r) и f2(r) для случаев:

1) г ⩽R; 2) г ⩾ R.

Вычислить разность потенциалов между точками r₁= 1 см и г₂= 8 см.

Дано:  = 3 R = 5,0 см = 0,05 м q = – 510-7 Кл r1= 1 см = 0,01м r2= 8 см = 0,08 м  = ( r1) – ( r2)	Решение
 – ? f1(r) – ? f2(r) – ?

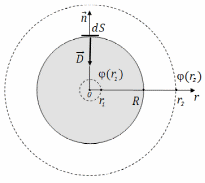
По теореме Остроградского-Гаусса поток вектора электрического смещения 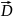через любую замкнутую поверхность равен заряду, заключенному внутри этой поверхности:

Здесь элемент площади 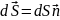имеет направление внешней нормали к замкнутой поверхности в данной точке, как указано на рисунке.

Для того, чтобы правильно выбрать поверхность интегрирования, необходимо знать, как направлен в каждой точке пространства. Для заряженной сферы, в силу симметрии, такое направление может быть только по радиусу, причем, так как поле создается отрицательным зарядом, то вектор направлен к центру сферы. Следовательно, поверхность интегрирования нужно выбирать в виде сферической поверхности радиуса r, центр которой совпадает с центром заряженного сферического диэлектрика.

Тогда, в силу симметрии, модуль вектора смещения на поверхности интегрирования имеет одинаковое значение, так как определяется на одинаковом расстоянии от центра, поэтому интеграл можно представить в виде:

Следует заметить, что модуль вектора – это существенно положительная величина. Иногда, когда заранее неизвестно направление вектора , после вычислений модуль получается отрицательным, что означает, что в действительности вектор направлен в противоположную сторону. В данной задаче, в связи с простым распределением зарядов, можно сразу указать реальное направление вектора и не прибегать к такой усложненной конструкции.

Выделим два случая.

1) г ⩽R

В этом случае внутри поверхности интегрирования содержится заряд:

где  – объемная плотность заряда диэлектрика, V –– объем внутри сферы интегрирования.

Объем внутри сферы интегрирования найдем па формуле объема шара:

Вычислим объемную плотность заряда диэлектрика объема V:

Таким образом, внутри поверхности интегрирования радиуса r находится заряд:

Здесь учтено, что заряд диэлектрика отрицательный.

Подставим полученные величины в теорему Остроградского-Гаусса:

Таким образом, внутри диэлектрика величина вектора смещения есть линейная функция радиуса.

Для изотропного диэлектрика:

Здесь ₀ = 8,8510^-12 Ф/м - электрическая постоянная,  – диэлектрическая проницаемость диэлектрика. Тогда

Чтобы построить графики полученных функций, подставим числовые значения.

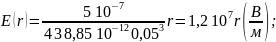
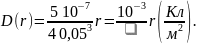
Чтобы отобразить вид полученных зависимостей на одном графике в сопоставимом масштабе, введем новые безразмерные функции по формулам:

Тогда

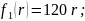
Расстояние r в эти функции необходимо подставлять измеренное в метрах.

Очевидно, что в заданной области графиками этих функций являются прямые линии разного наклона, выходящие из начала координат

2) г ⩾ R

В этом случае внутри поверхности интегрирования всегда содержится весь заряд:

Тогда теорема Остроградского-Гаусса примет вид:

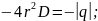
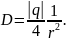
Учтем, что для вакуума = 1, поэтому в этом случае напряженность:

Чтобы построить графики полученных функций, подставим числовые значения.

Тогда безразмерные функции имеют вид:

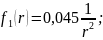
Построим по точкам графики функций и .

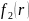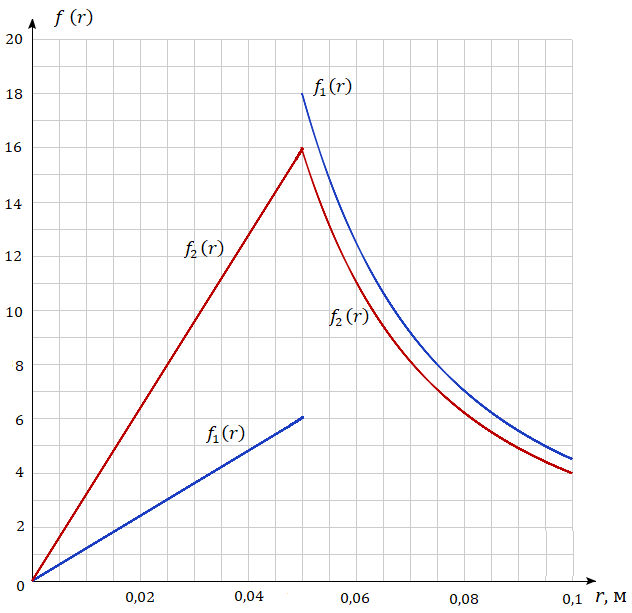
На графиках видно, что напряженность ( ) на границе диэлектрик-вакуум терпит разрыв, а электрическое смещение ( ) – меняется непрерывно.

Используя связь между потенциалом и напряженностью. найдем разность потенциалов между заданными точками:

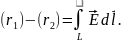
Здесь криволинейный интеграл берется по любой линии, соединяющей заданные точки. Выберем линию, совпадающую с радиусом, и учтем, что внутри диэлектрика и вне него напряженность имеет разную зависимость от радиуса:

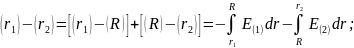
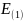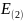Здесь и – модули функций напряженности для соответствующих зон, вычисленные выше.

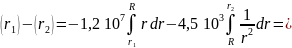
Подставим значения для радиусов:

Ответ. .