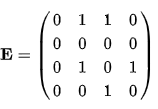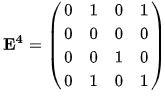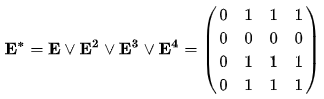9.3. Матрица смежности
Матрица смежности S - это квадратная матрица, в которой и число строк, и число столбцов равно n - числу вершин графа. В ячейки матрицы смежности записываются некоторые числа в зависимости от того, соединены соответствующие вершины рёбрами или нет, и от типа графа.
Матрица смежности для неориентированного графа
Элемент матрицы смежности sij неориентированного графа определяется следующим образом:
- равен единице, если вершины vi и vj смежны;
- равен нулю, если вершины vi и vj не смежны.
Если на диагонали матрицы стоят 1, то это показывает наличие петель.
Пример 5. Составить матрицу смежности для графа, представленного на рисунке ниже.
|
Пример 6. Или составить граф, или составить матрицу.
|
Таким образом, матрица смежности неориентированного графа симметрична относительно главной диагонали.
Матрица смежности для ориентированного графа
Элемент матрицы смежности sij ориентированного графа определяется следующим образом:
- равен единице, если из вершины vi в вершину vj входит дуга;
- равен нулю, если из вершины vi в вершину vj дуга не входит.
Если на диагонали матрицы стоят 1, то это показывает наличие петель.
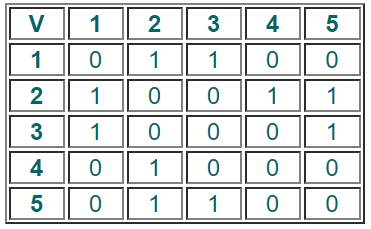
Пример 7. Составить матрицу смежности для графа, представленного на рисунке ниже.
|
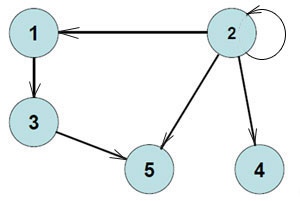
Пример 8. Составить матрицу смежности для графа, представленного на рисунке ниже. Или наоборот, построить граф по матрице смежности.
|
Таким образом, матрица смежности ориентированного графа не симметрична.
9.4. Список ребер
Пример 1.а. Составить список ребер для графа
|
9.1-9.4
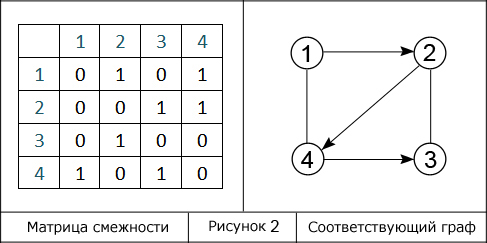
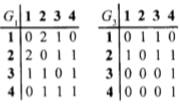
Пример 1. (москинова). Задать матрицами инцидентности и смежности, а также списком ребер графы G1 и G3. Матрицы инцидентности Матрицы смежности Список ребер графа G3
|
9.5. Матрица достижимости
Матрица достижимости простого ориентированного графа G=(V,E) — бинарная матрица замыкания по транзитивности отношения E (оно задаётся матрицей смежности графа). Таким образом, в матрице достижимости хранится информация о существовании путей между вершинами орграфа.
Возведение в степень матрицы смежности орграфа показывает, за сколько шагов (величина степени) можно достичь некой вершины.
Способы построения матрицы достижимости:
Перемножение матриц
Алгоритм Уоршелла
Связанные понятия
Пример 1. Перемножение матриц. (википедия) Дан простой связный ориентированный граф.
Матрица E1 показывает, в какие вершины мы можем попасть за 1 шаг. Матрица E2 показывает, в какие вершины мы можем попасть за 2 шага. Матрица E3 показывает, в какие вершины мы можем попасть за 3 шага. Матрица E4 показывает, в какие вершины мы можем попасть за 4 шага. Если посмотреть, то за второй шаг мы попадаем во все вершины, в которые не попали за первый шаг. Получим матрицу достижимости. Она показывает, есть ли путь из вершины a в вершину b.
Если просто взять и сложить найденные четыре матрица Е, Е2, Е3, Е4, то получим матрицу, которая показывает количество путей длины от 1 до 4 между вершинами орграфа.
|
|||
Пример 2.(мой). Составить матрицу достижимости и контрдостижимости.
|
