ПЗ 9. Графы.

Матрица смежности и инцидентности для неорграфа и орграфа. Матрица достижимости и контрдостижимости. Возведение в степень матрицы смежности орграфа. Маршрут, цепь, простая цепь, цикл, простой цикл в графе. Операции над графами (пересечение, объединение, декартово произведение). Деревья, цикломатическое и коцикломатическое числа.

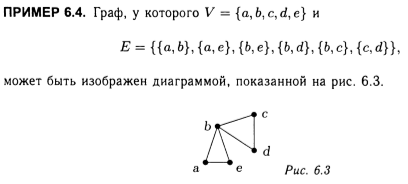
9.1. Графы

Граф — абстрактный математический объект, представляющий собой множество вершин графа и набор рёбер, то есть соединений между парами вершин.

Ребро – соединение двух вершин.

Концами ребра {a, b} называются вершины a, b.

Ребро {a, b} также называют инцидентным к вершинам a, b.

Смежные вершины – это вершины, инцидентны к одному ребру, т.е. которые являются концами одного ребра.

Ребра смежные, если они инцидентны к общей вершине.

Петля – ребро, которое соединяет вершину с самой собой. Если в графе допускается наличие петель, то он называется графом с петлями.

Мультиграф – граф, в котором допускается наличие более одного ребра между двумя вершинами.

Размеченный граф – каждая вершина графа отмечена.

Псевдограф – граф, в котором допускается наличие петель и существование более одного ребра между двумя вершинами.

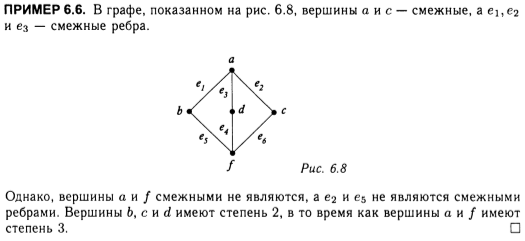
Пример 6.6. Указать смежные и несмежные вершины. Указать степень вершин.

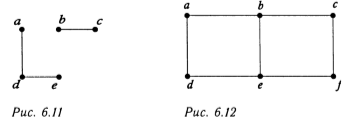
Пример. Подграфы.

Путь в графе — последовательность вершин, в которой каждая вершина соединена со следующей ребром.

Граф называется связным, если имеет путь между любыми двумя вершинами.

Ориентированный граф (кратко орграф) — (мульти) граф, рёбрам которого присвоено направление.

Граф, ни одному ребру которого не присвоено направление, называется неориентированным графом или неорграфом.

Степенью вершины v, обозначается deg(v), называется количество ребер, инцидентных этой вершине. Вершина степени 0 называется изолированной. В н-графе сумма степеней вершин всегда четна.

Граф В называется подграфом графа А, если каждая вершина и ребро графа В принадлежат графу А.

Для вершин орграфа определится две локальные степени:

1. p₁(v) – число ребер с начало в вершине v, или количество выходящих из v ребер;

2. p₂(v) – количество входящих в v ребер, для которых эта вершина является концом.

Петля дает вклад в обе эти степени.

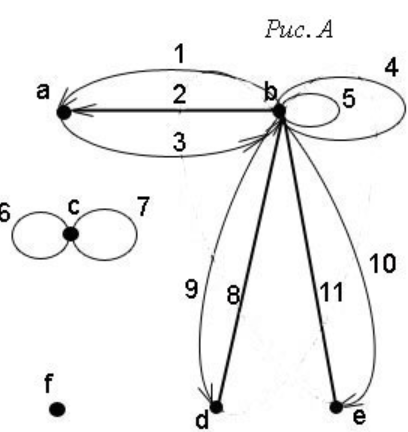
Пример 1.1. Задать аналитически граф, представленный на рисунке ниже. (рис. А)

Итак, задаём граф следующими множествами: множество вершин: V = {a, b, c, d, e, f} множество рёбер: U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11} множество инциденций: P = {(b, 1, a), (b, 2, a), (a, 3, b), (b, 4, b), (b, 5, b), (c, 6, c), (c, 7, c), (b, 8, d), (d, 8, b), (b, 9, d), (b, 10, e), (b, 11, e), (e, 11, b)}

Способы задания графом:

1. Матрица инцидентности;

2. Матрица смежности;

3. Списком ребер графа.

9.2. Матрица ицидентности

Матрица инцидентности — одна из форм представления графа, в которой указываются связи между инцидентными элементами графа (ребро(дуга) и вершина). Столбцы матрицы соответствуют ребрам, строки — вершинам.

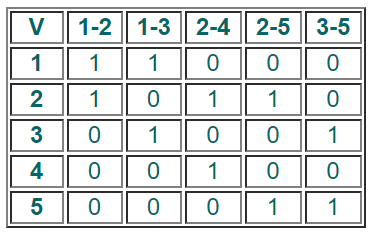
Матрица инцидентности для неорграфа

Если вершина инцидентна ребру, то ставим 1. Если вершина не инцидентна ребру, то в соответствующую ячейку ставим 0.

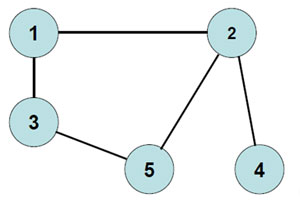
Пример 1. Составить матрицу инцидентности.

Пример 2. Составить матрицу инцидентности.

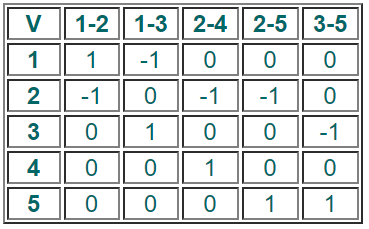
Матрица инцидентности для орграфа

Если вершина является началом ребра, то ставим 1. Если вершина является концом ребра, то ставим -1. Если не инцидентна ребру, то ставим 0. Если петля, то ставим любое другое число (например 2).

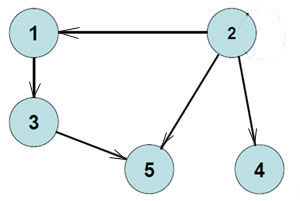
Пример 3. Составить матрицу инцидентности.

Пример 4. Построить граф.