Лабораторна по ЧМ 4
.docxЛабораторна робота №4
виконав студент групи АК-3-2ск
Козловський Євгеній
Варіант 14
Мета роботи: Опанувати методи простої ітерації, Зейделя, Ньютона
Знайти розв’язок системи нелінійних рівнянь
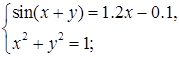
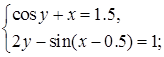
методами:
1. простої ітерації (а);
2. Зейделя (б);
3. Ньютона (б)
з точністю ε=10-3.
Відокремлення розв'язків
Відокремлення
розв'язків виконаємо графічним методом.
Для цього на декартовій площині XOY
побудуємо графіки двох функцій 
і 
Знайдемо
точку (або точки) перетину цих графіків і
спроектуємо її на вісь OX та на вісь OY.
Ці проекції точки перетину (позначимо
їх через 
та 
)
і дадуть початкове наближення до точного
розв'язку системи.
Рисунок 1.1 – Графіки неявних функцій f1(x, y) = 0 i f2(x, y) = 0
Спроектувавши точку перетину цих графіків в другій чверті на вісь OX, наближено одержимо x0 = 0.5; проекція цієї ж точки на вісь OY дає наступне наближене значення y0 = 0.55.
Отже, маємо початкове наближення
x0 = 0.5 y0 = 0.55
Використовуючи блок розв'язку пакету MathCad, одержимо "точний" розв'язок системи нелінійних рівнянь.
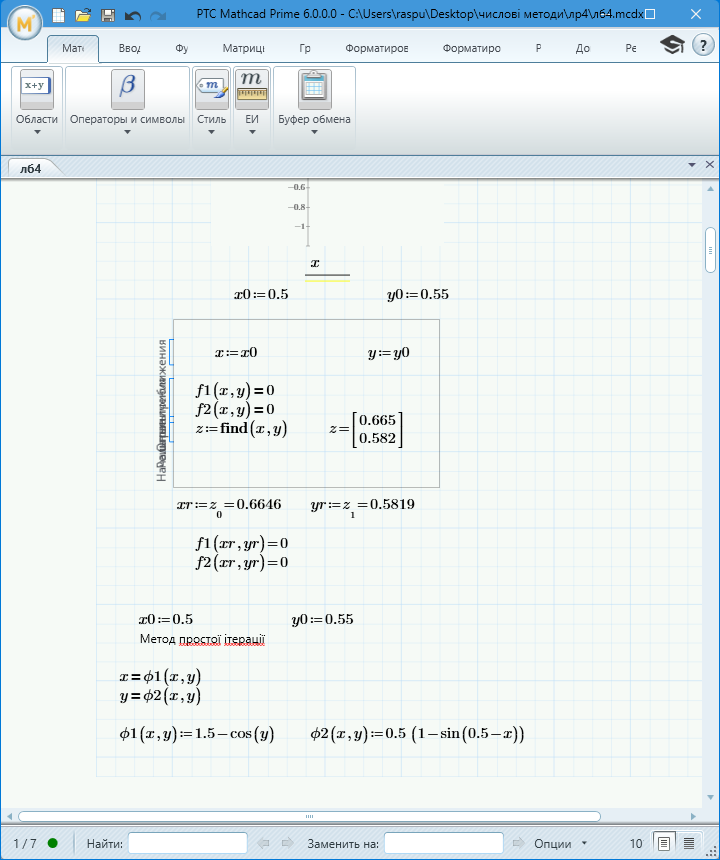
Рисунок 1.2 – Обчислення системи рівнянь за допомогою програмного забезпечення MathCad
Метод простої ітерації
Зведемо нашу систему до канонічної форми
x = φ1(x, y)
y = φ2(x, y)
де
φ1(x, y) = 1.5 – cos(y)
φ2(x, y) = 0.5 (1 – (0.5 – x))
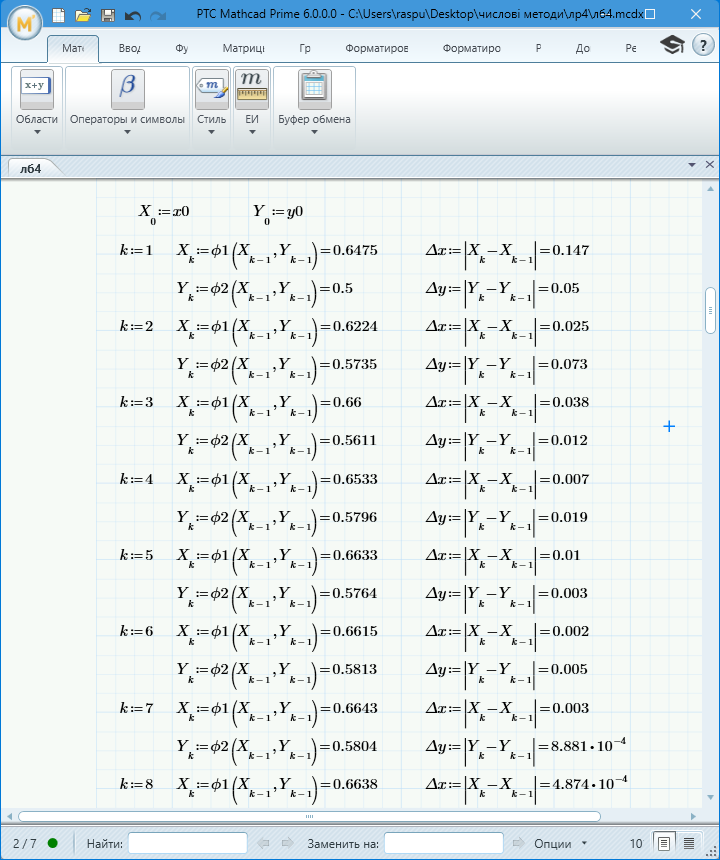
Рисунок 1.3 – Обчислення системи рівнянь методом простої ітерації за допомогою програмного забезпечення MathCad
Метод Зейделя
В
даному методі на кожній ітерації
необхідно розв'язати n
скалярних нелінійних рівнянь (n
- порядок системи),
-
початкова (стартова) точка (в загальному
випадку - вектор початкового наближення)
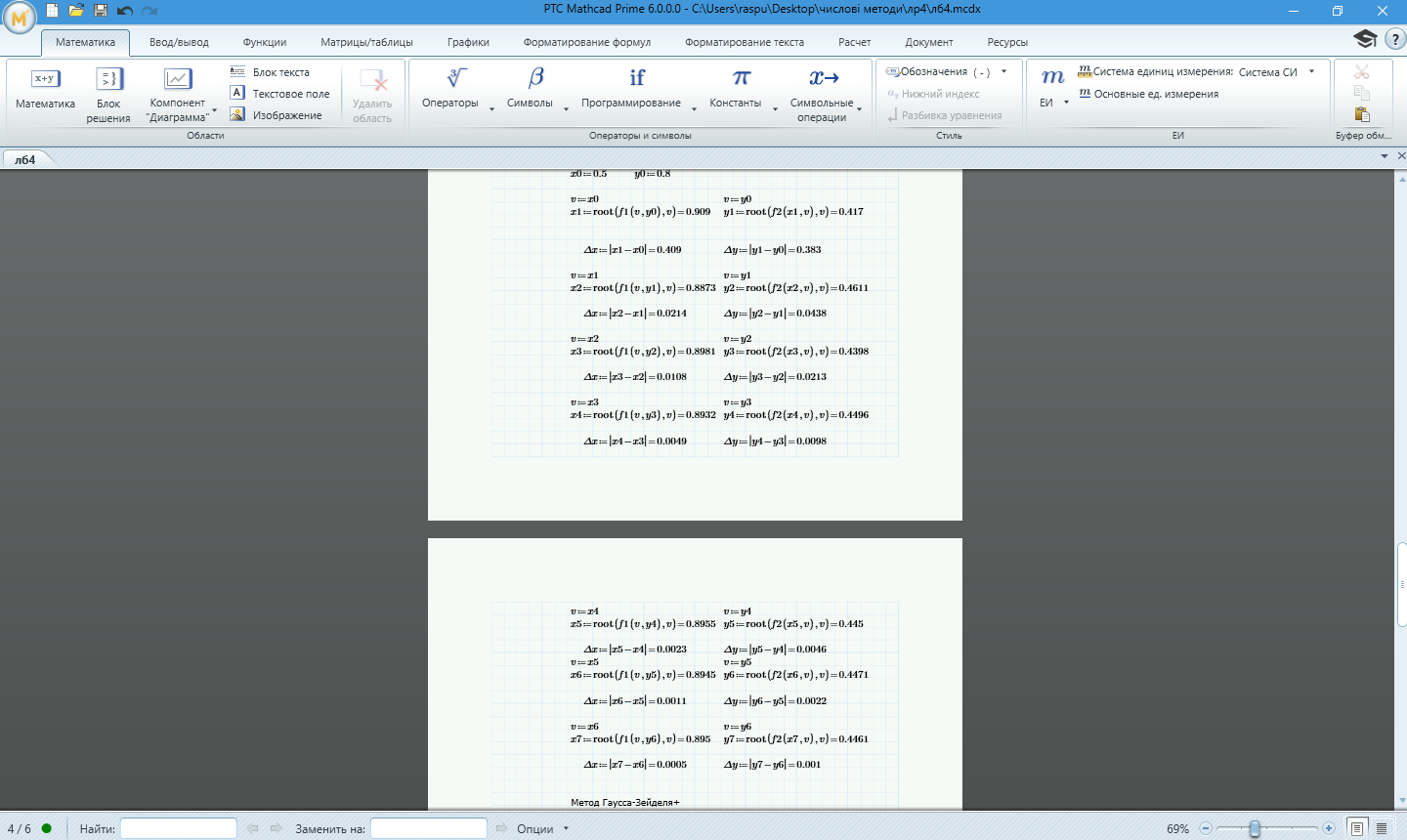Рисунок
1.4 – Обчислення методом Зейделя за
допомогою програмного забезпечення
MathCad
Метод Гаусса-Зейделя
Зведемо нашу систему до канонічної форми
x = φ1(x, y)
y = φ2(x, y)
де
φ1(x, y) = 1/1.2(sin(x + y) + 0.1)
φ2(x,
y)
=
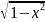
Тоді послідовні наближення за методом Гаусса-Зейделя набудуть вигляду
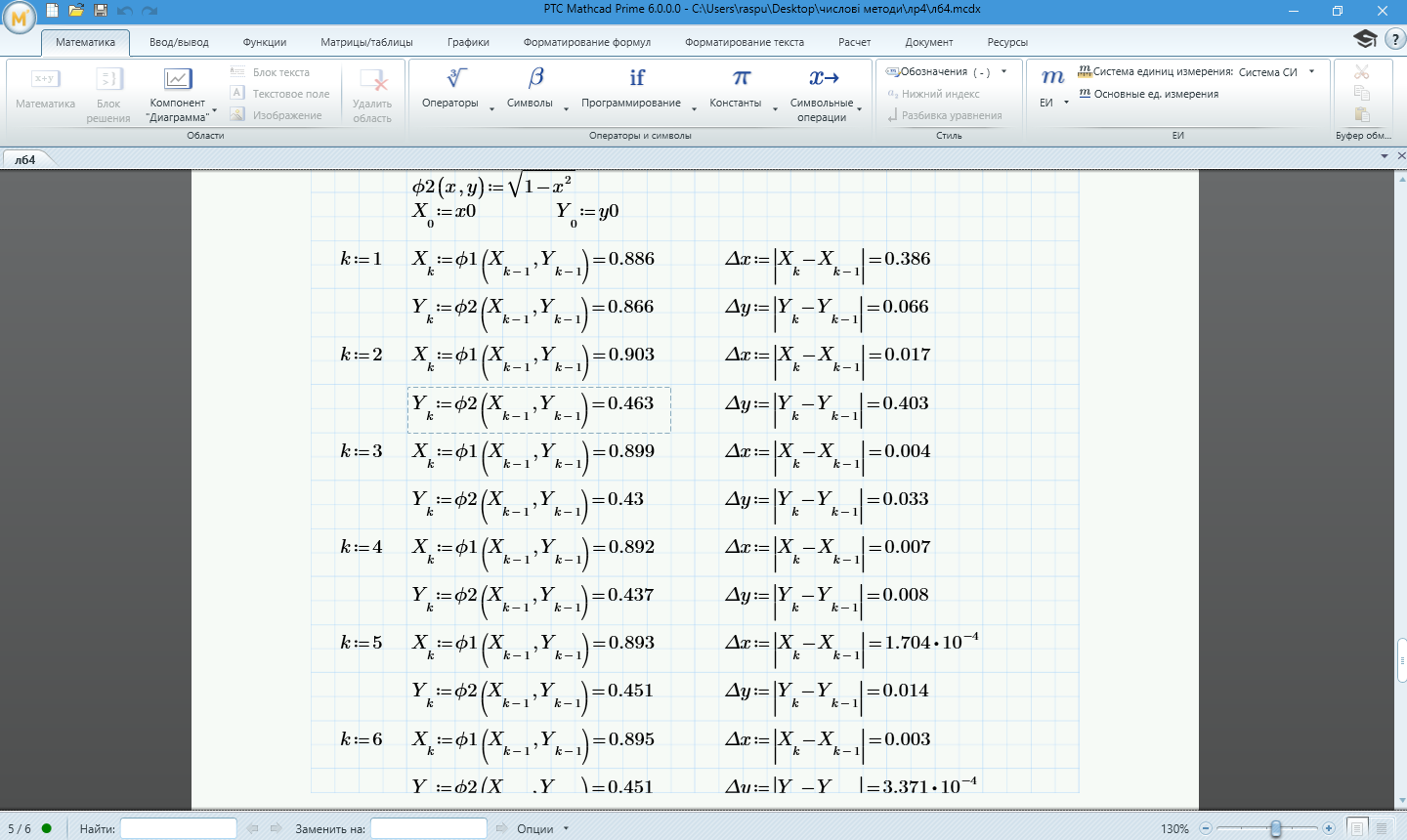
Рисунок 1.5 – Обчислення методом методом Гаусса-Зейделя за допомогою програмного забезпечення MathCad
Метод Ньютона
Знаходимо частинні похідні
Формуємо матричну функцію
і вектор-функцію
Задається вектор початкового наближення
Перша ітерація
Обчислюємо
матрицю
і
вектор
Розв'язуємо
СЛАР виду 
відносно 
Знаходимо
перше наближення до точного розв'язку
Після кожної ітерації необхідно перевіряти умову зупинки, аналогічну попереднім методам
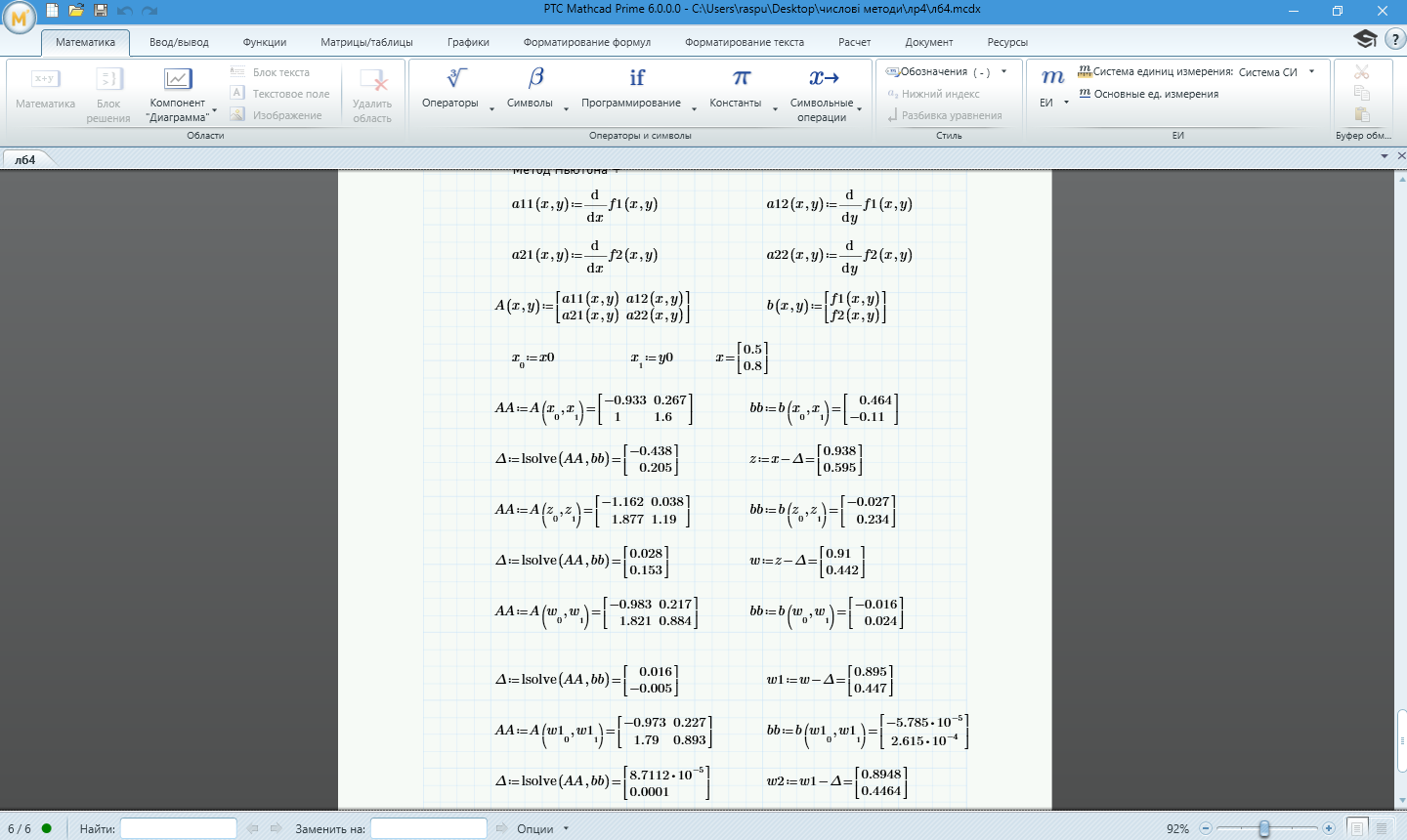
Рисунок 1.6 – Обчислення методом Ньютона за допомогою програмного забезпечення MathCad
Програми
Метод простої ітерації
#include <iostream>
#include <math.h>
using namespace std;
int main()
{ setlocale(LC_ALL, "Russian");
double x0,y0,x,y,d1,d2,eps;
cout << "Введите x0: " ;
cin>> x0;
cout << "Введите y0: ";
cin>> y0;
cout << "Введите точность е: ";
cin>> eps;
do
{
x=1.5-cos(y0);
y=0.5*(1-sin(0.5-x0));
d1=cos(y)+x-1.5;
d2=2*y-sin(x-0.5)-1;
x0=x;
y0=y;
}while(abs(d1)>eps && abs(d2)>eps);
cout<<"Результат: "<<"x="<<x<<" "<<"y="<<y<<endl;
return 0;}
Рисунок 1.7 – Результат виконання програми
Метод Ньютона
#include <math.h>
#include <conio.h>
#include <stdio.h>
#include <locale.h>
const int n = 2;
void GaussSolve (float a[n][n],float b[n],float x[n]);
float f1(float x[n]);
float f2(float x[n]);
float df1_dx(float x[n]);
float df1_dy(float x[n]);
float df2_dx(float x[n]);
float df2_dy(float x[n]);
float norm (float x[n]);
int main()
{setlocale (LC_ALL,"");
printf ("%s","Решение системы нелинейных уравнений\n");
int i, iter=0;
float eps = 0.001;
float a[n][n];
float b[n];
float x[n];
float xk[n],p[n];
xk[0]=1;xk[1]=1;
do{
iter++;
for (i=0;i<n;i++){
x[i] = xk[i];}
a[0][0]=df1_dx(x); a[0][1]=df1_dy(x);
a[1][0]=df2_dx(x); a[1][1]=df2_dy(x);
b[0]=-f1(x); b[1]=-f2(x);
GaussSolve (a,b,p);
for (i=0;i<n;i++){
xk[i] = x[i] + p[i];}}
while (fabs(norm (x) - norm(xk))>=eps);
printf ("%s","Вектор решения: [ ");
for (i=0;i<n;i++)
{printf ("%f ",xk[i]);}
printf ("%s","]\n");
printf ("Решение найдено за %i интераций\n",iter);
return 0;}
float f1(float x[n]){
return sin(x[0]+x[1])-1.2*x[0]+0.1;}
float f2(float x[n]){
return pow(x[0],2)+pow(x[1],2)-1;}
float df1_dx(float x[n]){
return cos(x[0]+x[1])-1.2;}
float df1_dy(float x[n]){
return cos(x[0]+x[1]);}
float df2_dx(float x[n]){
return 2*x[0];}
float df2_dy(float x[n]){
return 2*x[1];}
float norm (float x[n]){
float sum = 0;
for (int i=0;i<n;i++){
sum+=x[i]*x[i];}
return sqrtf(sum);}
void GaussSolve (float a[n][n],float b[n],float x[n]){
const float eps=0.001;
float tmpValue;
int i,j,k,z;
float dblLeadElement;
for(i=0; i<n; i++)
{dblLeadElement=a[i][i];
float tmpMax = dblLeadElement;
int tmpMaxNumber = i;
for (z=i;z<n;z++){
if (a[z][i]>tmpMax){tmpMax = a[z][i];tmpMaxNumber=z;}}
for (z=i;z<n;z++){
tmpValue = a[i][z];
a[i][z] = a[tmpMaxNumber][z];
a[tmpMaxNumber][z] = tmpValue;
}tmpValue = b[i];
b[i] = b[tmpMaxNumber];
b[tmpMaxNumber] = tmpValue;
dblLeadElement = tmpMax;
for(j=i; j<n; j++){
a[i][j]/=dblLeadElement;}
b[i]/=dblLeadElement;
for(k=i+1; k<n; k++)
{float dblToDivide=a[k][i]/a[i][i];
for(z=i;z<n; z++){
a[k][z]-=a[i][z]*dblToDivide;}
b[k]-=b[i]*dblToDivide;}}
x[n-1]=b[n-1];
for(k=n-2; k>=0; k--){
float sum=b[k];
for(j=k+1; j<n; j++){
sum-=a[k][j]*x[j];}
x[k]=sum;}}
Рисунок 1.7 – Результат виконання програми
Висновок: на даній лабораторній роботі було обчислено системи нелійних рівнянь за допомогою методів простої ітерації, Зейделя, Ньютона.