Лабораторна по ЧМ 2

Лабораторна робота №2

виконав студент групи АК-3-2ск

Козловський Євгеній

Варіант 14

Мета роботи: Опанувати методи прямокутників, трапецій, Сімпсона та порівняти їх точність

Знайти наближене значення визначеного інтегралу

Методами:

1. прямокутників (лівих, правих, середніх);

2. трапеції;

3. Сімпсона (метод парабол).

Для оцінки точності наближених методів обчислимо точне значення інтеграла S=0.305

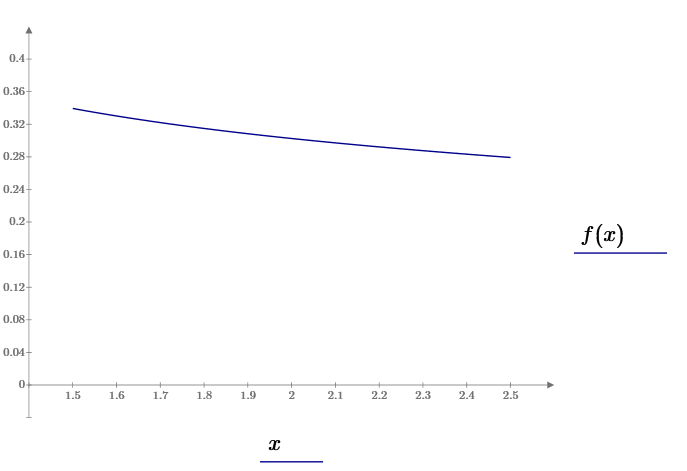
Рисунок 1.1 – Графік підінтегральної функції f(x)

Задамо n - кількість елементарних відрізків, на які розбивається відрізок [a,b], n=8. Обчислимо h - крок інтегрування h=0.125. Знайдемо xi - координати точок розбиття відрізка [a,b]. Обчислимо yi - значення підінтегральної функції f(x) в точках xi.

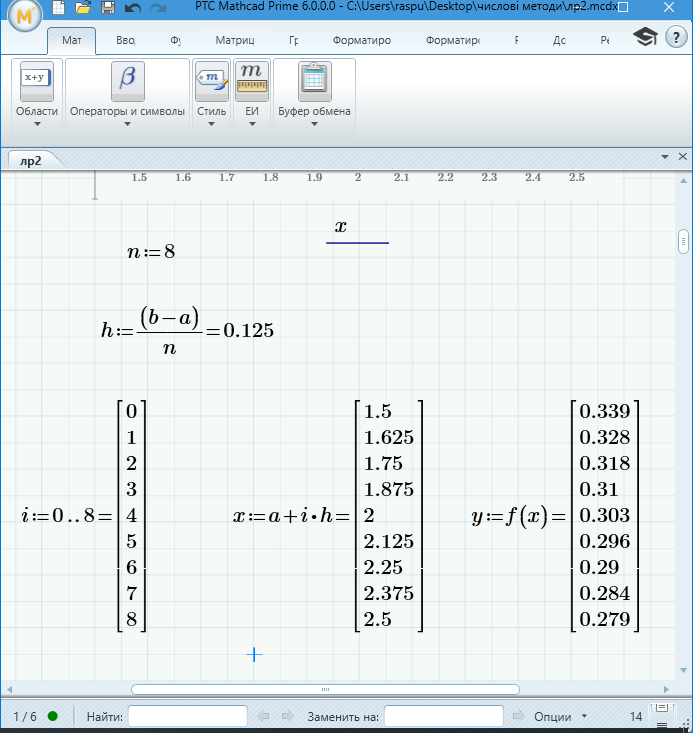
Рисунок 1.2 – Обчислення h, xi, yi за допомогою програмного забезпечення MathCad

Методи прямокутників

Цей метод безпосередньо використовує заміну визначеного інтеграла інтегральною сумою. В якості точок x _{i ­} можуть вибиратися ліві (x _i = x _i-1) чи праві (x _i = x_i) кордону елементарних відрізків. Позначаючи f (x _i) = y _i і D x _i = h _i, можна отримати наступні формули методу прямокутників.

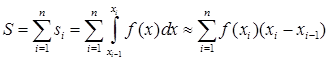
Широко поширеним і більш точним є вид формули прямокутників, що використовує значення функції в середніх точках елементарних відрізків (в напівцілим вузлах):

Цей алгоритм зазвичай називають методом середніх.

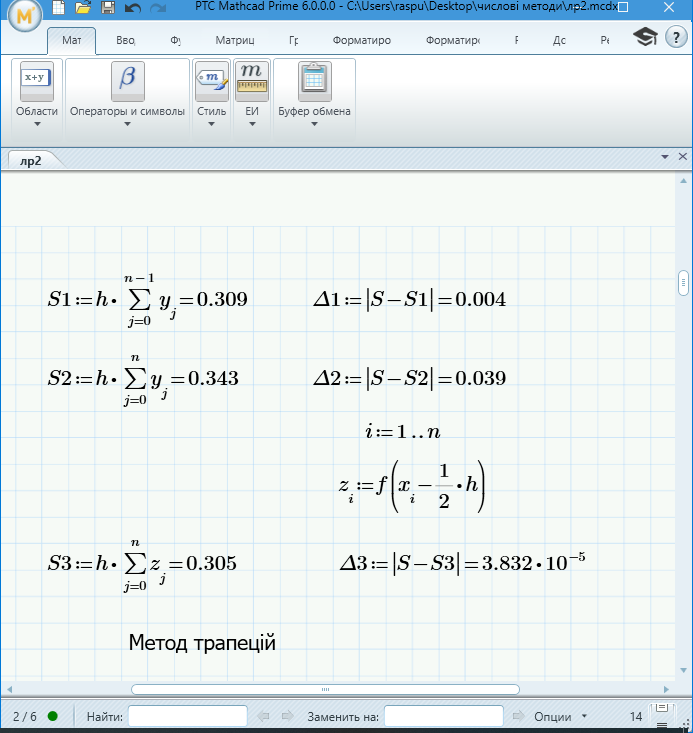Рисунок 1.3 – Обчислення методом прямокутників за допомогою програмного забезпечення MathCad

S1 - наближене значення інтеграла, обчислене за методом лівих прямокутників, S2 - наближене значення інтеграла, обчислене за методом правих прямокутників, S3 - наближене значення інтеграла, обчислене за методом середніх прямокутників, ∆1-3 – обчислення абсолютної похибки.

Метод трапецій

Метод трапецій можна одержати, якщо підінтегральну функцію f(x) на інтервалі [x_i-1, x_i] замінити поліномом першої степені, тобто даний метод використовує локальну лінійну інтерполяцію підінтегральної функції. З геометричної точки зору це означає, що графік функції y=f(x) заміняється ламаною, що сполучає точки (x_i, y_i), y_i=f(x_i) відрізками прямих.

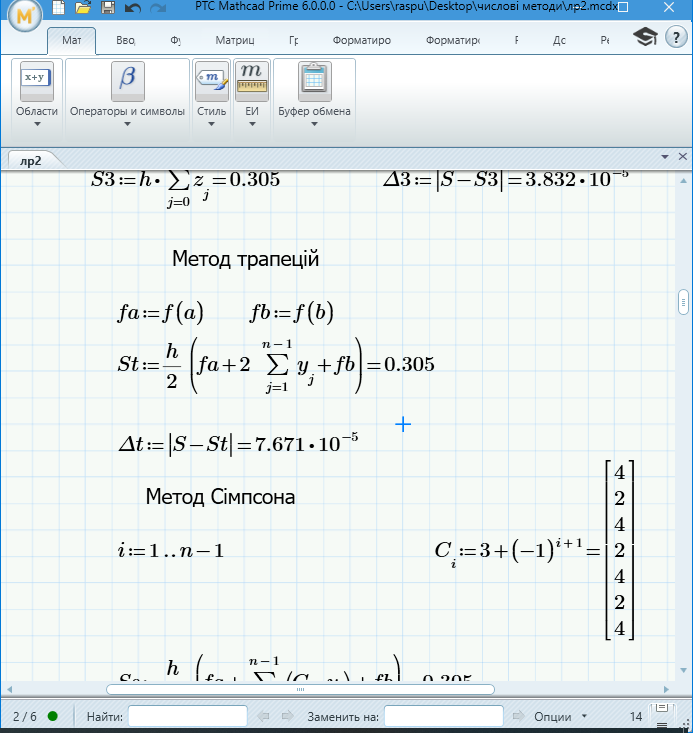
Рисунок 1.4 – Обчислення методом прямокутників за допомогою програмного забезпечення MathCad

St - наближене значення інтеграла, обчислене за методом трапецій, ∆t - абсолютна похибка формули трапецій.

Метод Сімпсона (парабол)

Рисунок 1.5 – Обчислення методом Сімпсона за допомогою програмного забезпечення MathCad

Ss - наближене значення інтеграла, обчислене за методом Сімпсона,

С - допоміжний вектор коефіцієнтів, ∆і - абсолютна похибка формули Сімпсона.

Порівняльний аналіз результатів та абсолютних похибок методів

Рисунок 1.6 – Порівняльний аналіз результатів та абсолютних похибок методів

S - Наближені значення інтегралів, ∆ - абсолютні похибки

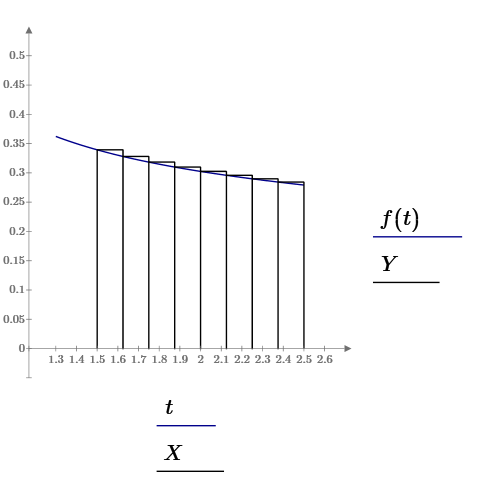
Рисунок 1.7 – Графічна ілюстрація методу лівих прямокутників

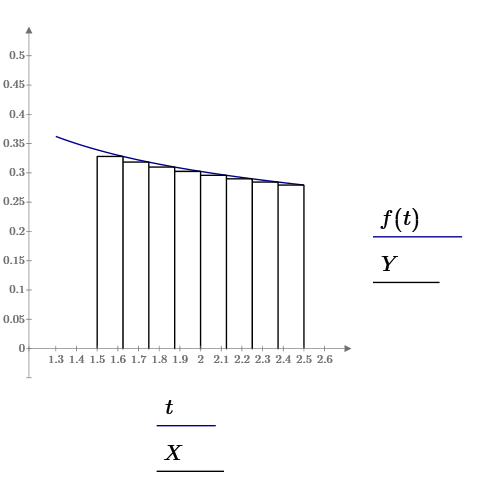
Рисунок 1.8 – Графічна ілюстрація методу правих прямокутників

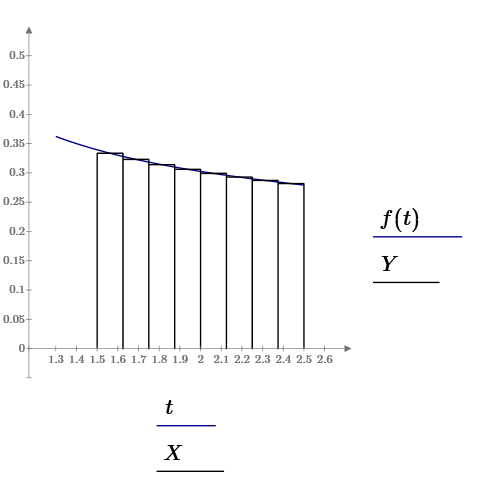
Рисунок 1.9 – Графічна ілюстрація методу середніх прямокутників

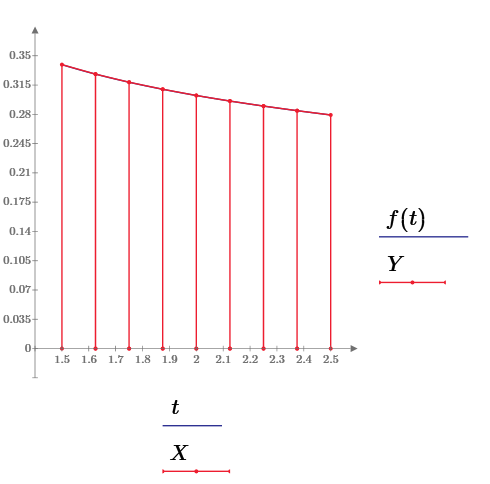
Рисунок 1.10 – Графічна ілюстрація методу середніх трапецій

Правило Рунге обчислення визначеного інтегралу з заданою точністю

Нехай ε = 10^-3

Виберемо один з вище розглянутих методів, наприклад, метод лівих прямокутників і для зручності введемо функцію F(m, a, b), яка обчислює наближене значення інтегралу методом лівих прямокутників.

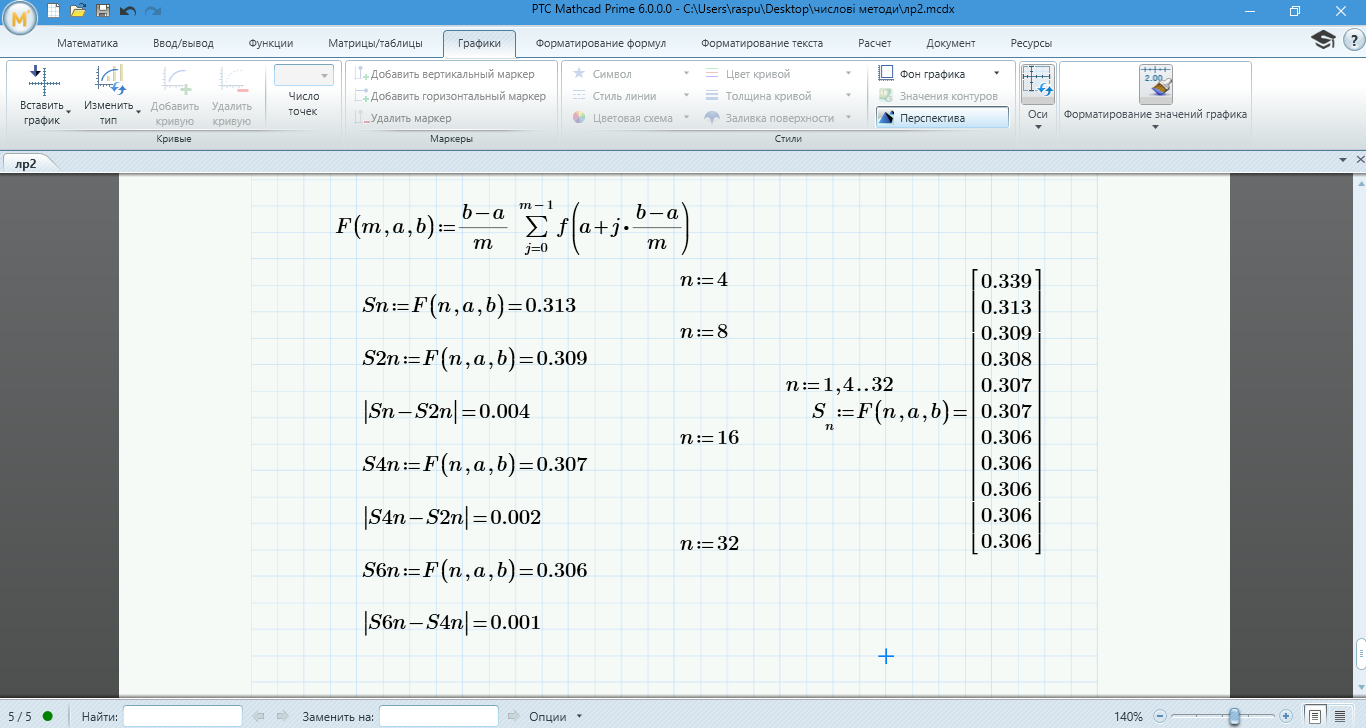
Рисунок 1.11 – Обчислення визначеного інтегралу з заданою точністю ε правилом Рунге за допомогою програмного забезпечення MathCad

Програма обчислення визначеного інтегралу

#include <iostream>

#include <math.h>

#include <stdio.h>

using namespace std;

double f(double x)

{ return (log10(pow(x,2)+4)/(sqrt(sin(x)+2*pow(x,2))));

}

int main()

{ setlocale (LC_ALL, "Russian") ;

int i; // счётчик

double Integral,a ,b,n,h; ; // здесь будет интеграл

do{

cout <<"Введите а = ";

cin>>a;

cout <<"Введите b = ";

cin>>b;

cout <<"Введите n = ";

cin>>n;

}while(a >= b);

h = (b - a) / n;

Integral = 0.0;

for(i = 0; i <= n-1; i++)

Integral = Integral + h * f(a + h * i );

double i1=Integral;

Integral = 0.0;

for(i = 1; i <= n+1; i++)

Integral = Integral + h * f(a + h * i );

double i2=Integral;

Integral = 0.0;

for(i = 1; i <= n; i++)

Integral = Integral + h * f(a + h * (i - 0.5));

double i3=Integral;

Integral = h * (f(a) + f(b)) / 2.0;

for(i = 1; i <= n-1; i++)

Integral = Integral + h * f(a + h * i);

double i4=Integral;

Integral = h * (f(a) + f(b)) / 6.0;

for(i = 1; i <= n; i++)

Integral = Integral + 4.0 / 6.0 * h * f(a + h * (i - 0.5));

for(i = 1; i <= n-1; i++)

Integral = Integral + 2.0 / 6.0 * h * f(a + h * i);

double i5=Integral;

cout <<"Результат левых прямоугольников: " << i1;

cout <<" Погрешность: " << i5-i1 << "\n";

cout <<"Результат правых прямоугольников: "<< i2;

cout <<" Погрешность: " << fabs(i5-i2) << "\n";

cout <<"Результат средних прямоугольников: " << i3;

cout <<" Погрешность: " << i5-i3 << "\n";

cout <<"Результат по формуле трапеций: " << i4;

cout <<" Погрешность: " << i5-i4 << "\n";

cout <<"Результат по формуле Симпсона: " << i5;

cout <<" Погрешность: " << i5-i5 << "\n";

system("pause");

}

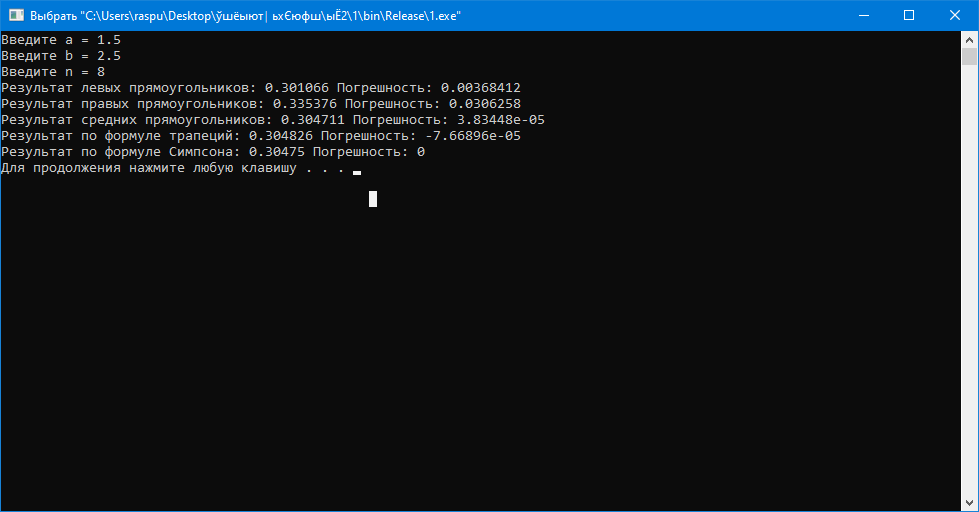
Рисунок 1.12 – Результат виконання програми

Висновок: на даній лабораторній роботі було обчислено визначені інтеграли за допомогою методів:

1. методу лівих прямокутників, наближене значення інтеграла дорівнювало S1=0.309, а абсолютна похибка Δ1=0.004;

2. методу правих прямокутників, наближене значення інтеграла дорівнювало S2=0.343, а абсолютна похибка Δ2=0.039;

3. методу середніх прямокутників, наближене значення інтеграла дорівнювало S1=0.305, а абсолютна похибка Δ3=3.832*10^-5;

4. методу трапецій, наближене значення інтеграла дорівнювало St=0.305, а абсолютна похибка Δt=7.671*10^-5;

5. методу Сімпсона, наближене значення інтеграла дорівнювало Ss=0.305, а абсолютна похибка Δs=3.486*10^-7.

Найменшу похибку дав метод Сімпсона, а отже він і є найточнішим.