
невизначений інтеграл 1 роду
.pdfЛекція 8. Криволінійний інтеграл першого роду
Короткий зміст Розділ 8.1. Поняття криволінійного інтеграла пер-
шого роду (за довжиною дуги)
8.1.1.Означення криволінійного інтеграла першого
роду
8.1.2.Фізичний та геометричний зміст криволінійного інтеграла першого роду
8.1.3.Умови існування криволінійного інтеграла першого роду
8.1.4Властивості криволінійного інтеграла першого роду
Розділ 8.2. Обчислення криволінійного інтеграла першого роду
8.2.1.Обчислення криволінійного інтеграла першого роду для плоских кривих
8.2.2.Криволінійний інтеграл першого роду для просторових кривих
Короткий зміст
Уцій лекції:
—розглянуто криволінійний інтеграл першого роду — узагальнення поняття визначеного інтеграла на випадок, коли областю інтегрування є деяка крива, наведено геометричний та фізичний зміст криволінійного інтеграла першого роду і його властивості;
—наведено формули обчислення криволінійного інтеграла першого роду для різних способів задання кривої на площині і в просторі.
2 |
Лекція 8. Криволінійний інтеграл першого роду |
8.1. Поняття криволінійного інтеграла першого роду (за довжиною дуги)
8.1.1. Означення криволінійного інтеграла першого роду
Узагальнимо поняття визначеного інтеграла на випадок, коли областю інтегрування є деяка крива.
Означення 8.1. |
|
Криву AB , що задана параметричними рівняннями |
|
|||||
|
|
x |
x(t), |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t , |
|
||
|
|
|
|
y(t), |
|
|||
|
|
y |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
називають гладкою, якщо функції x(t), y(t), x (t), y (t) |
||||||
|
|
неперервні на відрізку ; , причому |
|
|||||
|
|
|
2 |
|
|
2 |
0, t ; . |
|
|
|
x (t) |
|
y (t) |
|
|
||
|
|
Якщо для скінченної кількості точок похідні не існу- |
||||||
|
|
ють, або одночасно дорівнюють нулю, то криву нази- |
||||||
|
|
вають кусково-гладкою. |
|
|
|
|||
Нехай на площині |
Oxy задана гладка або кусково-гладка крива AB , в точ- |
|||||||
ках якої визначена неперервна функція f (x, y) (рис. 8.1). |
|
|||||||
y
|
|
|
|
|
Mi |
A An 1 |
|
|
|
|
|
|
|
|
|
|
|
i |
B An |
|
|
|
|||
|
|
|
|
|
Ai 1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 |
|
|
|
|
|
|
|
|
|
|
|
|
A A0 |
|
|
x |
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 8.1 |
|
|
|
|
|
|
|
|
Довільно розіб’ємо криву точками A A0, A1, ..., An 1, An B на n еле- |
|||||||||||
ментарних дуг, на |
кожній дузі Ai 1Ai виберемо довільну |
точку Mi( i; i ), |
||||||||||
i |
|
, і складемо суму |
|
|
|
|
|
|
|
|||
1, n |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
n f( i, i ) li , |
|
|
(8.1) |
||||
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
де li |
— довжина дуги Ai 1Ai . Суму (8.1) називають інтегральною сумою для |
|||||||||||
функції |
f (x, y) за довжиною дуги кривої. Нехай max li — найбільша з |
|||||||||||
|
|
|
|
|
|
|
|
|
|
1 i n |
|
|
довжин елементарних дуг Ai 1Ai . |
|
|
|
|
|
|
|
|||||
Означення 8.2. |
|
|
Якщо існує скінченна |
|
n |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
f( i, i ) li , |
|
|
||
|
|
|
|
|
|
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
яка не залежить ні від способу розбиття кривої AB на |
|||||||
|
|
|
|
|
елементарні |
дуги, |
|
|
ні |
від |
вибору |
точок |
|
|
|
|
|
Mi( i ; i ) Ai 1Ai , то цю границю називають криволі- |
|||||||
|
|
|
|
|
нійним інтегралом першого |
роду (або криволінійним |
||||||
Лекція 8. Криволінійний інтеграл першого роду |
3 |
||||||
|
|
|
|
|
|
||
|
|
інтегралом за довжиною дуги) від функції |
f (x, y) |
||||
|
|
||||||
|
|
вздовж кривої AB і позначають f(x, y)dl . |
|
|
|||
Таким чином, |
|
|
|
|
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
def |
n |
|
|
|
|
|
|
f( i, i ) li. |
|
(8.2) |
||
|
|
f(x, y)dl lim |
|
||||
|
|
AB |
0 i 1 |
|
|
|
|
В разі існування границі (8.2) функцію f (x, y) називають інтегровною на кривій AB , криву AB називають контуром інтегрування, A — початковою, B — кінцевою точками інтегрування.
8.1.2. Фізичний та геометричний зміст криволінійного інтеграла першого роду
З’ясуємо фізичний зміст криволінійного інтеграла першого роду. Якщо вздовж
неоднорідної матеріальної кривої AB розподілено масу з лінійною густиною
(x, y), то
|
n |
|
m lim |
( i, i ) li (x, y)dl, |
|
0 i 1 |
AB |
|
тобто з фізичної точки зору криволінійний інтеграл першого роду від невід’ємної функції вздовж деякої кривої дорівнює масі цієї кривої.
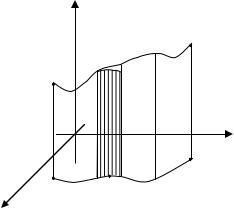
Розглянемо геометричний зміст криволінійного інтеграла першого роду. Нехай на площині Oxy задана деяка крива AB , на якій визначена неперервна функція f (x, y) 0. Розглянемо циліндричну поверхню, твірні якої мають довжину f (x, y) і паралельні осі Oz , а напрямна збігається з кривою AB Oxy
(рис. 8.2).
y
z f (x, y)
|
O |
x |
|
B |
|
|
|
|
A |
|
B |
|
|
z
Рис. 8.2
Тоді площа зображеної циліндричної поверхні дорівнює
|
n |
|
S lim |
f( i, i ) li f (x, y)dl. |
|
0 i 1 |
AB |
|

4 Лекція 8. Криволінійний інтеграл першого роду
8.1.3. Умови існування криволінійного інтеграла першого роду
Візьмемо на кривій AB за параметр довжину дуги l , що відраховується від по-
чаткової точки A. Тоді криву AB задають рівняння |
|
||
x x(l), |
|
|
|
|
|
|
|
|
, |
(8.3) |
|
|
0 l l |
||
y y(l), |
|
|
|
|
|
|
|
|
|
|
|
де l — довжина кривої AB . |
|
|
|
Рівняння (8.3) називають натуральними рівняннями кривої AB . Функція f (x, y), що задана на кривій, при переході до натуральних рівнянь стане функ-
цією змінної l : f (x l , y l ). Позначимо через li |
(i 1, 2, ..., n) значення пара- |
метра l , що відповідає точці Mi , тоді інтегральна сума (8.1) набуде вигляду |
|
n |
|
f(x(li ), y(li )) li. |
(8.4) |
i 1
Бачимо, що (8.4) — це інтегральна сума для визначеного інтеграла
l
f x(l), y(l) dl.
0
Оскільки інтегральні суми (8.1) та (8.4) рівні, то рівні між собою і інтеграли, що їм відповідають. Тобто
|
|
|
l |
|
|
|
f(x, y)dl |
f x(l), y(l) dl. |
(8.5) |
|
|
AB |
0 |
|
Таким чином, криволінійний інтеграл (8.2) існує за умов існування визначе- |
||||
ного інтеграла в правій частині рівності (8.5). Сформулюємо теорему. |
|
|||
Теорема 8.1. |
|
Якщо функція f (x, y) неперервна вздовж гладкої кривої |
||
|
|
AB , то існує криволінійний інтеграл |
|
|
|
|
|
f(x, y)dl . |
|
|
|
|
AB |
|
8.1.4. Властивості криволінійного інтеграла першого роду
З формули (8.5) випливає, що властивості криволінійного інтеграла першого роду аналогічні властивостям визначеного інтеграла. Сформулюємо основні з них.
Властив0сті |
1) (Нормованість). 1 dl |
dl l , |
|
||
|
AB |
AB |
|
де l — довжина дуги кривої AB . |
|
|
2) (Незалежність від напрямку кривої інтегрування). |
|
|
Криволінійний інтеграл першого роду не залежить від |
|
|
напрямку шляху інтегрування, тобто |
|
f(x, y)dl f(x, y)dl .
AB |
BA |
3) (Лінійність). Якщо для кожної з функцій f (x, y) і g(x, y) існує криволінійний інтеграл вздовж кривої AB ,
|
Лекція 8. Криволінійний інтеграл першого роду |
5 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
то для функції f (x, y) g(x, y), де , — довільні |
|||||||||||||||
|
|
|
||||||||||||||||
|
|
|
сталі, також існує криволінійний інтеграл по кривій |
|||||||||||||||
|
|
|
AB , причому |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
f (x, y) g(x, y) dl f (x, y)dl g(x, y)dl. |
|||||||||||||||
|
|
|
AB |
|
|
|
AB |
AB |
||||||||||
|
|
|
4) |
(Адитивність). Якщо крива AB AC CB і для |
||||||||||||||
|
|
|
f (x, y) існує криволінійний інтеграл по AB , то існують |
|||||||||||||||
|
|
|
інтеграли f(x, y)dl , f(x, y)dl , причому |
|
|
|||||||||||||
|
|
|
|
|
AC |
CB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(x, y)dl f(x, y)dl f (x, y)dl . |
|||||||||||||
|
|
|
|
|
AB |
AC |
|
|
|
|
CB |
|
|
|||||
|
|
|
5) (Збереження знаку). Якщо f (x, y) 0 на кривій AB , |
|||||||||||||||
|
|
|
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(x, y)dl 0 . |
|
|
|||||||||
|
|
|
|
|
|
|
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6) (Оцінка модуля інтеграла). Якщо функція f (x, y) інте- |
|||||||||||||||
|
|
|
гровна на кривій |
AB , то функція |
|
f (x, y) |
|
|
також інтег- |
|||||||||
|
|
|
|
|
||||||||||||||
|
|
|
ровна на AB і справедлива нерівність |
|
|
|||||||||||||
|
|
|
|
|
|
f(x, y)dl |
|
|
f (x, y) |
|
dl . |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
AB |
|
AB |
|
|
||||||||
|
|
|
7) |
(Теорема про середнє). Якщо функція f (x, y) непере- |
||||||||||||||
|
|
|
рвна на кривій |
AB , то |
на цій кривій |
існує точка |
||||||||||||
|
|
|
( ; ) AB така, що |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
f(x, y)dl f ( , ) l |
|
|
|||||||||
|
|
|
|
|
|
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де l — довжина дуги кривої AB . |
|
|
|||||||||||||
|
|
|
|
Властивість 2 означає, що межі інтегрування в криво- |
||||||||||||||
|
Зауваження 8.1. |
|
|
|||||||||||||||
|
|
|
|
лінійному інтегралі першого роду завжди треба брати |
||||||||||||||
|
|
|
|
від меншого до більшого значення змінної, оскільки за |
||||||||||||||
|
|
|
|
означенням li |
— довжина дуги, тому li |
0 . |
||||||||||||
|
|
|
|
У визначеному інтегралі величина xi може бути як |
||||||||||||||
|
|
|
|
додатною, так і від’ємною. У зв’язку з чим |
|
|
||||||||||||
|
|
|
|
|
|
|
b |
a |
|
|
||||||||
|
|
|
|
|
|
|
f(x)dx f(x)dx. |
|
|
|||||||||
|
|
|
|
|
|
|
a |
b |
|
|
||||||||

6 |
Лекція 8. Криволінійний інтеграл першого роду |
8.2. Обчислення криволінійного інтеграла першого роду
8.2.1. Обчислення криволінійного інтеграла першого роду для плоских кривих
Формула (8.5), яка зводить криволінійний інтеграл до звичайного, не є зручною для обчислення, бо не завжди можна легко знайти натуральні рівняння кривої (8.3). Тому наведемо формули обчислення криволінійних інтегралів першого роду
для різних способів задання кривої. |
|
|
1. Нехай крива AB задана параметричними рівняннями |
||
x |
x(t), |
|
|
|
|
|
|
t , |
|
y(t), |
|
y |
|
|
|
|
|
|
|
|
причому точці A відповідає значення t |
, а точці B — t |
. Припустимо, |
||||||||||||||||||||
що функції x(t) та y(t) неперервні на відрізку ; |
разом зі своїми похідними |
|||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
2 |
0, t |
|
; |
|
. |
||||||
x (t) та y (t) і виконується нерівність x (t) |
|
y (t) |
|
|
|
|
||||||||||||||||
|
Тоді диференціал дуги кривої обчислюється за формулою |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dl |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
(8.6) |
|
|
|
|
(x (t)) |
(y (t)) dt, |
|
|
|
|
|
|
|
|
|
||||||||
а криволінійний інтеграл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(x, y)dl f(x(t), y(t)) |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
(8.7) |
||||||
|
|
|
|
(x (t)) |
(y (t)) dt. |
|
|
|
|
|||||||||||||
|
|
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рівнянням |
||||
|
2. Якщо крива AB в декартових координатах задана явним |
|||||||||||||||||||||
|
|
|
|
y y(x), a x b, |
|
|
|
|
|
|
|
|
|
|
|
|||||||
причому функція y(x) |
неперервно диференційовна на a;b |
і точці A відпові- |
||||||||||||||||||||
дає значення x a , а |
точці B — x b , то, обираючи змінну x |
за параметр, |
||||||||||||||||||||
одержуємо формулу для обчислення криволінійного інтеграла першого роду для явно заданої кривої
|
b |
|
|
|
|
|
f(x, y)dl f(x, y(x)) |
|
2 |
|
(8.8) |
1 (y (x)) dx. |
|||||
AB |
a |
|
|
|
|
3.Розглянемо криву AB , яка задається рівнянням в полярних координатах
( ), 1 2 ,
функція ( ) неперервна на 1; 2 |
|
|
і має неперервну похідну ( ), значення |
||
1 відповідає точці A, а значення |
2 — точці B . Декартові координати x, y |
|
виражаються через полярні координати , за формулами
x cos ,
y sin .
Тоді диференціал дуги кривої має вигляд
dl 
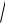 ( ( ))2 ( ( ))2d ,
( ( ))2 ( ( ))2d ,
а для обчислення криволінійного інтеграла маємо формулу
|
|
Лекція 8. Криволінійний інтеграл першого роду |
|
|
|
7 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
f(x, y)dl f ( ) cos , ( ) sin |
2 |
( |
|
2 |
|
(8.9) |
|
|
( ( )) |
( )) d . |
|||||||
|
AB |
1 |
|
|
|
|
|
|
|
Приклад 8.1.
Нехай крива
Вивести формулу dl 
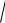 ( ( ))2 ( ( ))2d диференціала дуги кривої в полярних координатах.
( ( ))2 ( ( ))2d диференціала дуги кривої в полярних координатах.
AB задана рівнянням ( ). Якщо в рівностях
x cos ,
y sin ,
які описують зв’язок між полярними і декартовими координатами, параметром вважати кут , то криву AB можна задати параметрично
x ( ) cos ,
y ( ) sin .
Тоді
x ( ) cos ( ) sin ,
y ( ) sin ( ) cos ,
а з формули (8.6) маємо
dl 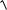
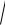 (x )2 (y )2d
(x )2 (y )2d

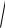 ( ) cos ( ) sin 2 ( ) sin ( ) cos 2d
( ) cos ( ) sin 2 ( ) sin ( ) cos 2d

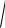 ( ) 2 ( ) 2d .
( ) 2 ( ) 2d .
8.2.2.Криволінійний інтеграл першого роду для просторових кривих
Означення і властивості криволінійного інтеграла першого роду, які сформульовані для плоских кривих, переносяться і на випадок просторової кривої AB .
Нехай кусково-гладка крива AB задана параметричними рівняннями
|
|
|
|
x x(t), |
|
|
|
|
t , |
y y(t), |
|
|
|
|
|
z z(t), |
|
|
|
функція |
f (x, y, z) |
визначена і неперервна на кривій |
AB , точці A відповідає |
||||||||||
значення |
t , |
а |
точці |
B — t . Тоді |
існує |
криволінійний інтеграл |
|||||||
f(x, y, z)dl і справджується формула |
|
|
|
|
|
|
|
||||||
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
2 |
|
|
|
|
|
f(x, y, z)dl |
f |
|
|
|
|
|
(8.10) |
||||
|
(x(t), y(t), z(t)) x (t) y (t) |
z (t) dt. |
|||||||||||
|
AB |
|
|
|
|
|
|
|
|
|
|
|
|

8 |
Лекція 8. Криволінійний інтеграл першого роду |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dl |
|
|
|
Приклад 8.2. |
|
Обчислити криволінійний інтеграл |
|
|
, де |
|||
|
|
|
|
x2 |
y2 |
||||
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x a cos t, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 t 2 . |
|
|
|
|
|
|
|
|
L : y a sin t, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z at. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для обчислення криволінійного інтеграла першого роду вздовж просторової кривої застосуємо формулу (8.10). Знайдемо похідні
xt a sin t, yt a cos t, zt a.
Тоді
dl 
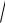 xt2 yt2 zt2dt
xt2 yt2 zt2dt 
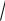 a2 sin2 t a2 cos2 t a2dt a
a2 sin2 t a2 cos2 t a2dt a 
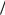 2dt.
2dt.
Отже,
|
|
dl |
2 |
a |
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
2 |
2 |
2 |
|
|||||||||||
|
|
|
|
|
|
dt |
|
|
|
dt |
|
|
|
. |
||
x2 |
y2 |
a2 |
cos2 t a2 sin2 t |
a |
|
a |
||||||||||
L |
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
||
