5. Скалярное произведение векторов

Скалярным произведением векторов иназывается число, равное произведению их модулей на косинус угла между ними. Обозначаться скалярное произведение может:,, или (,).

Пример 1.15. Вычислите скалярное произведение векторови.

Решение.Известно, что скалярное произведение векторов равно сумме произведений их соответствующих координат. Следовательно,.

Ответ: .

Пример 1.16. Найдите косинус угла между векторамии, если: а)(5, 4, –2),(–2, 1, 2); б)(3, –3, –6),(–1, 1, 2); в)(1, 2, –1),(3, 4, 11).

Решение.По определению скалярного произведения имеем равенство, значит, т. е..

а) Подставим данные: ====.

б) ====. В этом случае косинус угла равен –1, значит, угол между векторами составляет 180и они противоположно направленные. Действительно,= –3, т. е. векторы коллинеарные, а раз множитель отрицателен, то они противоположно направленные.

в) . В этом случае косинус угла равен 0, т. е. угол между векторами составляет 90, и они ортогональны.

Пример 1.17.Зная векторы, образующие треугольникABC:,,, найти углы этого треугольника.

Решение.Для того чтобы найти углы заданного треугольника надо найти косинусы углов между векторами, образующими треугольник. Это можно сделать, используя определение скалярного произведения. Но косинус угла определен для векторов, имеющих общее начало.

Угол АтреугольникаABC равен углу между векторамии. Можем найти его косинус: == =. Значит, .

Чтобы найти косинус угла ВтреугольникаABC надо искать косинус угла между векторамии(рис. 1.18). Зная что,(–2, 6), имеем =====. Значит, .

Косинус угла СтреугольникаABC есть косинус угла между векторамии(рис. 1.18), гдеи(–3, 1), а,(–1, –7). Итак, =====. Следовательно, .

Ответ: , , .

Пример 1.18. При каком значениивекторыиортогональны?

Решение. Два вектора ортогональны друг другу, если угол между ними составляет 90. Следовательно, косинус угла между ними должен быть равен нулю и, если сами векторы не нулевые, то скалярное произведение равно нулю. Запишем на математическом языке условие ортогональности (перпендикулярности) двух векторов:. Подставим данные:. Из уравнения 2+2+2=0 имеем:.

Ответ: .

Пример 1.19. В плоскостиXOZнайти вектор, перпендикулярный векторуи имеющий одинаковую с ним длину.

Решение.Пусть векторимеет координаты (x, y, z). В плоскостиXOZ лежат все такие точки и векторы, у которых вторая координата равна нулю. Т. е..

Из того, что следует. Можем теперь составить уравнение, зная, что, получим.

По условию длины векторов иравны, т. е.=.

Составим уравнение , из которого, зная что, получим.

Решим полученные уравнения вместе: или

Видим, что условию удовлетворяют два вектора, являющиеся противоположно направленными: и.

Ответ: .

6. Векторное произведение векторов

Векторным произведением векторовиназывается третий вектор(рис. 1.19), если верны следующие условия:

1. ;

2. и;

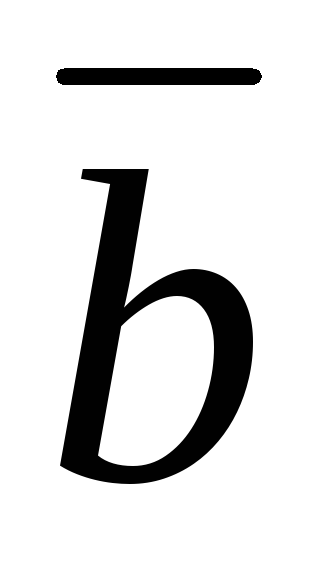3. ,,образуют правую тройку.

Обозначается векторное произведение: .

Векторное произведение векторов не коммутативно, т. е. нельзя переставлять сомножители векторного произведения.

Пример 1.20. Вычислите векторное произведение векторови.

Решение.Векторное произведение векторов вычисляется по формуле:, где,,– базисные вектора (орты),– координаты вектора,– координаты вектора.

В задаче (–1, 7, 3),(1, 8, –2), значит. Вычислим определитель:==. Таким образом,=.

Ответ: (–38, 1, –15).

Пример 1.21. Найдите площадь параллелограмма, построенного на векторахи, как на сторонах.

Решение.Модуль векторного произведения векторов численно равен площади параллелограмма, построенного на этих векторах, как на сторонах. Действительно,, а правая часть этого равенства есть формула площади параллелограмма, построенного на этих векторах, как на сторонах (рис. 1.19). Следовательно, искомая площадьS=.

В задаче (1, –1, 2),(2, –3, –1), значит. Вычислим определитель:==.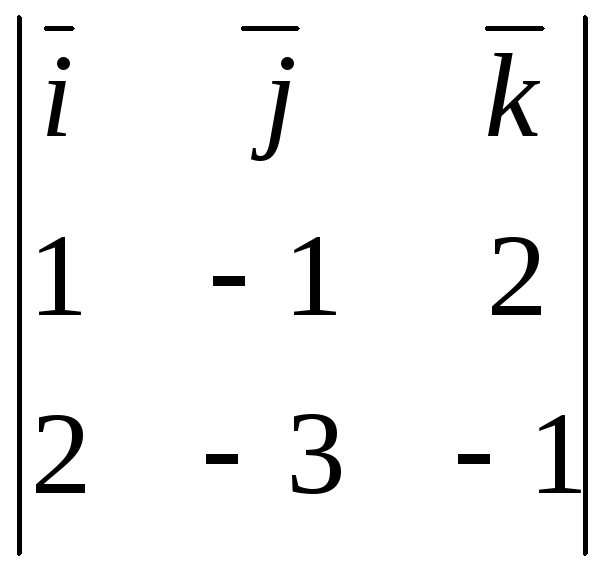

Таким образом, =. Найдем модуль полученного векторного произведения:==. Т. е. площадь параллелограмма равнамасштабных единиц в квадрате.

Ответ: S=кв. ед.

Пример 1.22. Зная векторы, образующие треугольникABC:,,, найти длину высоты этого треугольника, опущенной из точкиВ.

Решение. Для нахождения длины высоты воспользуемся формулами площади треугольника. С одной стороны площадь треугольника равна половине произведения основания на высотуS=(рис. 1.20), а с другой – половине площади параллелограмма, построенного на векторах, как на сторонах, т. е. половине модуля векторного произведенияS=.

Вычислим== =.

Найдем модуль полученного векторного произведения: = ===. Т. е. площадь треугольникаABCравнамасштабных единиц в квадрате,S=.

Найдем длину стороны АС, она равна модулю соответствующего вектора:. Тогда(ед.)

Ответ: .