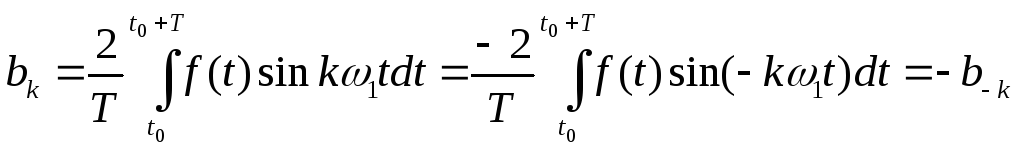pechat
.doc|
1. Понятие о токе, напряжении, мощности, энергии. Электрическим током называется упорядоченное движение частиц - носителей тока. Постоянный ток – ток неизменимый во времени. Электрический ток характеризуется силой тока.
При перемещении элементарного заряда выделяется следующая энергия:
|
2. Идеализированный резистивный элемент электрической цепи и его характеристики.
Резистивный
элемент характеризуется своим
сопротивлением.
G
– проводимость =
|
3. Идеализированный индуктивный элемент электрической цепи и его характеристики. Индуктивность
— идеализированное устройство, имеющее
два зажима, единственным ЭМ процессом
в котором является запасание и полный
возврат энергии магнитного поля.
Отсюда следует, что для описания
индуктивности используется ее
ампер-веберная характеристика
Если
речь идет о линейной индуктивности,
то
где
коэффициент L называют индуктивностью.
Размерность [L] = Гн. Можно также записать
соотношение для линейной емкости в
интегральной форме: Сделав те же подстановки, что и для емкости, получим
Положив
(что вполне естественно) I(−∞) = 0,
получим Мощность
при этом равна и может быть как положительной, так и отрицательной. Таким образом, индуктивность запасает магнитную энергию и полностью ее отдает.
Обозначение индуктивности
|
4. Идеализированный емкостной элемент электрической цепи и его характеристики. Емкость
— идеализированное устройство, имеющее
два зажима, единственным ЭМ процессом
в котором является запасание и полный
возврат электрической энергии. Отсюда
следует, что емкость описывается
вольт-кулоновой характеристикой
Если
мы рассматриваем линейную емкость ,
то
где коэффициент C называют емкостью. Размерность [C] = Ф. Можно также записать соотношение для линейной емкости в интегральной форме
Энергия
емкости Положив,
что вначале емкость не была заряжена:
и может быть как положительной, так и отрицательной. Т.е., емкость запасает электрическую энергию и полностью ее отдает.
Обозначение емкости
|
||||
|
5. Понятие об идеальном и реальном источниках напряжения.
Реальные
источники электрической энергии имеет
ЭДС
1.
2.
Пусть
|
6. Понятие об идеальном и реальном источниках тока.
Реальные
источники электрической энергии имеет
ЭДС
1.
2.
Пусть
|
7. Эквивалентные преобразования источников. Эквивалентным называется преобразование, при котором напряжения и токи в частях схемы, не подвергшихся преобразованию, не меняются.
|
8. Преобразование соединений звездой в соединение треугольником и обратное преобразование. Соединение 3-х сопротивлений, имеющие вид трелучевой звезды называется соединением ЗВЕЗДА, а соединение 3-х сопротивлений так, что они образуют собой стороны треугольника – соединением ТРЕУГОЛЬНИК. Если преобразование выполнить так, что при одинаковых значениях потенциалов одноименных точек треугольника и звезды подтекающие к этим точкам токи одинаковы, то вся внешняя схема не заметит замены. Преобразовать треугольник в звезду – значит заменить три сопротивления, соединенных в треугольник между какими-то тремя узлами, другими тремя сопротивлениями, соединенными в звезду между теми же точками. При этом на участках схемы, не затронутых этими преобразованиями, токи должны остаться неизменными.
|
||||
|
9. Теорема замещения. После вычисления тока и напряжения какой-либо ветви, для вычисления токов (напряжений) остальных ветвей полезно использовать теорему замещения. Любая ветвь цепи с током ik и напряжением uk для расчетных целей может быть заменена либо на ИТ с током ik , либо ИН с напряжением uk, при этом режим останется прежним.
|
10. Метод узловых напряжений. Особенность составления уравнений узловых напряжений при наличии ветвей с идеальными источниками напряжения. Порядок расчета: 1. Преобразовать ИН в ИТ (если возможно)
2.
Расставить узлы преобразованной цепи
(каждому узлу соответствует его
3. Составить систему независимых уравнений:
4.
Решить систему и определить напряжения
(токи) цепи.
5. Вернуться к исходной цепи. |
11. Метод контурных токов. Особенность составления уравнений контурных токов при наличии ветвей с идеальными источниками тока. Порядок расчета: 1. Выбрать направления и задать номера контурных токов. Если есть ИТ, то номер контурного тока, проходящего через ИТ, рекомендуется задавать последним. Через ИТ должен проходить только один контурный ток! 2. Составить систему независимых уравнений:
3.
Решить систему и определить напряжения
(токи) цепи.
|
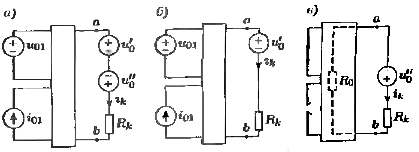
12. Теоремы об эквивалентных источниках; теоремы Тевенена и Нортона. Теорема Тевенена (об эквивалентном источнике): Любую активную цепь с двумя полюсами (зажимами) в установившемся режиме можно заменить источником напряжения и последовательно включенным сопротивлением.
В
цепи (рис б) требуется найти ток ik
в одной из ветвей с сопротивлением
Rk,
причём источники вынесены наружу.
Заменим всю цепь, по отношению к
двухполюснику Rk,
одним источником напряжения u0
и последовательно включенным
сопротивлением R0
так, чтобы режим работы Rk
не изменился (рис в). Если замена
возможна, то
Док-во:
(рис а)
Теорема Нортона. Любой активный двухполюсник можно заменить эквивалентным источником тока с некоторой внутренней проводимостью. (эта теорема дуальна к прошлой, доказывается аналогично) |
||||
|
13. Теорема взаимности. Пользуясь метолом контурных токов, установим еще одно важное свойство линейных электрических цепей — свойство взаимности, или, как его еще называют, принцип взаимности.
В схеме произвольной конфигурации единственный источник ЭДС Еq действует в ветви с сопротивлением rq в направлении от точки b к точке a (рис. а) и создает в ветви с сопротивлением rl ток Il направленный от точки d к точке с. Т Здесь ветвь cd является частью контура l, а ветвь ab входит в состав другого контура q (рис. а), и, как указано, других источников, кроме источника ЭДС Еq, эта цепь не содержит. Контуры выбраны так, чтобы ab и cd вошли каждая в один контур, соответственно q и l. Ток в контуре l, равный току ветви dc,
D(K) - определитель системы уравнений, Dlq - его алгебраическое дополнение, которое получается вычеркиванием из D(K) 1-го столбца и q-й строки и умножением полученного определителя на (-1)l+q. Если источник ЭДС Еq переставить в ветвь cd контура l (рис. 5.3, б) то в правой части системы (5.4) в q-й строке будет 0, а в l-й строке будет Еq. Тогда ток Iq в контуре q, т. е. ток в ветви ab, В отличии от Dlq, алгебраическое дополнение вида Dql получается из определителя D(K) вычеркиванием столбца q и строки l и умножением получаемого определителя на (-1)l+q. Так как в контурных уравнениях общие сопротивления rlq, и rql равны друг другу, то и Dlq=Dql. Следовательно, при равенстве ЭДС Еl=Еq токи в ветвях cd (рис. а) и ab (рис. б) равны друг другу. Свойство взаимности справедливо не только для токов, но и для напряжений. |
13. Первый и второй законы коммутации в электрических цепях.
Закон
коммутации для индуктивного элемента:
Закон
коммутации для емкостного элемента:
При
|
14. Свободный процесс в RL-контуре. Метод подкасательной для определения постоянной времени переходного процесса в электрической RC- и RL-цепи.
ХП
(характ. полином):
|
15. Включение последовательного RL-контура к источнику постоянного напряжения. Вычисление энергии, выделяемой в R-элементе при переходном процессе.
|
||||
|
16. Включение параллельного RC-контура к источнику постоянного тока (по принципу дуальности).
|
17. Определение порядка электрической RLC-цепи. Особый случай коммутации RC-цепи (пример анализа переходного процесса при подключении незаряженной емкости к зараженной емкости).
Порядок
цепи
– это максимальная степень
дифференциального уравнения. Во многих
случаях порядок равен сумме накопительных
элементов ( |
18. Анализ апериодического переходного процесса в последовательном колебательном RLC-контуре при воздействии постоянного источника напряжения.
|
19. Анализ колебательного переходного процесса в последовательном колебательном RLC-контуре при воздействии постоянного источника напряжения.
Колебательный
режим
|
||||
|
20. Анализ критического переходного процесса в последовательном колебательном RLC-контуре при воздействии постоянного источника напряжения.
Критический
режим
|
21. Составление системы дифференциальных уравнений с использованием переменных состояния.
ДУ
Общий
вид:
Вспомогательная система:
|
22. Аналитическое решение системы дифференциальных уравнений в форме переменных состояния.
1.
2.
3.
4.
5.
Ак:
ПС - перем. состояние, СВ - своб., ВЫН – вынужд., ХП – характеристич. полином
|
23. Определение единичных ступенчатой и импульсной функций. Некоторые стандартные сигналы, на которые необходимо находить отклики (из них можно выразить все остальные).
Используется для выделения функции в некотором времени.
|
||||
|
24. Связь между единичными импульсной и ступенчатой функциями.
|
25. Переходная и импульсная характеристики электрической цепи. Связь между импульсной и переходной характеристиками электрической цепи. Переходная
характеристика
Импульсная
характеристика:
Характеристика
|
26. Интеграл свертки (интеграл наложения, выраженный через импульсную характеристику электрической цепи).
Пусть
реакции,
получим
Интеграл
свертки:
|
27. Интеграл Дюамеля (интеграл наложения, выраженный через переходную характеристику электрической цепи).
Пусть
реакции,
получим
Интеграл
свертки:
Интеграл
Дюамеля:
|
||||
|
28. Нормирование параметров элементов электрической цепи. |
29. Синусоидальные сигналы и их основные параметры. Синусоидальными сигналами или воздействиями называются переменные напряжения и токи источников, которые аналитически можно записать с помощью синусоидальной функции в синусной или косинусной форме:
Как
правило, в теории электрических цепей
синусоидальные функции напряжений и
токов записывают в косинусной форме,
поскольку косинус функция четная и с
ней проще оперировать. В записанных
выражениях Um
и Im
амплитудные
значения напряжения и тока,
|
30. Среднее и действующее значения синусоидальных токов и напряжений.
Среднее
за период T
значение
определяется как
|
31. Метод комплексных амплитуд. Законы Кирхгофа в комплексной форме. Формы записи комплексного числа:
Закон токов Кирхгофа:
Закон напряжения Кирхгофа:
Проводя
аналогичные рассуждения
|
||||
|
32. Характеристики резистивного элемента при установившемся синусоидальном режиме. R-элемент и его схема замещения в комплексной форме.
Для определения комплексного сопротивления и комплексной проводимости R-элемента выразим синусоидальный ток, условно протекающий в нем через напряжение и сопротивление, руководствуясь при этом вольт-амперной характеристикой R-элемента:
из полученного равенства можно получить выражение для комплексного сопротивления резистора:
Из записанных выражений можно сделать вывод: в R-элементе ток и напряжения совпадают по фазе. Аналогично можно получить выражение для комплексной проводимости:
Мгновенная мощность R-элемента определяется произведением тока на напряжения, или:
|
33. Характеристики индуктивного элемента при установившемся синусоидальном режиме. L-элемент и его схема замещения в частотной (комплексной) области
Для определения комплексного сопротивления и комплексной проводимости L-элемента выразим синусоидальное напряжение на нем через ток, руководствуясь при этом вольт-амперной зависимостью L-элемента:
Разделив комплексную амплитуду напряжения на комплексную амплитуду тока можно получить выражение для комплексного сопротивления L-элемента:
Из записанных выражений можно сделать вывод: в L-элементе ток отстает от напряжения на угол 900. Аналогично можно получить выражение для комплексной проводимости:
Мгновенная мощность L-элемента определяется произведением тока на напряжения, или:
Временные диаграммы напряжения, тока, мощности и энергии L-элемента
Мгновенная энергия определяется из выражения:
|
34. Характеристики емкостного элемента при установившемся синусоидальном режиме. C-элемент и его схема замещения в частотной (комплексной) области.
Для определения комплексного сопротивления и комплексной проводимости C-элемента выразим синусоидальное напряжение на нем через ток исходя из его вольт-амперной характеристики:
Из записанных равенств можно получить выражение для комплексного сопротивления C-элемента:
Из записанных выражений можно сделать вывод: в C-элементе ток опережает напряжение на угол 900. Аналогично можно получить выражение для комплексной проводимости:
Мгновенная мощность С-элемента определяется произведением тока на напряжения, или:
Мгновенная энергия определяется из выражения:
|
35. Расчет индуктивного, емкостного, резонансного режимов работы в последовательном RLC-контуре. Построение потенциальной векторной диаграммы напряжений ветвей контура.
1.
2.
3.
|
||||
|
36. Расчет мгновенной мощности в двухполюснике при установившемся синусоидальном режиме. Пусть
через элемент течет ток
Активная
мощность:
Реактивная
мощность:
Активная
мощность зависит от
|
37. Вычисление мощности двухполюсника в комплексной форме. Мгновенную мощность двухполюсника можно определить, как произведение напряжения на ток:
Это означает, что мгновенная мощность пассивного двухполюсника будет являться синусоидальной функцией с удвоенной частотой. Временные диаграммы тока, напряжения и мощности:
Преобразуем полученное выражение для мгновенной мощности по формулам приведения:
В результате проделанных преобразований мгновенную мощность удалось представить в виде суммы двух составляющих:
Мощности пассивного двухполюсника можно выразить через параметры комплексного сопротивления:
В комплексной форме полная мощность представляется как комплексное выражение, у которого вещественная часть представляет собой активную мощность, а мнимая часть – реактивную мощность:
|
38. Улучшение коэффициента мощности двухполюсника с помощью конденсатора.
При
возрастании
|
39. Условие согласования генератора с нагрузкой. Условие передачи максимальной мощности от источника к нагрузке.
Кпд
|
||||
|
4 Электрическим резонансом в электрических цепях называется такое явление, при котором ток и напряжение на входе цепи в синусоидальном установившемся режиме совпадают по фазе. Такое явление можно наблюдать в том случае, если Im[ZВХ]=0 или Im[YВХ]=0. Поэтому в цепях различают резонанс в последовательном контуре (резонанс напряжений) или в параллельном контуре (резонанс токов).
Резонанс
в последовательном колебательном
контуре.
В момент резонанса мнимая часть
комплексного сопротивления в таком
контуре равна нулю Im[Z]=0.
Сопротивления реактивных элементов колебательного контура зависят от частоты, следовательно, эти зависимости можно построить в функции частоты. Вертикальная линия на рисунке отмечает равенство модулей сопротивлений индуктивного и емкостного элементов, что соответствует частоте резонанса в контуре. Резонанс в параллельном колебательном контуре. Параллельный колебательный контур дуален последовательному, и все процессы в нем схожи с процессами в последовательном контуре. В
П |
41. Частотные характеристики последовательного RLC-контура и нормирование его характеристик.
|
42. Определение полосы пропускания последовательного RLC-контура по его амплитудно-частотной характеристике.
|
43. Включение RL-контура к источнику синусоидального напряжения.
|
||||
|
44. Прямое преобразование Лапласа. Основные его свойства. Изображения функций: единично- ступенчатой, импульсной, синусоидальной, косинусоидальной, экспоненциальной, линейно-нарастающей. Изображение периодических сигналов.
Алгебраическую сумму трактуем как последовательное соединение элементов
Уравнение параллельного соединения
Вывод: операторные схемы эквивалентны, они соответствуют правилам эквивалентных преобразований ИТ или ИН и удовлетворяет законам Кирхгофа.
|
45. Операторные схемы замещения индуктивного элемента электрической цепи.
|
46. Операторные схемы замещения емкостного элемента электрической цепи.
|
47. Обратное преобразование Лапласа. Теорема разложения для случаев простых вещественных полюсов изображения.
Так
как
Теорема разложения для Простых вещественных полюсов.
Коэфиценты А1, А2,…,Аn – вычеты
Положим S=Sk, то есть:
|
||||
|
48. Обратное преобразование Лапласа. Теорема разложения для случаев комплексных полюсов изображения.
Так
как
Теорема разложения для Комплексной Байдыыыыыы:
Формула справедлива и для комплексных чисел.
А2=А1 Воспользуемся формулой (3)
В случае наличия двух комплексных сопряж. полюсов в реакции имеется гарм. Функция, затухающая по е.
|
49. Обратное преобразование Лапласа. Теорема разложения для случаев простых кратных полюсов изображения.
Так
как
Простая кратная прохерь:
Для
нахождения А1 обе части домножим на
После
подстановки
Продифференцируем обе части выражения (4) по S:
Выполним
подстановку
|
50. Операторная передаточная функция цепи и связь ее с изображениями переходной и импульсной характеристик.
|
51. Точный расчет реакции электрической цепи при установившемся периодическом воздействии.
|
||||
|
52. Тригонометрическая и косинусная формы записи разложения периоди- ческих сигналов в ряд Фурье. Связь между коэффициентами этих рядов.
Тригонометрическая
форма:
Косинусная форма:
|
53. Расчет активной мощности электрической цепи в установившемся несинусоидальном режиме.
где
|
54. Действующее значение периодических несинусоидальных токов и напряжений.
где
|
55. Общая методика расчета установившегося несинусоидального режима электрической цепи.
|
||||
|
56. Комплексная форма ряда Фурье.
|
57. Понятие о комплексной спектральной характеристике и комплексной амплитуде периодического несинусоидального сигнала. Спектр сигнала - совокупность синусоидальных составляющих с различными частотами Математической базой для спектрального представления сигналов являются аппарат рядов Фурье для периодических функций и интегралов Фурье — для непериодических. Анализ цепи под действием каждой отдельной синусоидальной составляющей производится с помощью уже изученных методов (например, комплексного метода). Для нахождения временной зависимости искомой величины используют принцип наложения. Описанный подход и составляет частотный (спектральный) метод расчета цепи. Сигнал, обладающий свойством периодичности f(t)=f(t + T ) , удовлетворяющий условиям Дирихле, может быть представлен в виде ряда Фурье:
Записанное f(t) определяет тригонометрическую форму ряда Фурье. Наиболее компактной и удобной для расчетов формой записи является экспоненциальная (комплексная) форма ряда Фурье.
Комплексные
коэффициенты позволяют непосредственно
выразить амплитуды гармоник и их
начальные фазы
|
58. Спектры непериодических сигналов и их преобразование по Фурье. Интеграл Фурье. Переход
от спектрального представления
периодического сигнала к непериодическому
можно осуществить, выполняя в полученных
соотношениях комплексной формы
ряда Фурье для сигналов с периодом T
предельный переход к
Переходя
к пределу при
|
59. Связь преобразований непериодических сигналов по Фурье и Лапласу.
|
||||
|
60. Связь спектральных характеристик одиночного импульса и периодической после-довательности импульсов.
|
61. Спектральная характеристика одиночного прямоугольного импульса. Ширина спектра этого сигнала.
|
62. Амплитудный и фазовый спектры периодической последовательности прямоугольных импульсов. Представление рядом Фурье периодической последовательности прямоугольных импульсов.
|
63. Вычисление частотных характеристик электрических цепей. Экспериментальное определение этих характеристик.
|
||||
|
64. Частотные характеристики электрической цепи, передающей электрический сигнал без искажения. Понятие о полосе пропускания электрической цепи.
|
65. Частотные характеристики идеальной дифференцирующей цепи.
|
66. Частотные характеристики реальной дифференцирующей RC-цепи.
|
67. Реакция реальной дифференцирующей RC-цепи на линейно-возрастающее воздействие.
|
||||
|
68. Частотные характеристики идеальной интегрирующей цепи.
|
69. Частотные характеристики реальной интегрирующей RC-цепи.
|
70. Переходная характеристика реальной интегрирующей RC-цепи.
|
© Жуковский Артём, Астахов Антон, Мездрогин Дима Новик Саша Сорокин Андрей Сделано для группы 6151 (http://6151.spb.ru) |



 (по
закону Кирхгофа)
(по
закону Кирхгофа)

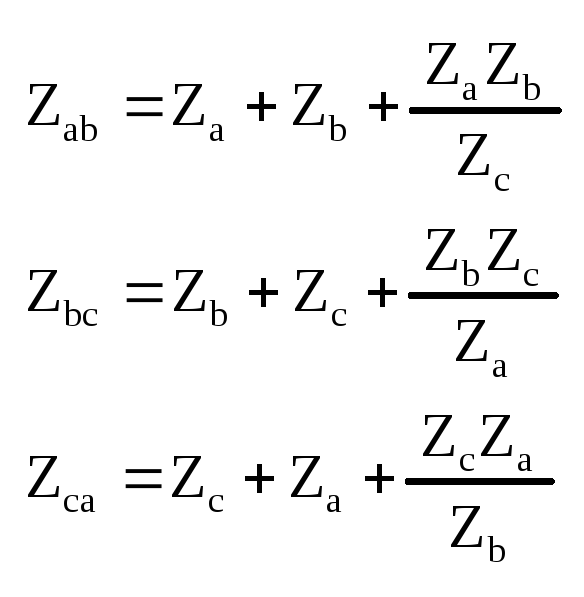

 ,
где
,
где
 ,
где
,
где

 акой
же единственный источник ЭДС Еl=Еq,
включенный в ветвь с сопротивлением
rl и действующий в направлении от d к с
(рис. б), создаст в ветви с сопротивлением
rq ток Iq, направленный от b к a и равный
току Il.
акой
же единственный источник ЭДС Еl=Еq,
включенный в ветвь с сопротивлением
rl и действующий в направлении от d к с
(рис. б), создаст в ветви с сопротивлением
rq ток Iq, направленный от b к a и равный
току Il.




 ,
,




 .
Свойство:
.
Свойство:
 .
Свойства:
.
Свойства:




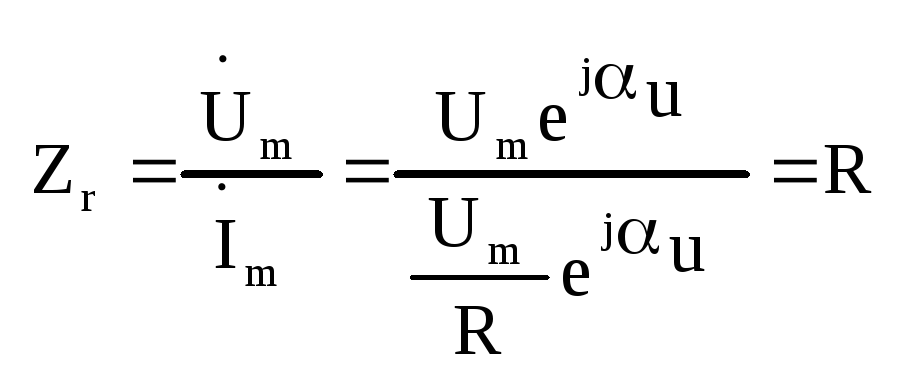 ,
,




 ,
,





 ,
для
мах
,
для
мах