4. Правило Лопиталя – Бернулли.

При исследовании функций может появиться необходимость нахождения предела дроби , числитель и знаменатель которой пристремятся к нулю или бесконечности. Для нахождения таких пределов бывает удобно воспользоваться следующим правилом:

Теорема. Если функции идифференцируемы в окрестности точки, обе или обращаются в нуль в этой точке, или стремятся к бесконечности и существует предел отношенияпри, тогда существует предел отношения самих функций, равный предел отношения производных.

.

Замечание 1. Теорема верна и в том случае, когда функции ине определены в точке, ноили.

Замечание 2. Теорема верна и в случае , т.е. когдаили

Другими словами правило Лопиталя – Бернулли применяется для раскрытия неопределенностей типа и.

С помощью тождественных преобразований к основному виду иможно свести неопределенности других видов, таких как.

При выполнении соответствующих условий правило Лопиталя – Бернулли можно применять несколько раз.

Пример 2.24. Найти.

Решение. Найдем значения функций, стоящих в числителе и знаменателе при:

.

.

Так как обе функции дифференцируемы в окрестности точки , то применим правило Лопиталя – Бернулли.

[Подставимв получившиеся в числителе и знаменателе функции,] = –1.

Ответ: {–1}.

Пример 2.25. Найти.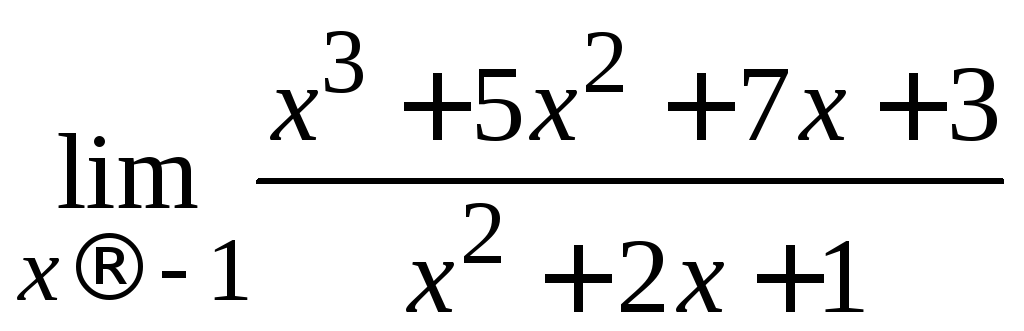

Решение. Найдем значения функций, стоящих в числителе и знаменателе при:

.

.

Так как обе функции дифференцируемы в окрестности точки , то применим правило Лопиталя – Бернулли.

; [ Подставимв получившиеся в числителе и знаменателе функции,]. Так как неопределенностьсохранилась, и функции получившиеся в числителе и знаменателе опять удовлетворяют условиям теоремы (2.1), то можно применить правило Лопиталя – Бернулли еще раз.

.

Ответ: {2}.

Пример 2.26. Вычислить.

Решение. Проверкой убеждаемся, что функции, стоящие в числителе и в знаменателе обращаются в нуль при. Так ак они обе непрерывно дифференцируемы, то применяем правило Лопиталя – Бернулли:

.

Ответ: .

5. Формула Тейлора.

Одной из важнейших формул математического анализа несомненно является формула Тейлора, которая широко применяется и как инструмент теоретического исследования и как средство решения многих практических задач.

Формула Тейлора позволяет приближенно представить произвольную функцию в виде многочлена и вместе с тем позволяет оценить возникающую при этом погрешность , которая может быть сделана сколь угодно малой.

Вычисление значений функции при этом сводится к вычислению значений многочлена, что можно сделать, производя только простейшие арифметические действия.

Теорема Тейлора. Функция , дифференцируемаяраз в некотором интервале, содержащем точку, может быть представлена в виде суммы многочленаn-ой степени и остаточного члена, а именно:

, где– остаточный член в форме Пеано, бесконечно малая величина по сравнению с.

Напомним, что операция факториал определяется следующим образом:

;

;

;

0!=1

Если , то формула принимает вид:

и называется формулой Маклорена, однако для многих функций она неприменима, так как сами функции или их производные не существуют при(например:Ф).

Напомним, что частный случай замены функции многочленом был уже рассмотрен в п (1.5), где рассматривалось применение дифференциала к приближенным вычислениям. Именно там функция заменялась многочленом первой степени, т.е линейной функцией. Однако эти результаты носят очень ограниченный характер, так как не дают возможность оценивать точность такой замены.

Остаточный член в формуле Тейлора можно записывать и в других формах, например Коши или Лагранжа. И выбор формы его записи обычно диктуется условиями конкретной задачи.

Пример 2.27. Разложить в ряд Маклорена функцию.

Решение.Вычислим значение данной функции и ее производных при:

Формула Тейлора для некоторых элементарных функций.

Список литературы

1. Письменный Д. Т. Конспект лекций по высшей математике: В 2 ч. М.: Айрис Пресс, 2006. Ч. 1.

2. Методы вычисления пределов: Методические указания к решению задач / Сост.: Ю. В. Крашенинникова, М. Н. Абрамова. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2008.

Содержание

1. ПРОИЗВОДНАЯ ФУНКЦИИ 4

1.1. Понятие производной, ее геометрический и физический смысл. 4

1.2. Техника дифференцирования основных элементарных функций. 6

1.3. Основные правила дифференцирования. 7

1.4. Дифференцирование показательно – степенной функции. 12

1.5. Дифференцирование неявно заданных функций и функций, заданных параметрически. 13

1.6. Производные высших порядков. 14

2. ПРИЛОЖЕНИЯ ПРОИЗВОДНЫХ 16

2.1. Дифференциал функции. 16

2.2. Применение дифференциала в приближенных вычислениях. 17

2.3. Уравнения касательной и нормали к графику функции. 18

2.4. Правило Лопиталя – Бернулли. 21

2.5. Формула Тейлора. 23

Редактор И. Г. Скачек

__________________________________________________________________

Подписано в печать Формат 6084 1/16. Бумага офсетная.

Печать офсетная. Печ. л. 2.0.

Гарнитура «Times». Тираж 250 экз. Заказ

__________________________________________________________________

Издательство СПбГЭТУ «ЛЭТИ»