4. Дифференцирование показательно – степенной функции.

Для того, чтобы найти производную показательно – степенной функции , гдеf(x) иg(x) – дифференцируемые функции отх, ее удобно предварительно прологарифмировать.

, тогда. [воспользуемся свойствами логарифма и запишем]. [теперь найдем производные от обеих частей равенства.]

.[для нахождения производной правой части воспользуемся правилом (1.3), а для левой части – правилом дифференцирования сложной функции (1.5)].

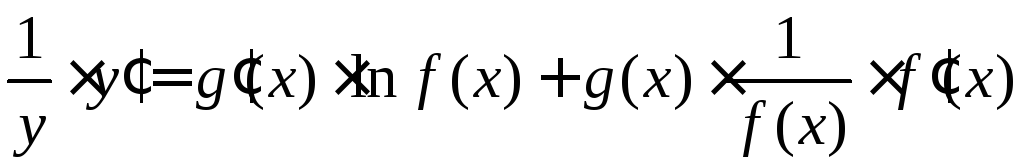. [выразим из данного равенства]

.

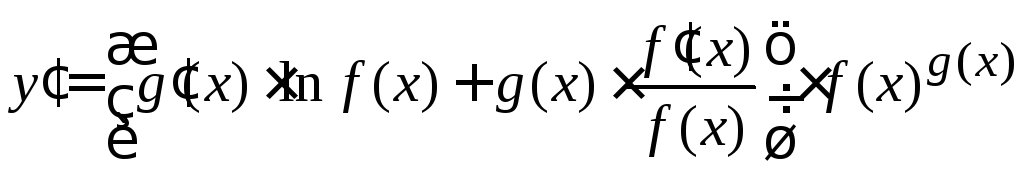Запоминать такую громоздкую формулу нет необходимости, так как правильнее, при необходимости найти производную показательно – степенной функции, каждый раз применять данный прием.

Пример 1.12. Найти производную функции.

Решение.Прологарифмируем обе части равенства:

. [воспользуемся свойствами логарифма]

. [найдем производные от обеих частей равенства]

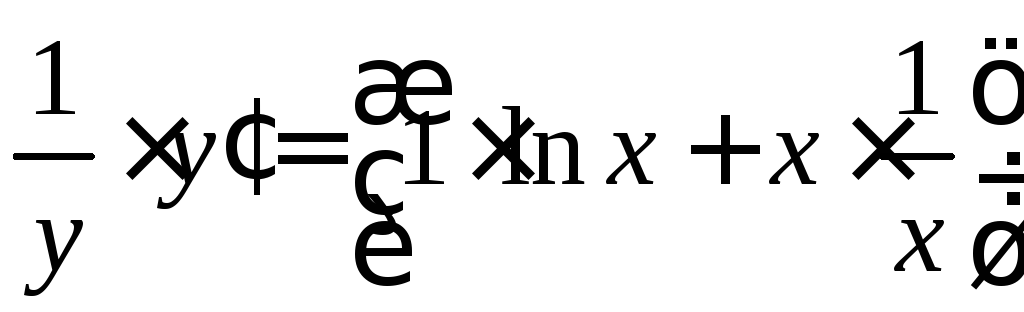. [выразим из данного равенства]

Пример 1.13. Найти производную функции.

Решение. Прологарифмируем обе части равенства:

.

. [найдем производные от обеих частей равенства]

.

.

.

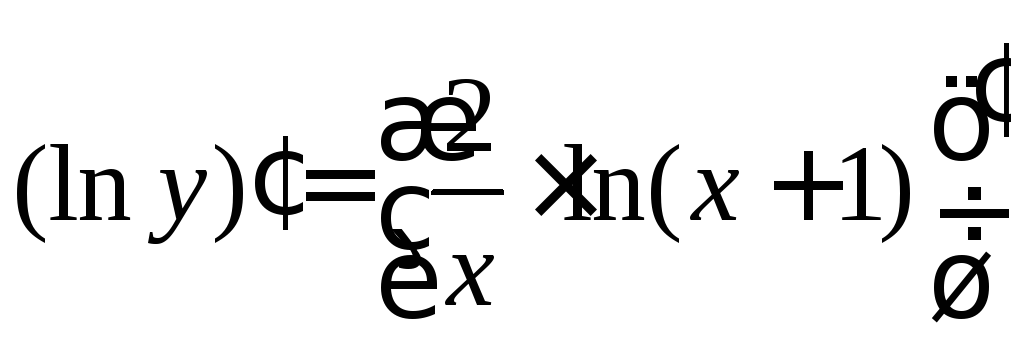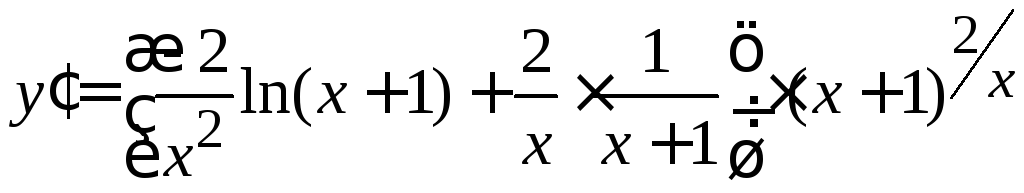4. Дифференцирование неявно заданных функций и функций, заданных параметрически.

Если зависимость между xиy задана в форме уравненияF(x,y)=0, то говорят, что функция задана неявно. В этом случае для нахождения производныхиследует продифференцировать уравнениеF(x,y)=0 поx, считаяy функцией отx , или поy, считаяxфункцией отyи выразить из полученного уравнения производнуюили.

Пример 1.3. Найдите производнуюфункции, заданной неявно.

Решение.Продифференцируем исходное уравнение, считаяy функцией отx . Дифференцируя левую часть уравнения, необходимо воспользоваться правилом (1.5), а правую – правилом (1.3).

. [выразим из данного равенства]

.

.

.

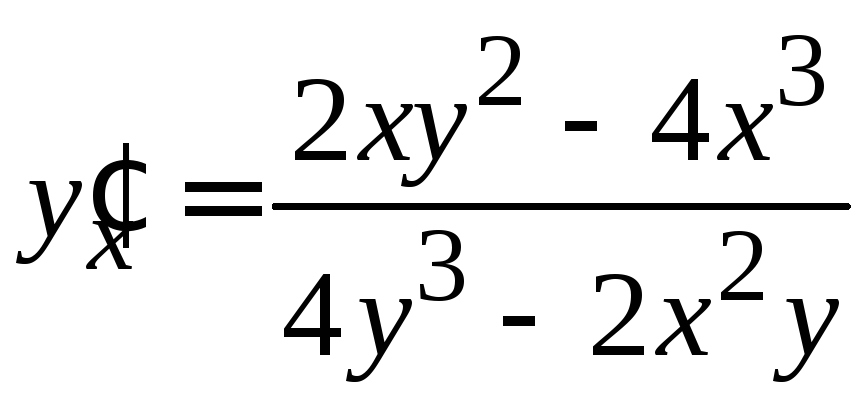Пример 1.14. Найдите производнуюзаданной неявно функции.

Решение.Продифференцируем исходное уравнение, считаяy функцией отx. Второе слагаемое в уравнения является сложной функцией, первое - произведением двух функций, одна из которых – экспонента сама является сложной. Поэтому продифференцируем каждое слагаемое отдельно, а потом запишем производную всей функции целиком.

.

В итоге получаем:

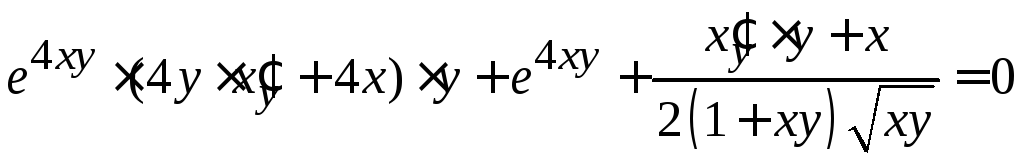. [раскрываем скобки и группируем слагаемые, содержащие производную]

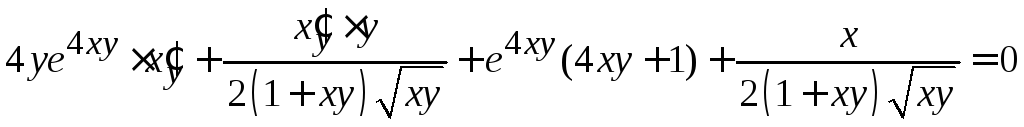. [выражаем из получившегося уравнения]

.

.

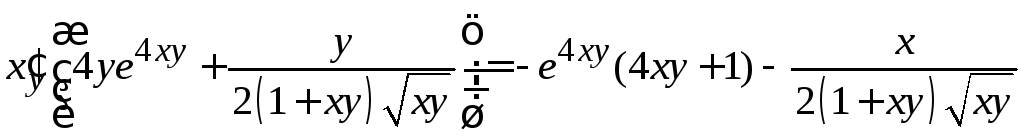6. Производные высших порядков.

Производной второго порядка, или второй производной, функции называется производная от ее производной(которую называют первой производной).

Обозначения второй производной:

.

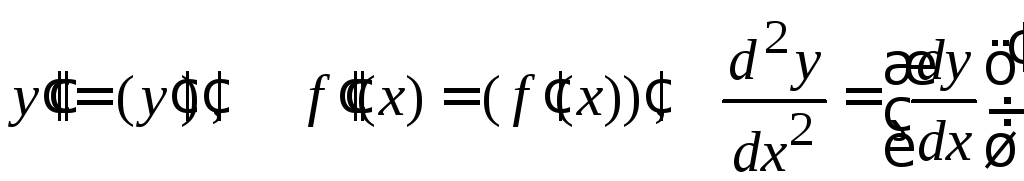Механический смысл второй производной.

Если – закон прямолинейного движения точки, то– ускорение этого движения в момент времениx.

Аналогично определяются производные третьего, четвертого и более высоких порядков:

.

Производная n–ого порядка обозначается и так:.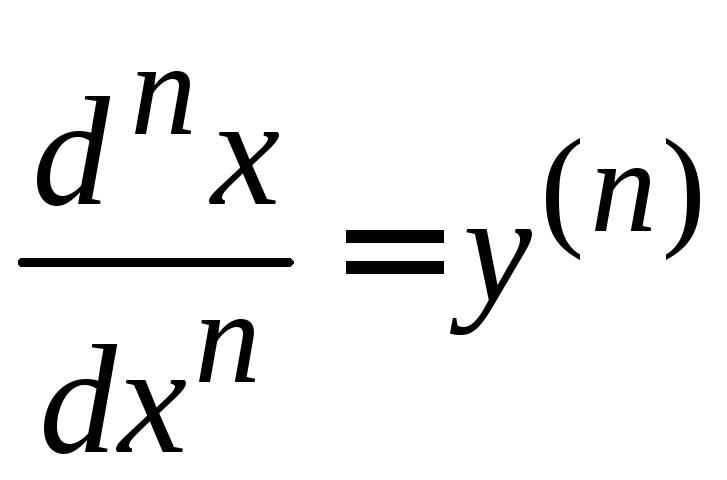

Если функция задана параметрически: , то ее вторая производная определяется формулой:

.

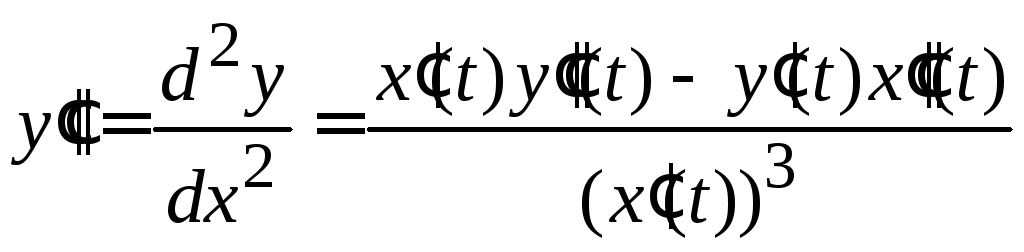Пример 1.15. Найтидля функции.

Решение. Для того, чтобы вычислить значение третьей производной функциив точке, необходимо найти первую и вторую производные этой функции.

.

.

. [Подставляем в найденное выражение третьей производной значение]

.

Ответ: {-6}.

Пример 1.16. Найти вторую производную функции, заданной параметрически:.

Решение. Найдем первую и вторую производные для функций.

.

.

Воспользуемся формулой, приведенной выше:

[воспользуемся тождеством, ].

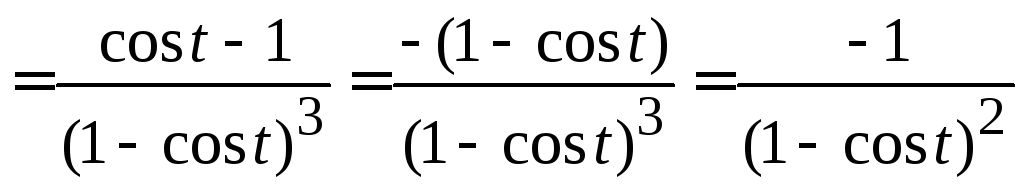Ответ: 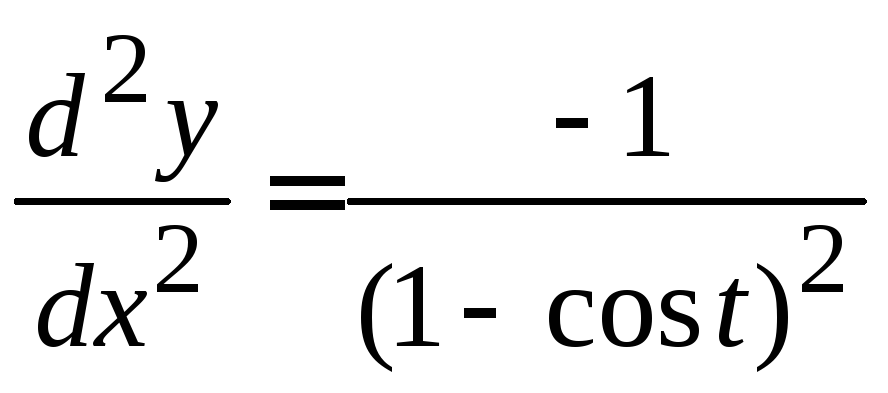.