Федеральное агентство по образованию

___________________________________

Санкт-Петербургский государственный

электротехнический университет «ЛЭТИ»

_______________________________________

Методы решения задач: техника вычисления производных.

Методические указания

к решению задач

Санкт-Петербург

Издательство СПбГЭТУ «ЛЭТИ»

2009

УДК 517.22 (077)

Методы решения задач: техника вычисления производных: Методические указания к решению задач / Сост.: М. Н. Абрамова, К. Г. Межевич, Е. А. Толкачева. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2008. 32 с.

Содержат определения, формулировки основных теорем и примеры решения задач различными методами по теме «Производная функции».

Предназначены для студентов-заочников всех специальностей.

Утверждено

редакционно-издательским советом университета

в качестве методических указаний

© СПбГЭТУ «ЛЭТИ», 2009

Настоящее издание призвано помочь студентам-заочникам младших курсов самостоятельно научиться решать задачи по теме «Производная функции». Освоение этого раздела математического анализа на первый взгляд не вызывает затруднения у студентов. Но без четкого овладения именно техникой дифференцирования и понятием производной практически невозможно дальнейшее продвижение в освоении курса математического анализа. Поэтому первая часть методических указаний посвящена подробному обсуждению понятия «производная функции» и основных правил дифференцирования. Во второй части указаний рассматривается применения производной к решению ряда наиболее часто встречающихся задач.

Данные методические указания, хоть и содержат теоретический материал, не призваны служить полной заменой учебника по теме «Производная функции», поэтому составители рекомендуют параллельно работать с учебным пособием «Конспект лекций по высшей математике» Д. Т. Письменного [1].

1.Производная функции

1.4.Понятие производной, ее геометрический и физический смысл.

П усть функция определена в интервале (a;b) и непрерывна в точке , и пусть . В окрестности точки выбирается произвольная точка x. Тогда разность называется приращением аргумента в точке . А разность – приращением функции. На рисунке рассмотрим секущую, проведенную через точки M и N. Угол называется углом наклона секущей, а ее угловым коэффициентом.

Из прямоугольного треугольника MPN . Если точка N будет стремиться к M вдоль данной линии, то есть , то секущая MN в пределе перейдет в касательную l , а угол наклона секущей – , в угол наклона касательной – .

Определение:

Производной функции в точке называется предел отношения приращения этой функции к приращению аргумента, когда последний стремится к нулю, т.е .

Геометрический смысл производной.

Из рассуждений, приведенных выше видно, что производная функции при равна угловому коэффициенту касательной к графику данной функции в точке , т.е .

Физический смысл производной.

Если – закон прямолинейного движения точки, то – скорость этого движения в момент времени t.

Быстрота протекания физических, химических и других процессов выражается с помощью производной.

Сила и импульс по второму закону Ньютона связаны соотношением:

Количество заряда, прошедшего через поперечное сечение проводника, определяет силу тока:

В электростатическом поле, изменяющемся только по оси OX, напряженность и потенциал связаны соотношением:

Если отношение при имеет предел справа (или слева), то он называется производной справа (соответственно производной слева). Такие пределы называются односторонними производными. Односторонние производные в точке обозначаются соответственно :

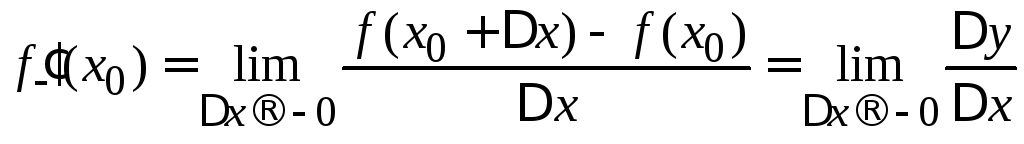– производная слева;

– производная справа.

Очевидно функция, определенная в некоторой окрестности точки , имеет производную тогда и только тогда, когда односторонние производные существуют и равны между собой, причем .

Если для некоторого значения x выполняется одно из условий

, то говорят, что в точке x существует бесконечная производная, равная соответственно .

Функция, имеющая производную в данной точке, называется дифференцируемой в этой точке. Функция, имеющая производную в каждой точке данного промежутка, называется дифференцируемой в этом промежутке.

Операция нахождения производной называется дифференцированием.

Пример 1.1. Пользуясь определением производной найти производную функции .

Решение: Зададим аргументу данной функции приращение . Тогда приращение функции . Воспользуемся определением производной:

.

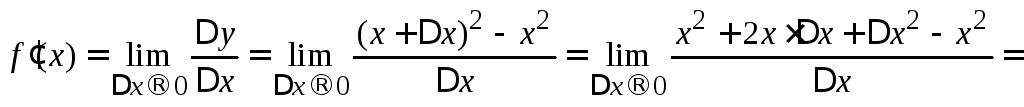
Ответ: .