7. Фазовый синтез

7.1. Актуальность для фар, постановка задачи.

Для фазированных антенных решеток задача синтеза приобретает своеобразный характер ввиду того , что сама структура и принцип действия ФАР допускают прежде всего возможность варьирования фазами излучателей и реже (например в случае АФАР) еще и

Рис. 1. Блок схема итерационного процесса

амплитудами. Поэтому задача синтеза ДН специальной формы применительно к ФАР ставится таким образом: найти такие фазы на излучателях ФАР, которые при фиксированном амплитудном распределении приводят к реализации амплитудной диаграммы направленности заданного вида. Такая постановка носит название задачи фазового синтеза.

7.2. Итерационный метод фазового синтеза. Примеры.

Для решения задач синтеза антенн с большими электрическими размерами раскрыва необходимы быстродействующие методы, одним из таких является итерационный. Принцип итерационного метода синтеза можно пояснить с помощью блок-схемы, изображенной на рис. 1. Здесь - обобщенная угловая координата (изменяется в пределах [-1,1]),- эталонная амплитудная ДН.

Сначала определяются исходные данные для синтеза ДН: электрические размеры, частота, требуемая ДН. Затем выбирается начальное АФР. Далее начинается итерационный процесс. По АФР рассчитывается комплексная ДН , если амплитудная ДН (||) удовлетворяет критерию качества (например, заданной среднеквадратической ошибке), то расчет прекращается, а искомым АФР считается используемое в последней итерации. В противном случае амплитудная ДН заменятся на эталонную(фазовая ДН не меняется), и, с помощью обратного преобразования Фурье, рассчитывается новое АФР. Далее начинается новая итерация (по полученному АФР рассчитывается, … ). В случае фазового синтеза, амплитудное распределение задано изначально и не меняется от итерации к итерации, рассчитывается только. В случае амплитудного синтеза фиксируется начальное фазовое распределение и рассчитывается только амплитудное.

С помощью указанной блок-схемы проиллюстрирована простейшая реализация итерационного метода синтеза, однако она не является оптимальной с точки зрения результата и не позволяет учитывать ограничения на АФР. Для устранения этих недостатков итерационный метод был модифицирован [4]. Для отсчетов амплитудной ДН вводятся границы допустимых значений, отсчеты не попадающие в них заменяются на, остальные остаются без изменений. То есть теперь

, (1)

где - граница дляm-го отсчета амплитудной ДН. Границей может служить, например, уровень боковых лепестков, или допустимое значение неравномерности в пределах главного лепестка. Аналогичные способом можно учесть ограничения на АФР, только теперьидолжны попадать в заданные границы.

Рассмотрим пример: необходимо синтезировать секторную ДН с шириной главного лепестка 40° на ФАР, состоящей из 23 элемента, расстояние между которыми 0.53λ. На рис. 2 показан один из вариантов задания и ограничений на значения. Еслиилито отсчетыдолжны удовлетворять условию; еслиили, то; если, то. Если отсчетыне удовлетворяют указанным условиям, то им присваиваются значения(LEV2 если). КонстантаLEV1 определят ограничения на допустимый УБЛ,LEV2 определяет нижнюю границу неравномерности в пределах главного лепестка ДН. Также существует возможность менять крутизну склонов сектора. На рис. 3 показана синтезированная ДН (системный множитель), а на рис. 4 найденное фазовое распределение. При решении,,, крутизна склонов сектора.

Рис. 2. Эталонная ДН

Рис. 3. Синтезированная ДН Рис. 4. Амплитудное и найденное

фазовое распределения

С помощью итерационного метода можно получать и другие формы ДН, например, на рис. 5 и рис. 6 показаны косекансная ДН и соответствующее АФР для антенной решетки, состоящей из 21 излучателя с межэлементным расстоянием 0.58λ.

В случае известной помеховой обстановки интерес представляют ДН с пониженным УБЛ в заданном угловом направлении или в секторе углов. В случае известной помеховой обстановки интерес представляют ДН с пониженным УБЛ в заданном угловом направлении или в секторе углов.

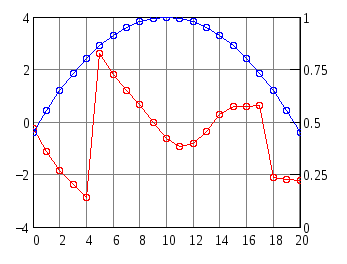
Рис. 5. Синтезированная ДН Рис. 6. Амплитудное и найденное

фазовое распределения

Рис. 7. Секторная ДН с пониженным УБЛ

дБ

Рис. 8. Найденное фазовое Рис. 9. Начальное и найденное

распределение амплитудные распределения

Итерационный метод амплитудно-фазового синтеза позволяет достаточно эффективно решать данную задачу. В таком случае необходимо дополнить условие (1):

,

где интервал углов, в котором должен быть пониженный УБЛ. На рис. 7 изображена секторная ДН с шириной главного лепестка 30° и пониженным УБЛ с одной стороны. На рис. 8 показано найденное фазовое распределение, видно, что в отличии от предыдущих случаев синтеза секторных ДН, оно стало ассиметричным. На рис. 9 представлено начальное и найденное амплитудное распределение, причем, при решении учитывалось ограничение на минимальное допустимое значение амплитуды тока в излучателе:

,

где - максимальное значение амплитуды тока среди излучателей. Антенная решетка состоит из 21 излучателя с межэлементным расстоянием 0.5λ.