
- •Санкт-Петербургский государственный электротехнический университет «лэти»
- •1.1.Основные определения и понятия. Характеристики антенн
- •2. Аксиоматика макроскопической электродинамики
- •2.1 Уравнение Максвелла, векторный потенциал, граничные условия
- •2.2.Метод самосогласованного решения антенных задач
- •3. Элементарный электрический вибратор.
- •3.1 Векторный потенциал диполя Герца.
- •3.2. Магнитное поле диполя Герца.
- •3.3. Электрическое поле диполя Герца.
- •3.4 Вектора эм поля в дальней зоне, сопротивление излучения
- •4. Линейная антенна
- •4.1. Вывод выражения для дн линейной антенны с произвольным распределением тока.
- •4.2. Дн линейной антенны с постоянным распределением тока. Соотношение неопределенности, уровень боковых лепестков.
- •5. Линейная антенная решетка
- •5.1. Вывод выражения для дн лар
- •6. Синтез афр по заданной дн.
- •6.1. Исторический обзор, особенности задач синтеза антенн.
- •6.2. Вариационный метод фазового синтеза. Примеры.
- •7. Фазовый синтез
- •7.1. Актуальность для фар, постановка задачи.
- •7.2. Итерационный метод фазового синтеза. Примеры.
- •8. Вибраторные антенны.
- •8.1. Распределение тока в вибраторной антенне на основе аналогии с длинной линией.
- •8.2. Дн симметричного вибратора.
- •8.3. Вывод уравнения Поклингтона.
- •8.3.1.Векторный потенциал цилиндрического вибратора:
- •8.3.3. Реализация граничного условия на поверхности антенны.
- •8.4. Решение уравнения Поклингтона методом Галеркина.
- •8.5. Частотная зависимость входного сопротивления симметричного вибратора.
- •9.Математическое описание вибраторных антенных решеток.
- •9.1.Система связанных иу для двухэлементной вибраторной антенной решетки с активным питанием (вывод).
- •9.2. Решение системы связанных иу
- •9.3.Система связанных интегральных уравнений для многоэлементной антенны «волновой канал».
- •9.4.Особенности системы иу для коллинеарной фар.
- •10. Краткий обзор существующих программных средств
- •10.1. Программы серии nec (winNec, miniNec, SuperNec) и другие программные средства для анализа проволочных структур.
- •10.2. 2D и 3d программные средства сапр антенн (mwo, mws, Ansoft hfss)
- •11. Заключение
- •Литература
3.2. Магнитное поле диполя Герца.
Из определения векторного потенциала
можно вычислить магнитное поле:
![]() .
Сомножитель
.
Сомножитель![]() выносится из-под знака оператораrot,
так как он не зависит от пространственных
координат, вектор
выносится из-под знака оператораrot,
так как он не зависит от пространственных
координат, вектор![]() необходимо представить в сферической
системе координат:
необходимо представить в сферической
системе координат:
1)
![]()
2)
![]() =>
=>
![]()
3)
![]()
В результате вычисление магнитного поля сводится к вычислению определителя:

Раскрывая этот определитель получим окончательное выражение для магнитного поля :

![]() =>
=>
![]() (3.2.1.)
(3.2.1.)
Выводы:
Вектор напряженности магнитного поля диполя Герца зависит только от двух координат
 иrи имеет только
азимутальную компоненту.
иrи имеет только
азимутальную компоненту.В экваториальной плоскости
 магнитное поле максимально, а в
направлениях оси вибратора
магнитное поле максимально, а в
направлениях оси вибратора отсутствует.
отсутствует.Магнитное поле имеет две составляющие, одна из которых обратно пропорциональна
 ,
а другая -
,
а другая - .
На большом расстояние от антенны
компонентой, содержащей
.
На большом расстояние от антенны
компонентой, содержащей в знаменателе, можно пренебречь.
в знаменателе, можно пренебречь.Амплитуда магнитного поля прямо пропорциональна произведению
 (моменту диполя).
(моменту диполя).
3.3. Электрическое поле диполя Герца.
Электрическое поле можно вычислить двумя способами: непосредственно из уравнений Максвелла, по известному магнитному полю, либо используя соотношение :
![]() .
(3.3.1)
.
(3.3.1)
Пусть среда распространения волн –
воздух. Тогда
![]() .
Для вычисленияdivвоспользуемся декартовой системой
координат:
.
Для вычисленияdivвоспользуемся декартовой системой
координат:![]()
![]()
![]()
Представим
![]() в сферической системе координат учитывая,
что
в сферической системе координат учитывая,
что![]() :
:
![]() .
.
Вычислим gradФ:
![]()
 .
.
Теперь, подставляя полученное выражение в формулу 3.3.1. запишем окончательно электрическое поле диполя Герца:


В полученном выражении можно выделить
две компоненты:
![]() .
.
![]()
![]()
Выводы:
Электрическое поле диполя Герца имеет радиальную (
 )
и угломестную (
)
и угломестную (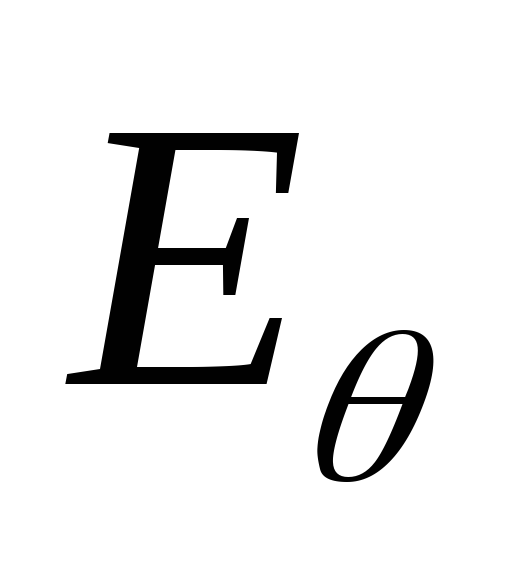 )
составляющие, причем радиальная
компонента убывает значительно быстрее
угломестной .
)
составляющие, причем радиальная
компонента убывает значительно быстрее
угломестной .В зависимости от расстояния от диполя до точки наблюдения можно сделать разделение по трем зонам: (а) ближняя, (б) промежуточная, (в) дальняя. Под ближней зоной подразумевают область, где наибольшую амплитуду имеет компонента с
 в знаменателе. В дальней зоне, где
электрическое поле имеет только
угломестную компоненту, наибольшая
амплитуда будет у компоненты с
в знаменателе. В дальней зоне, где
электрическое поле имеет только
угломестную компоненту, наибольшая
амплитуда будет у компоненты с в знаменателе.
в знаменателе.
![]()
 .
.
Теперь, учитывая, что величина
 Ом - импеданс свободного пространства,
запишем окончательное выражения для
электрического поля диполя Герца в
дальней зоне:
Ом - импеданс свободного пространства,
запишем окончательное выражения для
электрического поля диполя Герца в
дальней зоне:
![]() .
(3.3.2.)
.
(3.3.2.)
3.4 Вектора эм поля в дальней зоне, сопротивление излучения
Из соотношений 3.2.1. и 3.3.2. можно установить связь между векторами электрического и магнитного поля в дальней зоне:
![]()
Из этой формулы виден смысл импеданса свободного пространства, а сама формула представляет собой своеобразный «закон Ома» для полей.
Рассмотрим энергетические характеристики
диполя Герца и ответим на вопросы: от
чего зависит мощность излучения диполя?
Для этого окружим диполь сферой
бесконечного радиуса. Как известно,
вектор Умова-Пойнтинга равен:
![]()
![]() .
Электрическое и магнитное поле диполя
Герца в дальней зоне мы знаем, а значит,
можем получить вектор Умова-Пойнтинга,
модуль которого равен мощности
излучения, приходящейся на один
квадратный метр площади. Если
проинтегрировать вектор Умова-Пойнтинга
по всей сфере, то получим полную излученную
мощность:
.
Электрическое и магнитное поле диполя
Герца в дальней зоне мы знаем, а значит,
можем получить вектор Умова-Пойнтинга,
модуль которого равен мощности
излучения, приходящейся на один
квадратный метр площади. Если
проинтегрировать вектор Умова-Пойнтинга
по всей сфере, то получим полную излученную
мощность:
![]() ,
,
где
![]() .
.
Найдем вектор Умова-Пойнтинга:
![]() .
.
Теперь вычислим полную излученную мощность:
![]()
 .
.
Последний интеграл легко берется заменой
переменных и равен 4\3. Из данного
результата вытекает важный вывод; при
фиксированной амплитуде тока в ДГ
мощность излучения пропорциональна
квадрату отношения длины диполя к длине
волны
![]() ,
что доказывает неэффективность коротких
антенн. Последнее выражение мы можем
записать в виде:
,
что доказывает неэффективность коротких
антенн. Последнее выражение мы можем
записать в виде:![]() ,
,![]() - сопротивление излучения, т.е. коэффициент
пропорциональности между мощностью
излучения и квадратом действующего
значения тока на входных зажимах
излучателя. Очевидно, что при КПД равном
единице сопротивление излучения и
входное сопротивление антенны совпадают.
- сопротивление излучения, т.е. коэффициент
пропорциональности между мощностью
излучения и квадратом действующего
значения тока на входных зажимах
излучателя. Очевидно, что при КПД равном
единице сопротивление излучения и
входное сопротивление антенны совпадают.
