5.3. Обобщение на антенны с произвольно поляризованным излучением

В

Рис. 5.5

общем случае поле излучения антенны имеет вертикальную и горизонтальную составляющие, причем каждая из них обладает своей характеристикой направленности. Полное поле каждой из антенн представляется как сумма вертикальной и горизонтальной составляющих. Запишем поле антенны 1 в произвольной точкеМ1-го полупространства (рис. 5.5). Для этого сложим выражения (5.2) и (5.5), подставляя в них координаты точкиМ:

. (5.9)

В той же точке Мполе зеркального изображения равно

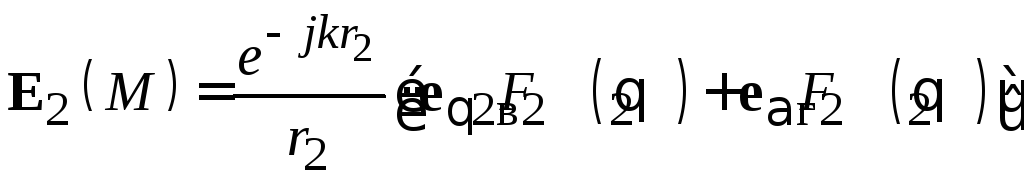. (5.10)

Если точка наблюдения находится в дальней зоне системы «антенна 1 антенна 2», то выполняются неравенства>>,>>,>>. В этом случае выражения (5.9) и (5.10) можно упростить. При выполнении указанных неравенств лучи О₁Ми О₂Мпрактически параллельны; поэтому. Кроме того, в знаменателях (5.9) и (5.10) можно положить. Тогда

, (5.11)

. (5.12)

Наконец, примем, что характеристики направленности и по горизонтальной, и по вертикальной составляющим симметричны относительно . Тогда действуют связи (5.4) и (5.8). Учитывая их, преобразуем (5.12):

. (5.13)

Следует отметить, что поля антенн 1 и 2 из-за разницы знака при в (5.11) и (5.13) поляризованы неодинаково. Допустим, например, чтоиравны по модулю и сдвинуты по фазе на 90º, так что квадратную скобку в (5.11) можно записать в виде. Это означает, что поле антенны 1 имеет левую круговую поляризацию (если смотреть по направлению распространения волны). В то же время для поля антенны 2 та же скобка записывается как, т. е. это поле с правой круговой поляризацией.

5.4. Интерференция полей антенны и ее зеркального изображения

Складывая выражения (5.11) и (5.13), получим

. (5.14)

В

Рис. 5.6

выражении (5.14) следует учесть, что расстоянияив дальней зоне из-за параллельности лучей О₁Ми О₂М(рис. 5.5) могут быть представлены в видеДалее вместо угла места сферической системы координатбу­дет использоваться угол возвышения(рис. 5.6). Тогда получим

. (5.15)

В этом случае

,

. (5.16)

С учетом (5.14) и (5.16) окончательное выражение для поля в точке Мпримет вид

(5.17)

Векторная функция в квадратных скобках (5.17) называется характеристикой направленности антенны, поднятой над идеально проводящей поверхностью. Заметим сразу, что проводящая плоскость может существенно изменить поляризационные свойства поля антенны. Пусть, например, , т. е. поле антенны 1 имеет круговую поляризацию. Тогда выражение для суммарного поля излучения поля в точке наблюденияМ(см. рис. 5.5) примет вид:

.

Как видно, -я и-я компоненты полянаходятся либо в фазе (при одинаковых знаках обеих компонент), либо в противофазе (при противоположных знаках). В обоих случаях это линейная поляризация. При этом с изменением угласоотношение-й и-й компонент изменяется, так что изменяется и ориентация линейно поляризованного вектора электрического поля.

5.5. Частные случаи

Вертикальный диполь Герца создает, как известно, вертикально поляризованное электрическое поле.

Рис. 5.7

При этом (рис. 5.7,а), так что диаграмма направленности диполя над проводящей поверхностью:

. (5.18)

Такой же диполь, расположенный горизонтально (рис. 5.7, б), в плоскости, проходящей через центр диполя перпендикулярно его моменту, создает горизонтально поляризованное поле, причем ДН не зависит от угла. Следовательно,

. (5.19)

Для полуволнового вибратора, при его вертикальной ориентации, учитывая (5.18), получим

.

Для горизонтального вибратора , так что выражение длясовпадает с (5.19).