Самостоятельная работа №3 "Построение и исследование адаптивной системы с параметрической настройкой для двухмассового упругого электромеханического объекта третьего порядка"

Целью выполнения данной работы является:

• овладение навыками исследования адаптивной системы;

• исследование эффективности адаптивного управления при изменении параметров объекта;

• исследование возможностей адаптивного управления по стабилизации объекта управления;

Для выполнения задания по самостоятельной работе достаточно внимательно изучить методику построения и расчета прямых адаптивно-модальных систем автоматического управления с параметрической настройкой, изложенную в главе 7 лекций по дисциплине "Методы проектирования систем управления многостепенными механическими объектами с упругими деформациями", и, ледуя материалу главы 7 и настоящим указаниям, выполнить расчет адаптивно-модальной системы, приняв следующие параметры линеаризованного упругого двухмассового объекта, замкнутого по первой скорости [уравнения (7.6), (7.7), (7.8)]:

Таблица вариантов заданий по самостоятельной работе

Параметр	№ варианта
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
	0,1	0,2	0,3	0,4	0,5	1,0	1,0	1,0	0,1	0,1	0,1	0,2	0,3	0,4	0,5	0,05	0,1	0,2	0,3	0,4
	25	25	25	50	50	100	250	75	75	50	10	50	75	100	125	25	100	100	100	50

Каждому студенту в каждой группе необходимо выбрать из таблицы вариантов вариант с номером, соответствующим номеру, под которым он числится в списке своей группы

Расчет выполнить в следующей последовательности, принятой в главе 7.

1. В качестве двухмассового упругого электромеханического объекта принять двухконтурную следящую систему. Ее линеаризованные уравнения (без учета упругости) имеют вид (7.1), причем в них, пренебрегая электромагнитной постоянной инерцией обмотки статора двигателя, примем . Расчет настроек контурных регуляторов следящей системы выполнить по следующими формулам (все не раскрытые здесь обозначения пояснены в главе 7). Формулы настроек подчиненных контуров следующие:

для П-регулятора скорости:

; ;

для П-регулятора положения:

.

Приведенные расчетные формулы для контурных регуляторов скорости и положения приведены без учета упругих свойств объекта. Если учесть упругость уравнениями (7.2 а,б), то такие настройки при пренебрежении зазора ( и ) вызовут слабозатухающие или незатухающие колебания в системе, изображенной на рис. 7.1, в чем легко убедится моделированием. В то же время моделированием также легко проверить, что в "жесткой" системе (7.1) указанные настройки обеспечат удовлетворительное качество переходных процессов, свойственное правильно настроенной жесткой электромеханической следящей системе с подчиненным управлением.

2. Записать линейное стационарное приближение (7.6) уравнений (7.2 а, б) с упругим электромеханическим объектом с параметрами, соответствующими выбранному из таблицы варианту, вычислить коэффициенты, данные соотношениями (7.7), и записать в числовом виде систему (7.8).

3. Коэффициенты обратных связей модального регулятора (7.9) рассчитать в соответствии с методикой, описанной в п. 7.3. главы 7. Значение в уравнениях (7.15) принять равным .

4. Расчет идентификатора состояния (наблюдателя) выполнить согласно методики, изложенной в п. 7.4 главы 7, при этом значение множителя q в желаемом характеристическом многочлене (7.20) наблюдателя принять равным q=2.

5. Расчет адаптивного управления с параметрической настройкой осуществляется согласно п. 7.7 главы 7. При этом в уравнениях (7.32) огрублением пренебрегают и первоначальные значения параметров принимаются следующие: , , , .

6. Исследование моделированием построенной адаптивной системы является важным этапом ее отладки, так как только в процессе отладки могут быть уточнены значения коэффициентов параметрической настройки.

В процессе моделирования исследуются переходные реакции переменных и линеаризованного упругого объекта (7.6)÷(7.8) на ступенчатое входное воздействие при следующих условиях (влиянием зазора принебрегаем):

1. при усредненных параметрах упругого объекта , , 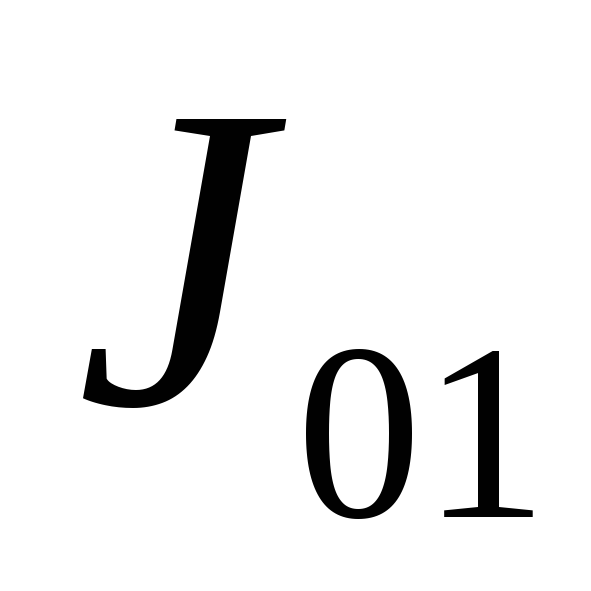с подчиненным управлением , ;

2. при усредненных параметрах упругого объекта с модальным управлением и наблюдателем;

3. при изменении параметров упругого объекта с модальным управлением и наблюдателем в диапазонах: , , , , , 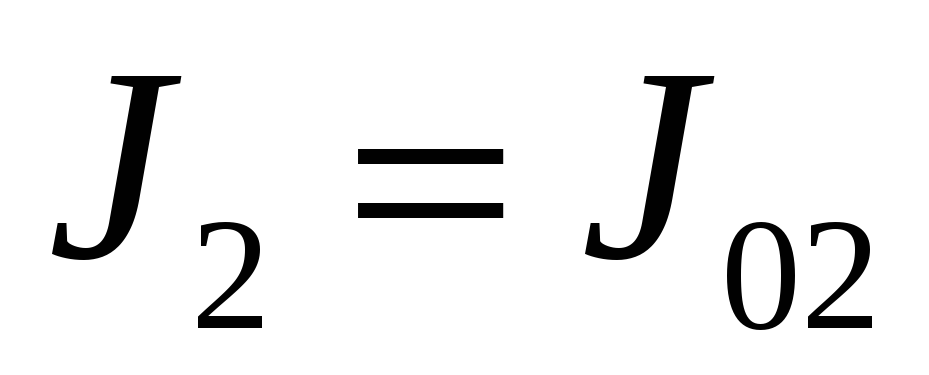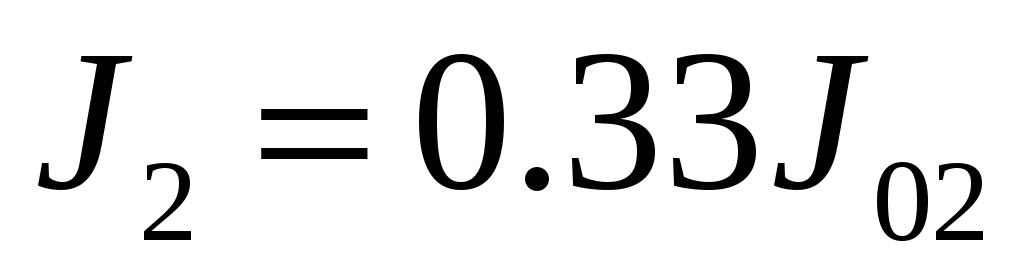(рассмотреть все сочетания);

4. при усредненных параметрах упругого объекта с адаптивно-модальным управлением;

5. при усредненных параметрах упругого объекта с адаптивно-модальным управлением при изменении параметров ;

6. для лучших параметрах , с точки зрения динамики переходного процесса, упругого объекта с адаптивно-модальным управлением при изменении параметров в диапазонах: , , , , , (рассмотреть все сочетания).

7. Результаты самостоятельной работы оформить в виде сброшюрованного научно-технического отчета и сдать экзаменатору при получении экзаменационного билета.

Пример выполнения работы.

Дано:

, , , , , , , ,

РАСЧЕТ МОДАЛЬНОЙ ЭЛЕКТРОМЕХАНИЧЕСКОЙ СЛЕДЯЩЕЙ СИСТЕМЫ С ДВУХМАССОВЫМ УПРУГИМ МЕХАНИЧЕСКИМ ОБЪЕКТОМ И НАБЛЮДАТЕЛЕМ

Расчет замкнутого контура скорости с двухмассовым упругим электромеханическим объектом и подчиненным управлением

Примем в качестве исходного двухмассовый упругий электромеханический объект с зазором, замкнутый по скорости с контурным П-регулятором и являющийся внутренним контуром двухконтурной электромеханической системы (см. рисунок 1). Его дифференциальные уравнения имеют вид:

(1)

где – упругий момент, возникающий при деформации в упругой связи при отсутствии зазора; – упругий момент, описываемый при учете зазора 2 в упругой связи нелинейной (недифференцируемой) функцией вида

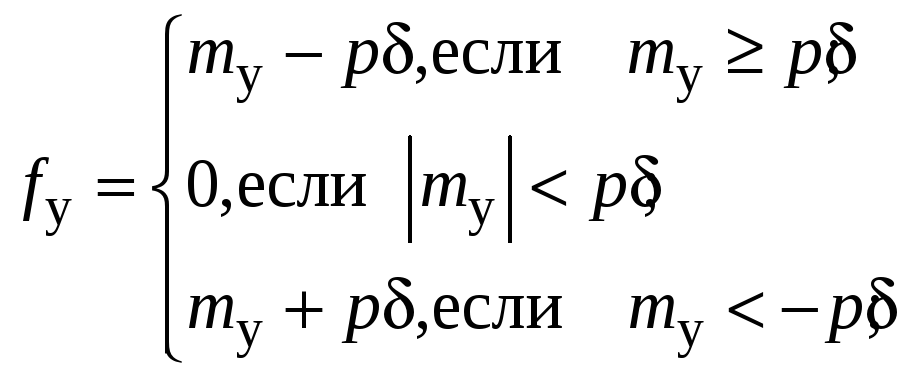(2)

– соответственно, момент инерции двигателя и момент инерции механизма нагрузки с учетом его приведения к вращению двигателя; p – коэффициент упругости (жесткости упругой связи); – соответственно, угловые скорости первого и второго дисков ; – настраиваемый коэффициент контурного П-регулятора скорости (); – известное программное (задающее) воздействие (для внутреннего контура скорости это выходной сигнал регулятора РП); и – соответственно, линейное и адаптивное управления, подлежащие определению.

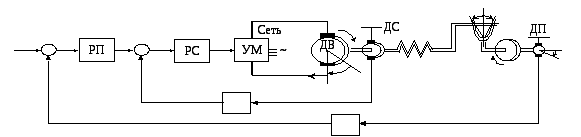
Рисунок 1 - Двухмассовый нелинейный упругий электромеханический объект с подчиненным управлением

Таким образом, описание контура скорости электромеханической следящей системы с двухмассовым упругим механическим объектом исчерпывается (с учетом принятых ранее допущений) системой нелинейных дифференциальных уравнений (1), (2) третьего порядка, записанных в так называемой скоростной форме уравнений упругого объекта. Кроме того, считаем, что в общем случае моменты инерции, отнесенные к двигателю и нагрузке, а также коэффициент жесткости являются неизвестными и нестационарными (функциями времени):

, (3)

Рисунок 2 - Детализированная структурная схема замкнутого по первой скорости двухмассового упругого электромеханического объекта с зазором в упругой связи (1), (2)

Замечание. В дальнейших исследованиях будем пренебрегать нелинейностью и нестационарностью уравнений (1)÷(3) исходного упругого объекта (1)÷(3) и будем рассматривать его линейное и стационарное приближение с некоторыми усредненными постоянными параметрами:

. (5)

С учетом обозначений (5) и пренебрегая в уравнениях (1), (2) зазором ( и ) запишем линейное стационарное приближение контура скорости с упругим механическим объектом в виде:

(6)

Введем следующие обозначения:

(7)

С учетом введенных обозначений перепишем линеаризованные уравнения (6) с усредненными параметрами (7) в компактной форме

и для удобства представим их в векторно-матричной записи:

(8)

где – вектор состояния линеаризованного объекта (6); – уравнение измерения; (здесь доступной измерению с помощью датчика скорости ДС считается первая скорость ).

Примем дифференциальную линейную систему (8) с параметрами (7) в качестве исходного расчетного объекта управления.

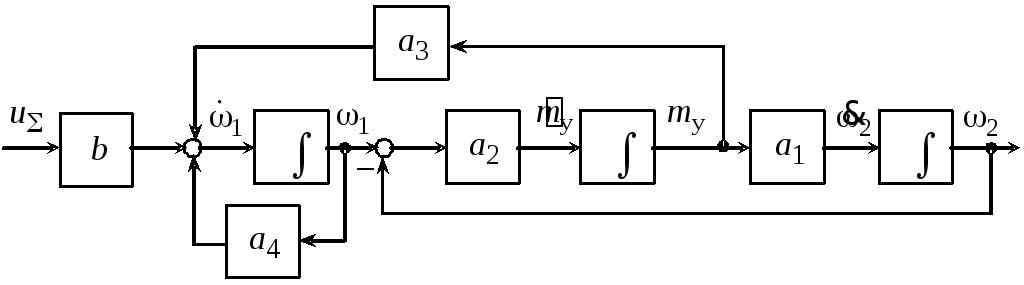
Рисунок 3 - Детализированная структурная схема замкнутого по первой скорости линеаризованного двухмассового упругого электромеханического объекта (6)–(8)

Числовой расчет объекта управления выполним по формулам (7), приняв следующие числовые значения параметров (см. задание):

кгм²; кгм²;

Нм/рад; Ом;

Вс; Вс;

; Вс/рад;

В/рад; рад/с;

= 0,35 (кгм²); рад/с;

; .

Расчет контурных регуляторов , выполним по формулам подчиненного управления, справедливым для жесткого объекта (при пренебрежении упругой связью, когда - велико, или :

; .

Получаем:

• значения контурных регуляторов , :

;

;

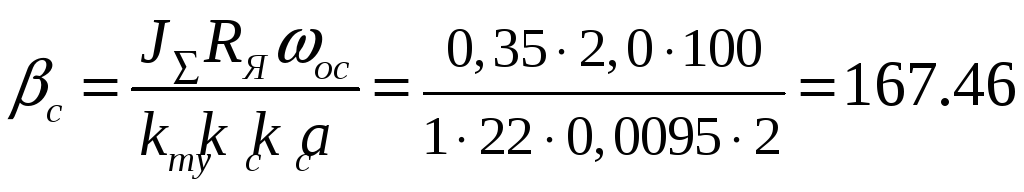• значения параметров (7) дифференциальной линейной системы (8):

Запишем дифференциальную линейную систему (8) в численном виде:

Сначала построим объект (6), (7) без учета упругих свойств, упрощая их и получая систему уравнений трехконтурной следящей системы с жестким объектом вида:

Далее построим и проведем исследования двухконтурной следящей системы с жестким объектом, принимая в ней , , :

Получим переходный процесс вида (см. рисунок 4). На рисунке 5 представлен график переходного процесса в двухконтурной следящей системе с жестким объектом и подчиненным регулированием.

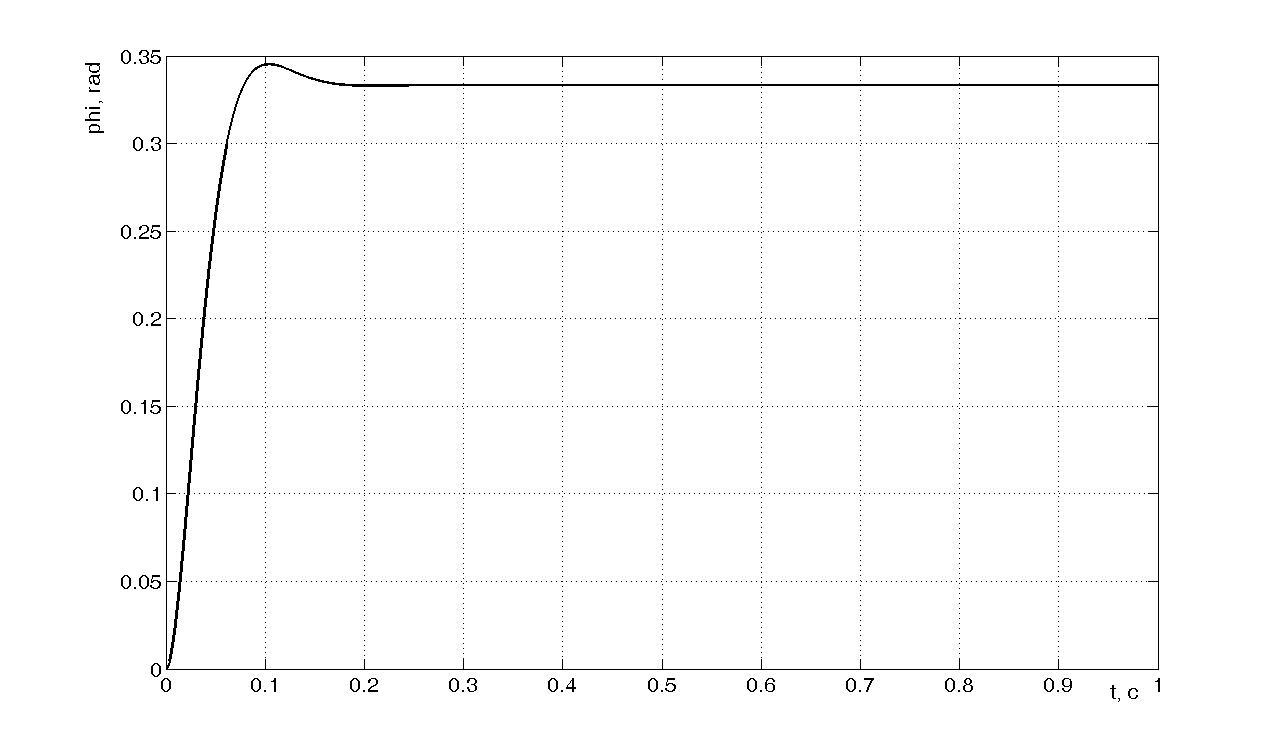
Рисунок 4 - Переходный процесс в двухконтурной следящей системе с жестким объектом и подчиненным регулированием.

а б

Рисунок 5 - Переходный процесс в системе с двухмассовым упругим объектом с подчиненным регулированием: а) при , ; б) при , .