
Самостоятельная 1
.docСамостоятельная работа №1
"Построение и исследование адаптивной системы с параметрической настройкой для объекта первого порядка"
Целью выполнения данной работы является:
-
овладение навыками исследования адаптивной системы;
-
исследование эффективности адаптивного управления при изменении параметров уравнений его настроек;
-
исследование возможностей адаптивного управления по стабилизации объекта управления.
Исследование объекта первого порядка, заданного апериодическим звеном.
Рассмотрим объект управления, заданный апериодическим звеном первого порядка, описываемый уравнением:
![]() ,
,
![]() (1)
(1)
где
![]() - неизвестные вещественные числа;
- неизвестные вещественные числа;
![]() - скалярные вещественные функции;
- скалярные вещественные функции;
![]() - программное управление, а
- программное управление, а
![]() - адаптивное управление, подлежащее
определению.
- адаптивное управление, подлежащее
определению.
Эталонная модель описывается уравнением:
![]() (2)
(2)
Закон адаптивного управления с параметрической настройкой (без огрубления) имеет вид
![]() (3)
(3)
где
![]() ,
,
![]() - настраиваемые параметры закона
управления описываются следующими
дифференциальными уравнениями:
- настраиваемые параметры закона
управления описываются следующими
дифференциальными уравнениями:
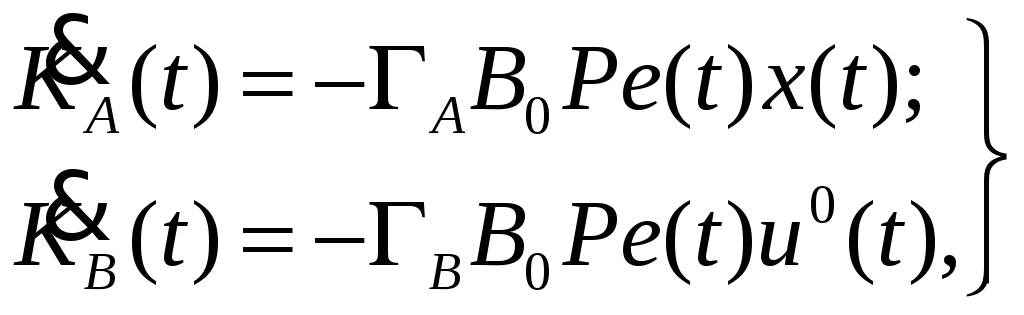 (4)
(4)
![]() –
положительные
коэффициенты усилений настроек;
–
положительные
коэффициенты усилений настроек;
![]() разность между переменными состояния
объекта (1) и эталонной модели (2).
разность между переменными состояния
объекта (1) и эталонной модели (2).
На рисунке 1 изображена структурная схема построенной адаптивной системы (1)÷(4).
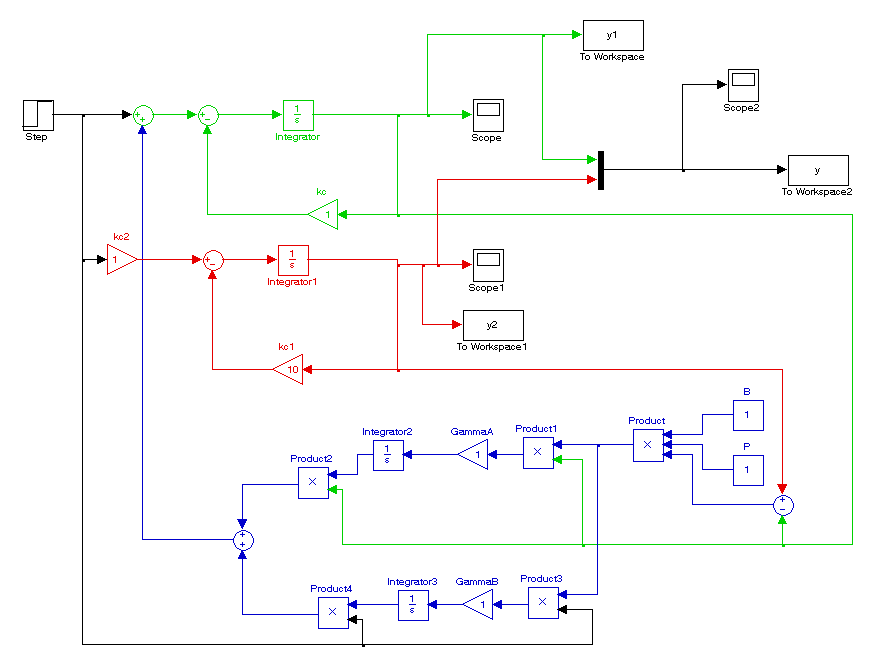
Рисунок 1 - Структурная схема адаптивной системы управления
Задание:
-
Построить и исследовать моделированием систему (1) с заданными параметрами
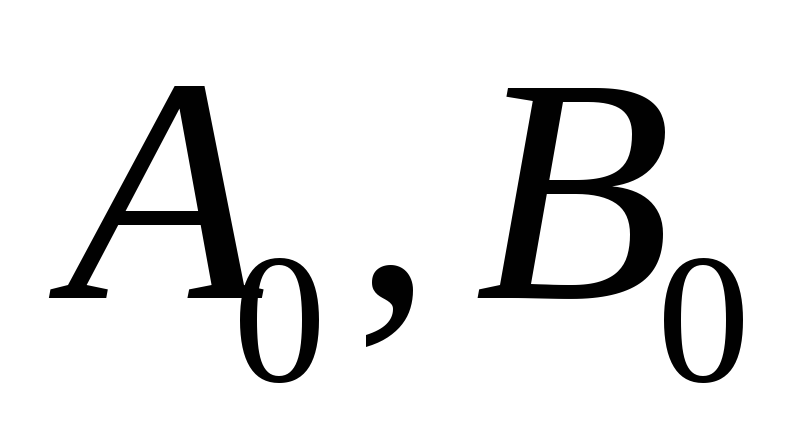 для устойчивого случая (
для устойчивого случая (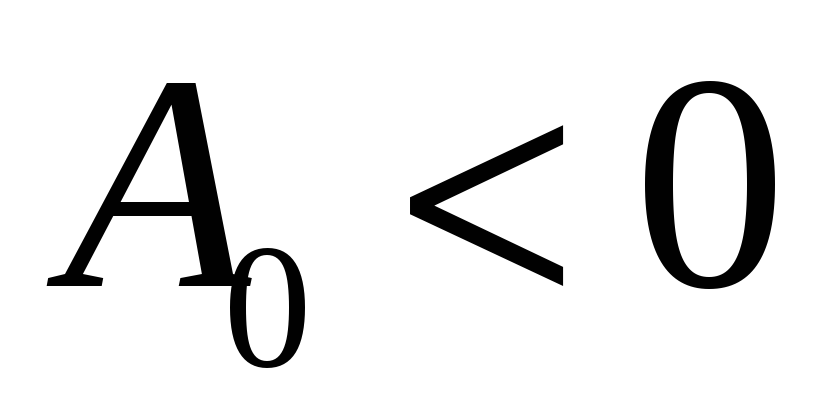 ).
). -
Построить эталонную модель (2) и сравнить ее динамику с динамикой объекта управления (1).
-
Построить адаптивное управление (3) с настройками (4) и начальными значениями
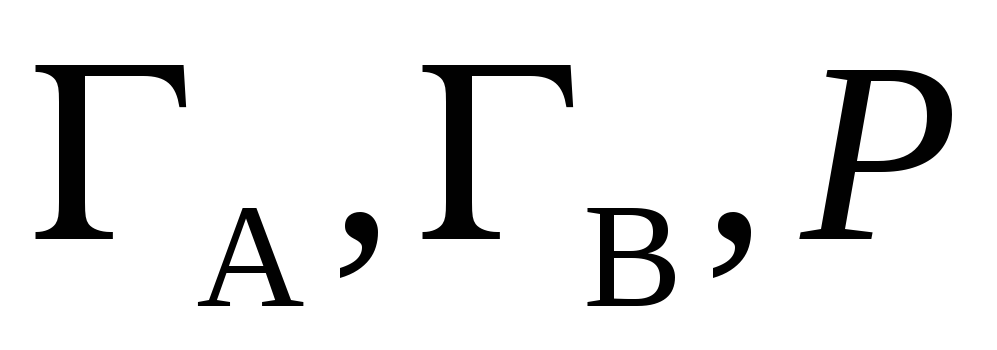 по своему варианту.
по своему варианту. -
Исследовать адаптивную систему, изменяя коэффициенты
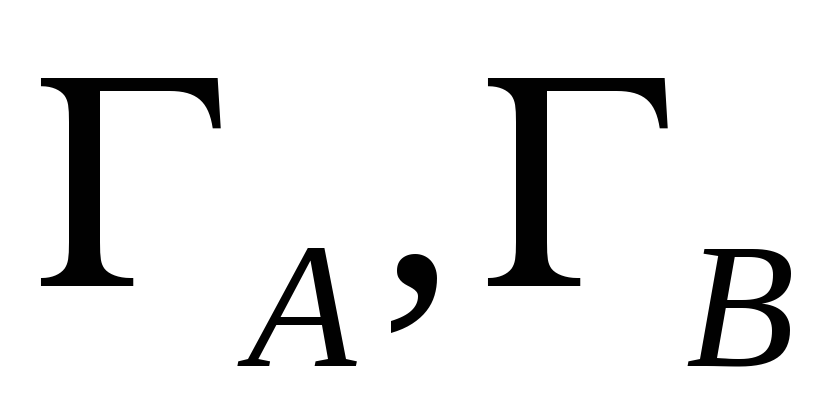 (
(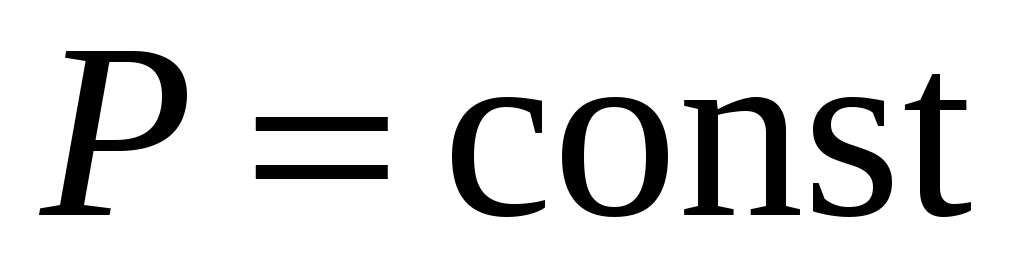 ).
).
-
Записывать установившиеся значения для
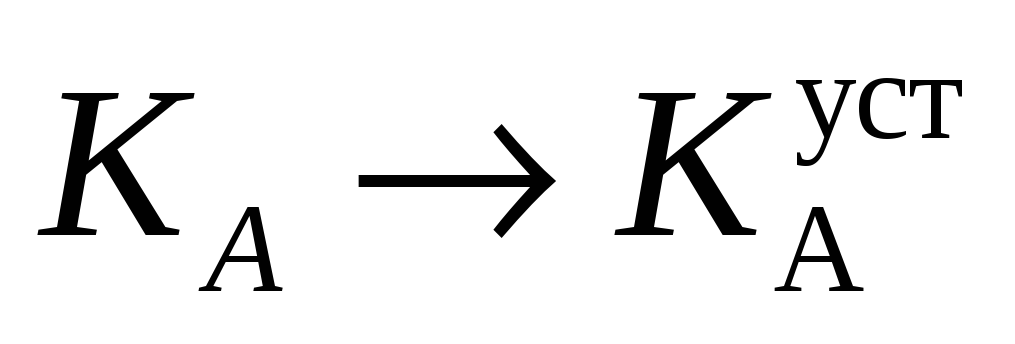 и
и
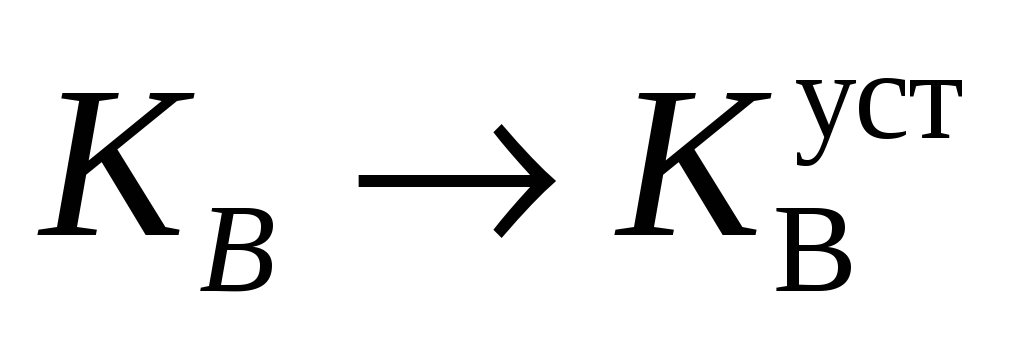 и сравнивать их со значениями, полученными
из формул
и сравнивать их со значениями, полученными
из формул
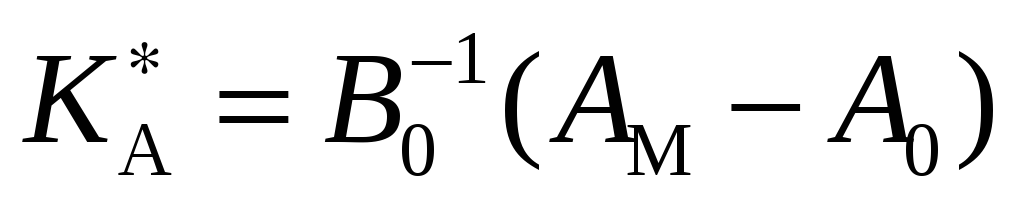 ,
,
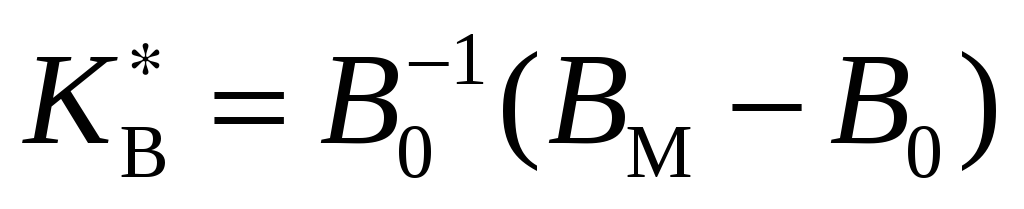 .
. -
Сделать выводы о работе адаптивной системы с параметрической настройкой для управления устойчивым объектом.
-
Построить и исследовать моделированием объект (1) с заданными параметрами
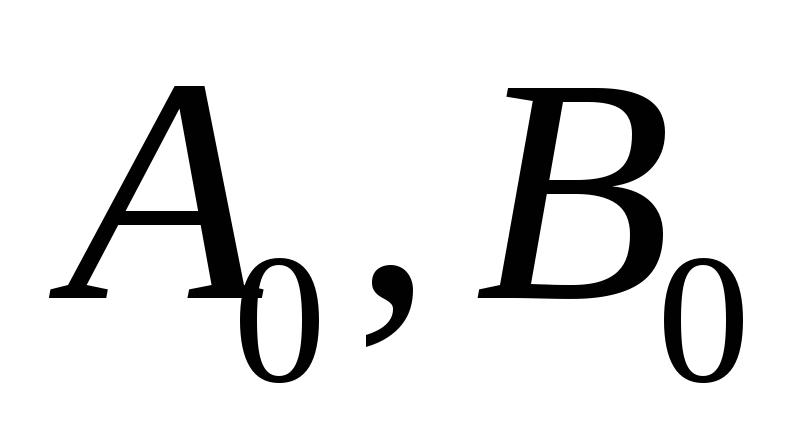 для неустойчивого случая (
для неустойчивого случая (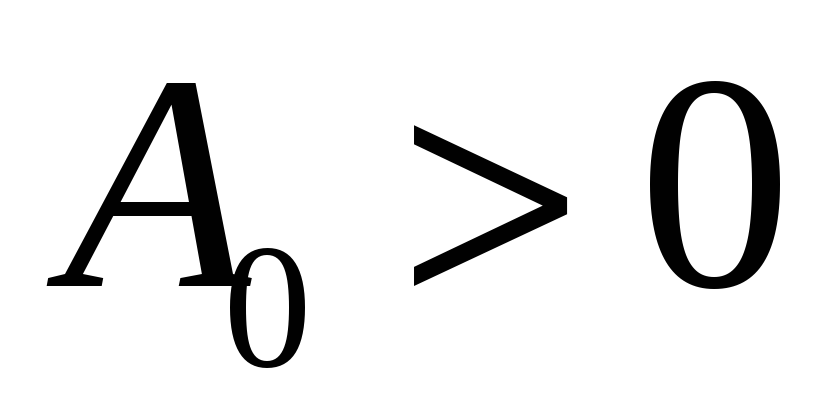 ).
). -
Повторить п.3-6 для случая неустойчивого объекта.
Пример выполнения работы
Исследование объекта первого порядка, заданного апериодическим звеном.
Устойчивый объект
Дано:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Рассмотрим объект первого порядка, описываемый уравнением
![]() ,
,
![]() (1)
(1)
Структурная схема объекта показана на рисунке 1.
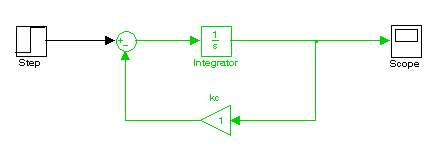
Рисунок 1 - Структурная схема объекта первого порядка
Построим
и исследуем объект с
![]() и получим переходный процесс вида (см.
рисунок 2), имеющий время регулирования
и получим переходный процесс вида (см.
рисунок 2), имеющий время регулирования
![]() .
.
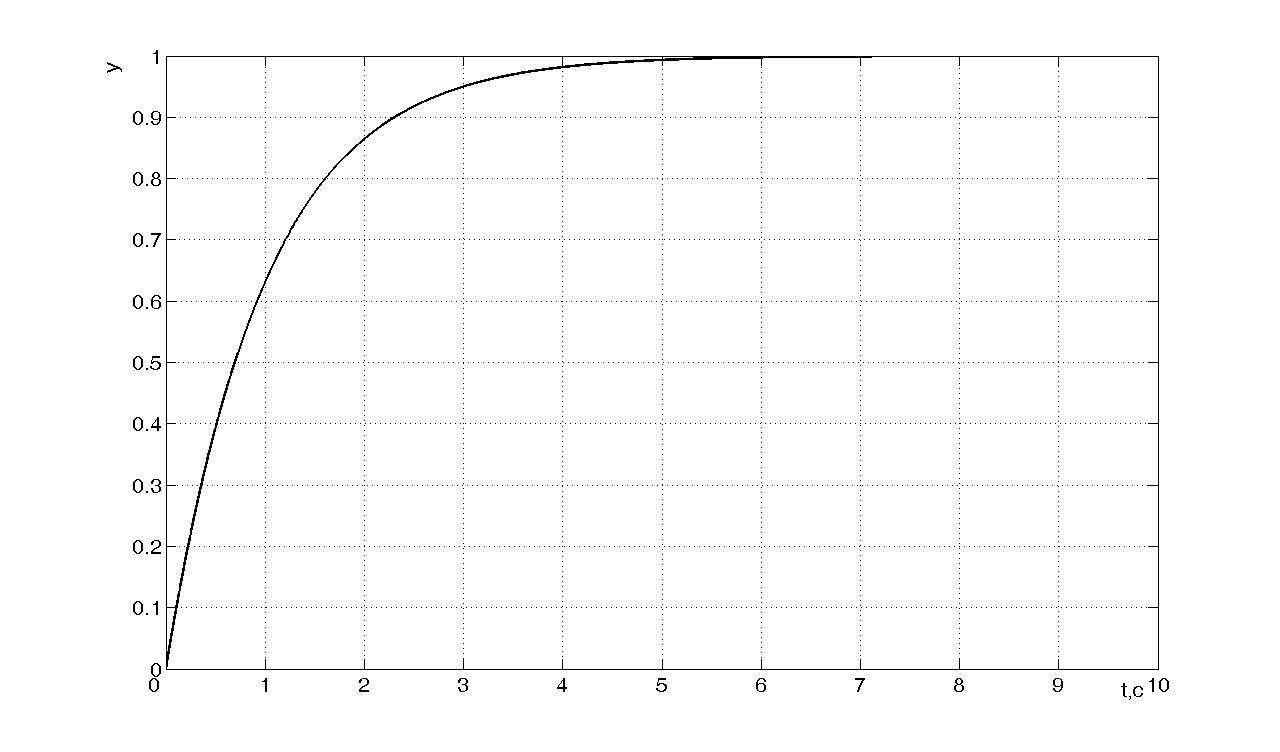
Рисунок 2 - Переходный
процесс в объекте первого порядка при
![]() .
.
Построим адаптивное управление объектом (1), задавая желаемые переходные процессы объекта с адаптивным управлением с помощью эталонной модели:
![]() .
(2)
.
(2)
Задавая
![]() ,
сравним траектории эталонной модели
(см. рисунок 3,
,
сравним траектории эталонной модели
(см. рисунок 3,
![]() )
и самого объекта управления.
)
и самого объекта управления.
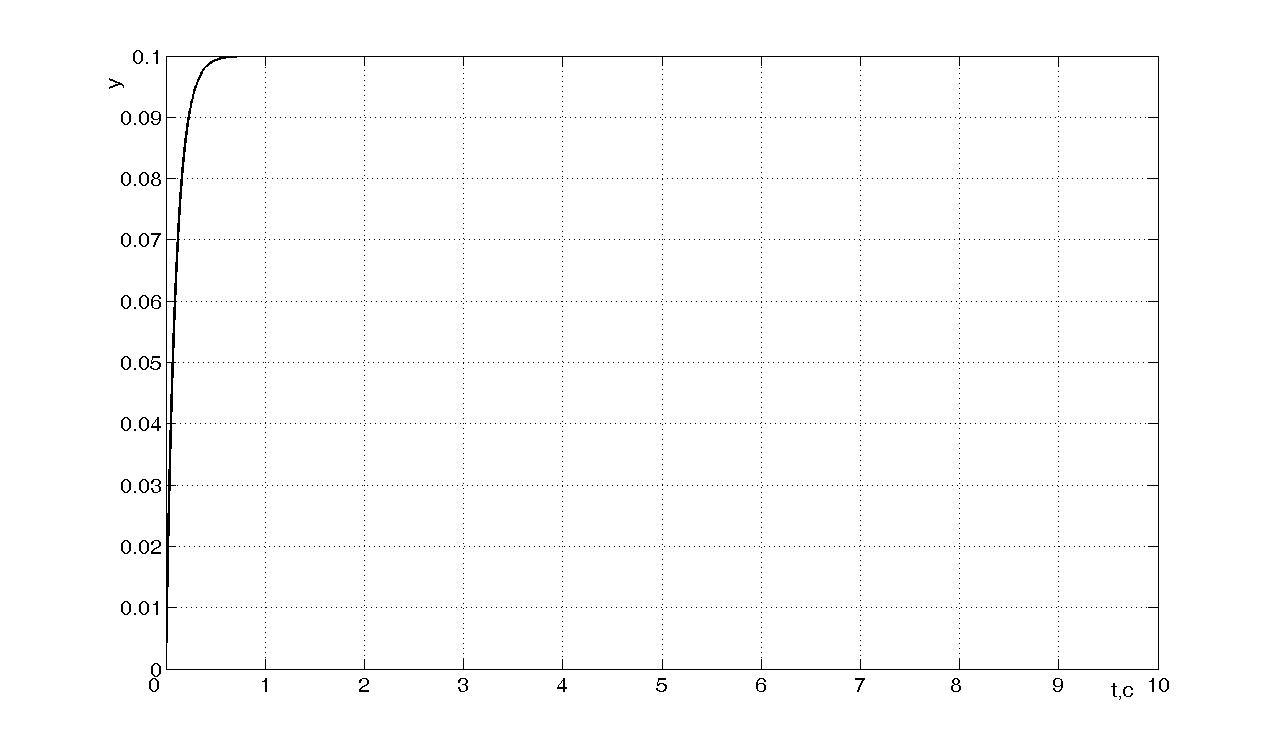
Рисунок 3 - Переходный
процесс в эталонном объекте первого
порядка при
![]() .
.
Как видно, у эталонной модели время переходного процесса и заданное установившееся значение в 10 раз меньше, чем у объекта.
Построим систему адаптивного управления с параметрической настройкой (без огрубления).
![]() ;
(3)
;
(3)
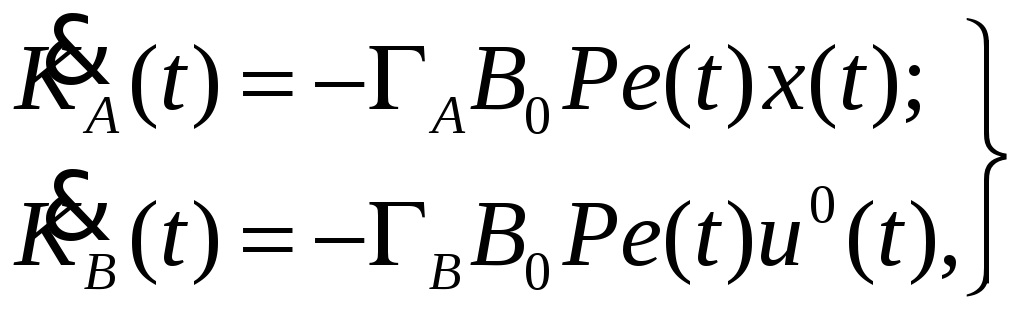 (4)
(4)
где
![]() ,
,![]() – настраиваемые коэффициенты адаптивного
закона;
– настраиваемые коэффициенты адаптивного
закона;
![]() – положительные коэффициенты усилений
настроек;
– положительные коэффициенты усилений
настроек;
![]() – ошибка – разность между переменными
состояния объекта (1) и эталонной модели
(2).
– ошибка – разность между переменными
состояния объекта (1) и эталонной модели
(2).
Проведем исследование адаптивной системы (1)÷(4) при следующих параметрах:
1)![]() ,
,
![]() ,
,
![]() ,
,
![]() $
$
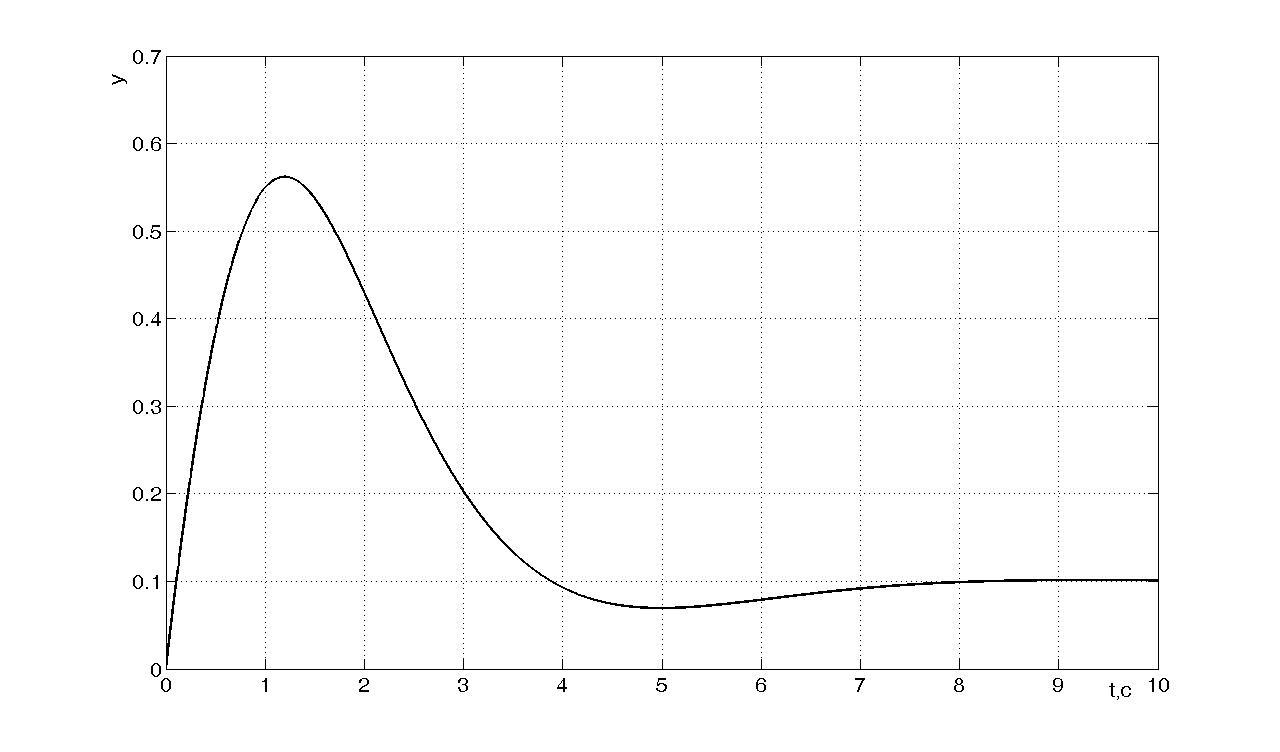
Рисунок 4 - Переходный
процесс при
![]()
.
.
.
n)
![]() ,
,
![]() ,
Р=1,
,
Р=1,
![]()
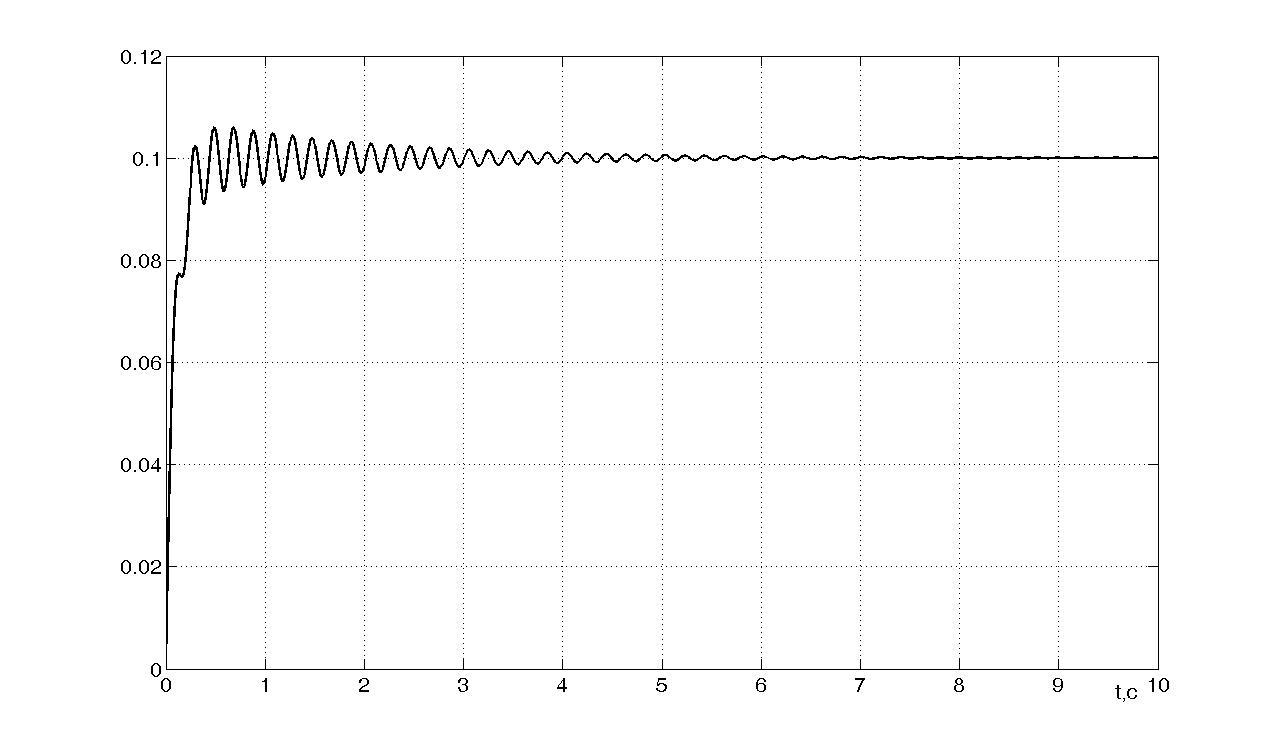
Рисунок n
- Переходный процесс при
![]()
Для
системы
![]() ,
,
![]() ,
,
![]() ,
,
![]() установившиеся значения настроек
установившиеся значения настроек
![]() и
и
![]() по графикам переходных процессов будут:
по графикам переходных процессов будут:
![]() ,
,
![]() .
Расчетные значения:
.
Расчетные значения:
![]() ,
,
![]() .
.
Рассмотрев
переходные процессы, делаем вывод о
том, что в устойчивом объекте можно
добиться желаемого быстродействия,
вводя адаптивное управление с
параметрической настройкой. При этом,
чем больше коэффициенты усиления
![]() ,
тем выше колебания, возникающие в системе
и меньше перерегулирование, наконец,
при значениях
,
тем выше колебания, возникающие в системе
и меньше перерегулирование, наконец,
при значениях
![]() больше 10000 наступает момент, когда
траектории эталонной модели и объекта
управления совпадают, а это значит, что
больше 10000 наступает момент, когда
траектории эталонной модели и объекта
управления совпадают, а это значит, что
![]() и
и
![]() (в чем легко убедится, посмотрев
установившиеся значения на выходах
настроек адаптивного управления
регулятора).
(в чем легко убедится, посмотрев
установившиеся значения на выходах
настроек адаптивного управления
регулятора).
ЗАМЕЧАНИЕ.
При равенстве
![]() дифференциальное уравнение настроек
для коэффициента
дифференциальное уравнение настроек
для коэффициента
![]() можно исключить из рассмотрения
адаптивной системы (1)÷(4).
можно исключить из рассмотрения
адаптивной системы (1)÷(4).
Моделирование системы с неустойчивым объектом
Дано:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
В
предыдущем пункте мы проводили
исследования устойчивого объекта, но
обладающего динамикой в 10 раз более
медленной, чем динамика эталонной
модели. Усложним задачу адаптивного
управления, рассматривая неустойчивый
объект управления (![]() ),
и для него проведем исследование
адаптивного управления.
),
и для него проведем исследование
адаптивного управления.
Исследуем
объект с
![]() и получим переходный процесс вида (см.
рисунок n+1)
:
и получим переходный процесс вида (см.
рисунок n+1)
:
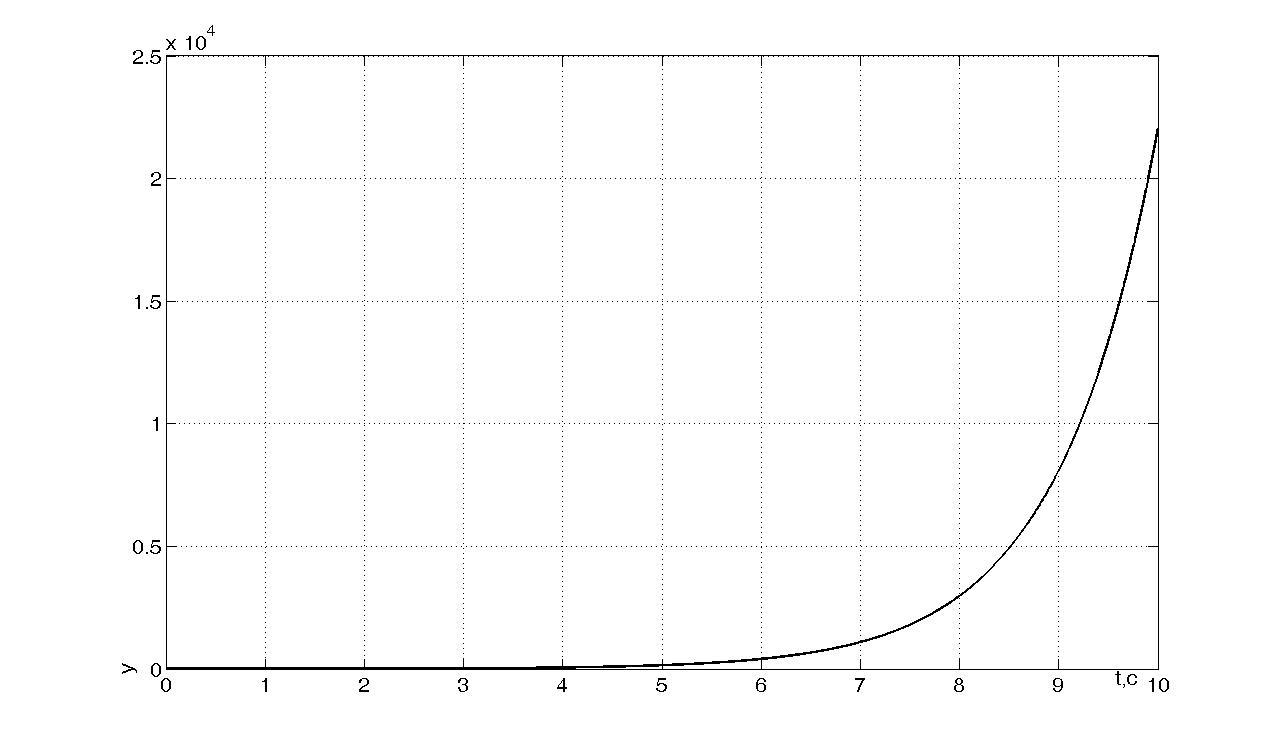
Рисунок n+1
- Переходный процесс при
![]()
Проведем исследования адаптивной системы (1)÷(4) при следующих параметрах:
1)![]() ,
,
![]() ,
Р=1,
,
Р=1,
![]()
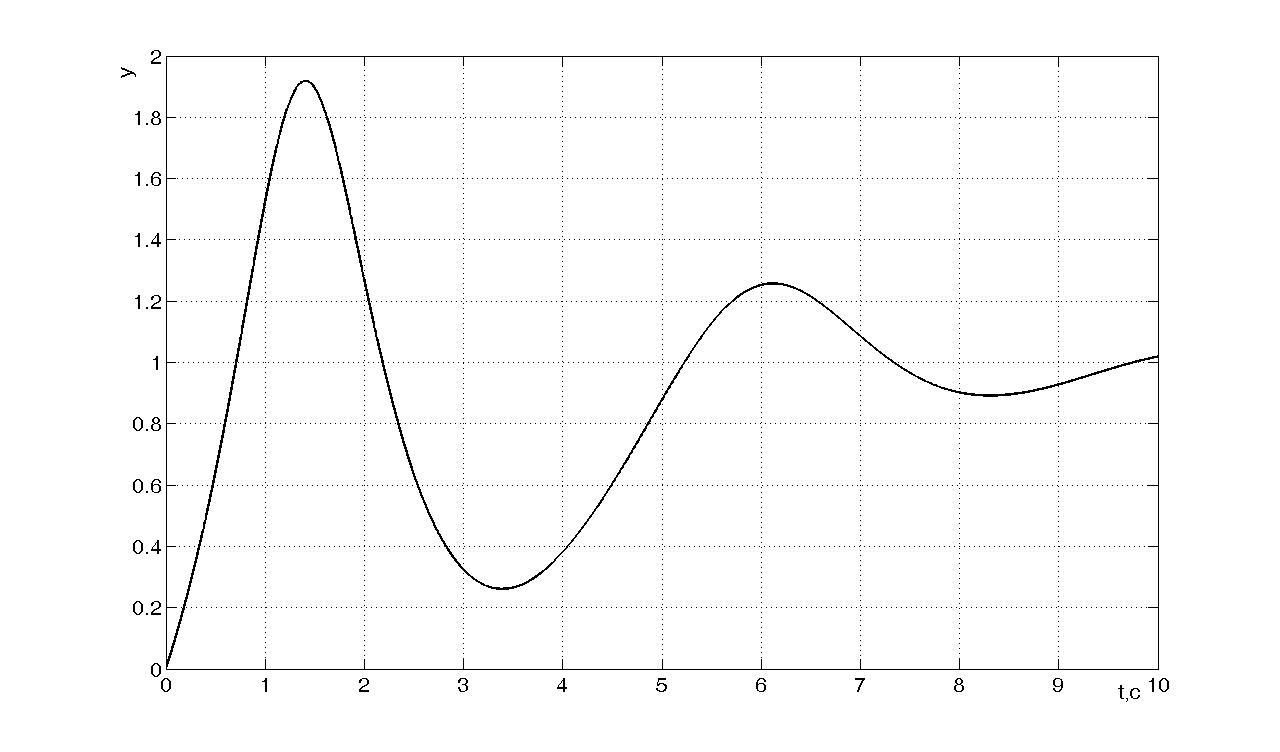
Рисунок n+2
- Переходный процесс при
![]()
.
.
.
m)![]() ,
,
![]() ,
Р=1,
,
Р=1,
![]()
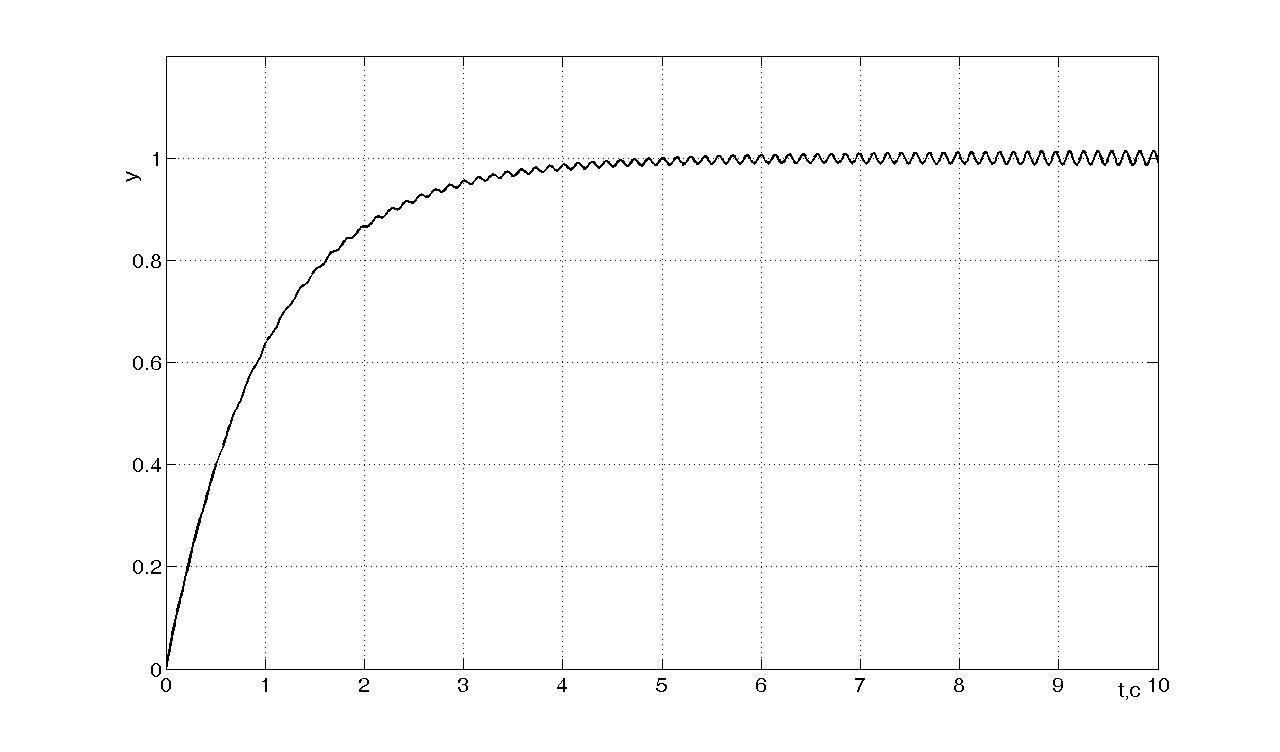
Рисунок m
- Переходный процесс при
![]()
Для
системы
![]() ,
,
![]() ,
,
![]() ,
,
![]() установившиеся значения настроек по
графикам переходных процессов будут:
установившиеся значения настроек по
графикам переходных процессов будут:
![]() ,
,
![]() .
Расчетные значения:
.
Расчетные значения:
![]() ,
,
![]() .
.
Исследование
показывает, что адаптивное управление,
как и в случае с устойчивым объектом,
справляется с задачей стабилизации
объекта управления и, как было описано
выше, чем выше коэффициенты усиления
![]() ,
тем сильнее влияние адаптивного
управления на объект, выше частота
колебаний переходного процесса и меньше
перерегулирование. При достаточно
больших коэффициентах усиления
,
тем сильнее влияние адаптивного
управления на объект, выше частота
колебаний переходного процесса и меньше
перерегулирование. При достаточно
больших коэффициентах усиления
![]() переходный процесс адаптивной системы
с совпадает с переходным процессом
эталонной модели.
переходный процесс адаптивной системы
с совпадает с переходным процессом
эталонной модели.
Варианты заданий.
Вариант №1
Первый порядок
Устойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Неустойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Вариант №2
Первый порядок
Устойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Неустойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Вариант №3
Первый порядок
Устойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Неустойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Вариант №4
Первый порядок
Устойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Неустойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Вариант №5
Первый порядок
Устойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Неустойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Вариант №6
Первый порядок
Устойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Неустойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Вариант №7
Первый порядок
Устойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Неустойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Вариант №8
Первый порядок
Устойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Неустойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Вариант №9
Первый порядок
Устойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Неустойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Вариант №10
Первый порядок
Устойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Неустойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Вариант №11
Первый порядок
Устойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Неустойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Вариант №12
Первый порядок
Устойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Неустойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
