
Самостоятельная 2
.docСамостоятельная работа №2
"Построение и исследование адаптивной системы с параметрической настройкой для объекта второго порядка"
Целью выполнения данной работы является:
-
овладение навыками исследования адаптивной системы;
-
исследование эффективности адаптивного управления при изменении параметров уравнений его настроек;
-
исследование возможностей адаптивного управления по стабилизации объекта управления.
Исследования объекта второго порядка
Рассмотрим объект управления описываемый уравнением:
![]() ,
,
![]() ,
(1)
,
(1)
где
 ,
,
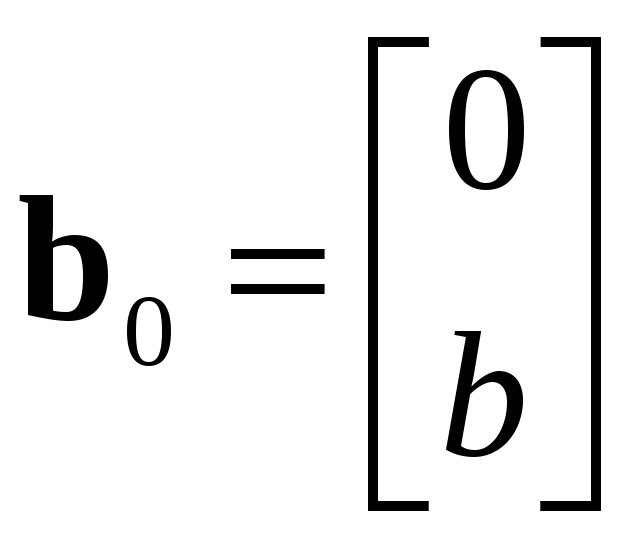 - неизвестные постоянные матрицы;
- неизвестные постоянные матрицы;
 - вектор переменных состояния;
- вектор переменных состояния;
![]() -
скалярная вещественная функция;
-
скалярная вещественная функция;
![]() - программное управление, а
- программное управление, а
![]() - адаптивное управление, подлежащее
определению.
- адаптивное управление, подлежащее
определению.
Эталонная модель описывается уравнением:
![]() ,
(2)
,
(2)
где
 ,
,
 ,
,
 - переменные состояния.
- переменные состояния.
Закон адаптивного управления с параметрической настройкой (без огрубления) имеет вид
![]() (3)
(3)
 (4)
(4)
где
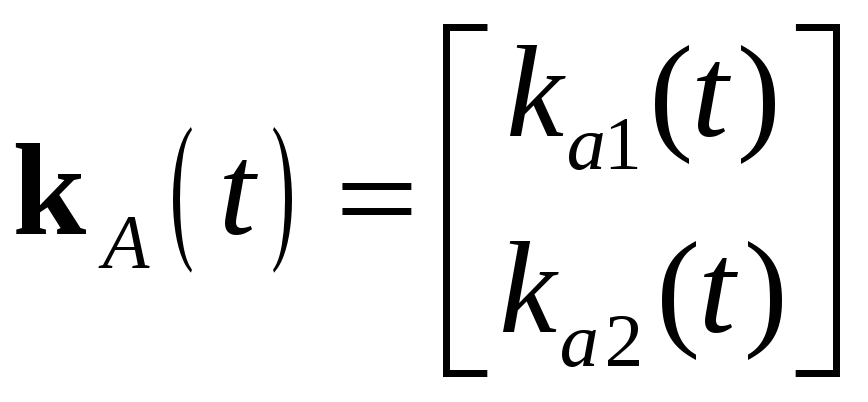 – вектор-строка настраиваемых
коэффициентов, а
– вектор-строка настраиваемых
коэффициентов, а
![]() – настраиваемый входной коэффициент
адаптивного закона;
– настраиваемый входной коэффициент
адаптивного закона;
 - диагональная, положительно определенная
матрица;
- диагональная, положительно определенная
матрица;
![]() – положительный коэффициент усилений
настроек;
– положительный коэффициент усилений
настроек;
![]() – вектор ошибок – разностей между
переменными состояния объекта (5) и
эталонной модели (6),
– вектор ошибок – разностей между
переменными состояния объекта (5) и
эталонной модели (6),
![]() матрица Р
удовлетворяет
уравнению Ляпунова имеющему единственное
решение
матрица Р
удовлетворяет
уравнению Ляпунова имеющему единственное
решение
![]() в
силу гурвицевости
в
силу гурвицевости
![]() для любой симметричной положительно
определенной
для любой симметричной положительно
определенной
![]() матрицы
матрицы
![]() .
.
Задание:
-
Построить и исследовать моделированием объект управления (1) с заданными параметрами
 для устойчивого случая.
для устойчивого случая. -
Построить эталонную модель (2) и сравнить ее динамику с динамикой объекта управления (1).
-
Построить адаптивное управление (3) с настройками (4) и начальными значениями
 по своему варианту.
по своему варианту. -
Исследовать адаптивную систему, изменяя коэффициенты
 (
( ).
).
-
Записывать установившиеся значения для
 и
и
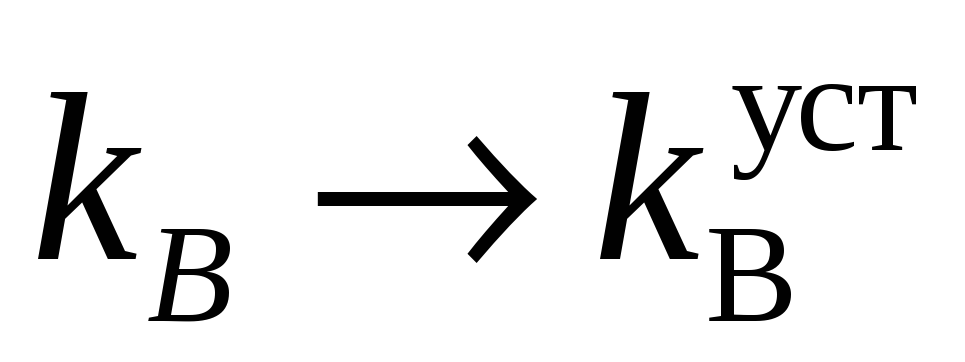 и сравнивать их со значениями, полученными
из формул
и сравнивать их со значениями, полученными
из формул
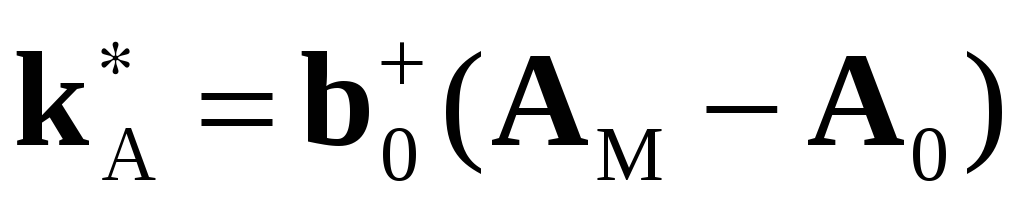 ,
,
 .
. -
Сделать выводы о работе адаптивной системы с параметрической настройкой для управления устойчивым объектом.
-
Построить и исследовать моделированием объект (1) с заданными параметрами
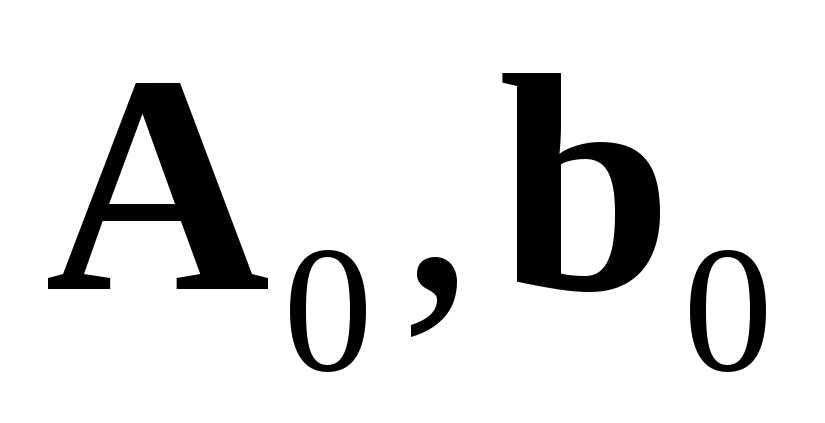 для неустойчивого случая.
для неустойчивого случая. -
Повторить п.3-6 для случая неустойчивого объекта.
Пример выполнения самостоятельной работы
Исследование объекта второго порядка
Устойчивый объект
Дано:
![]() ,
,
![]() ,
,
![]() ,
,
![]() (5)
(5)
Рассмотрим
объект второго порядка описываемый
уравнением (1), где
![]() ,
,
![]() ,
,
 - переменные состояния.
- переменные состояния.
Исследуем
моделированием систему при следующих
значениях:
![]() ,
,
![]() ,
,
![]() .
Полученный переходный процесс представлен
на рисунке 1 (
.
Полученный переходный процесс представлен
на рисунке 1 (![]() ).
).

Рисунок 1 - Переходный
процесс при
![]() ,
,
![]() ,
,
![]()
Построим адаптивное управление объектом (1), задавая желаемые переходные процессы объекта с адаптивным управлением с помощью эталонной модели (2).
Проведем
моделирование эталонной модели и сравним
траектории эталонной модели (см. рисунок
2) и самого объекта управления (см. рисунок
1) при следующих значениях
![]() ,
,
![]() ,
,
![]() (
(![]() )
)

Рисунок 2 - Переходный
процесс при
![]() ,
,
![]() ,
,
![]()
Сравнивая графики, можно сделать вывод о том, что быстродействие эталонной модели возросло в 3 раза по сравнению с объектом регулирования, а переходный процесса имеет апериодический вид.
Построим систему адаптивного управления с параметрической настройкой без огрубления.
Проведем
моделирование адаптивной системы
(1)÷(4) при числовых параметрах системы,
приведенных в (5), изменяя только значения
коэффициентов усиления настроек
![]()
1)![]() ,
,
![]() ,
,
![]()
![]() ,
,

Рисунок 3 - Переходный
процесс при

.
.
.
*)![]() ,
,
![]() ,
,
![]() ,
,
![]()

Рисунок * - Переходный
процесс при

С
увеличением значений коэффициентов
усиления
![]() влияние адаптивного регулятора
возрастает, и динамика всей системы
стремится к динамике эталонной модели.
влияние адаптивного регулятора
возрастает, и динамика всей системы
стремится к динамике эталонной модели.
Моделирование системы с неустойчивым объектом
Дано:
 ,
,
 ,
,
![]() ,
,
 (6)
(6)
Построим
и промоделируем объект с
 и получим переходный процесс вида (см.
рисунок ) :
и получим переходный процесс вида (см.
рисунок ) :
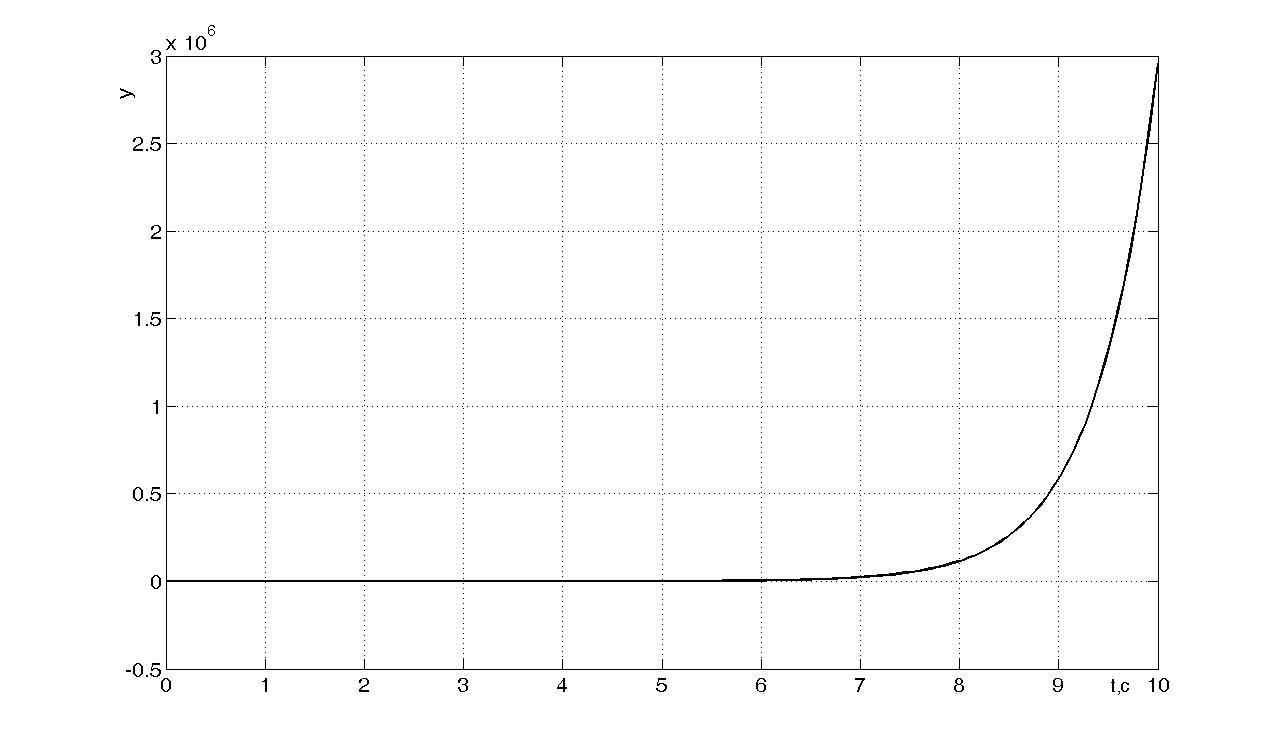
Рисунок - Переходный
процесс при
![]()
Как
в случае устойчивого объекта, будем
менять только
![]() и проведем моделирование адаптивной
системы при следующих параметрах
системы:
и проведем моделирование адаптивной
системы при следующих параметрах
системы:
1)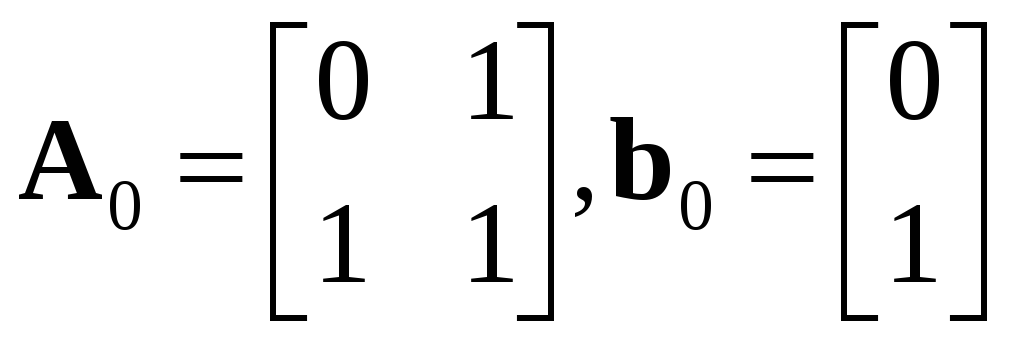 ,
,
![]() ,
,
 ,
,

Рисунок - Переходный
процесс при
![]()
.
.
.
m) ,
,
![]() ,
,
 ,
,
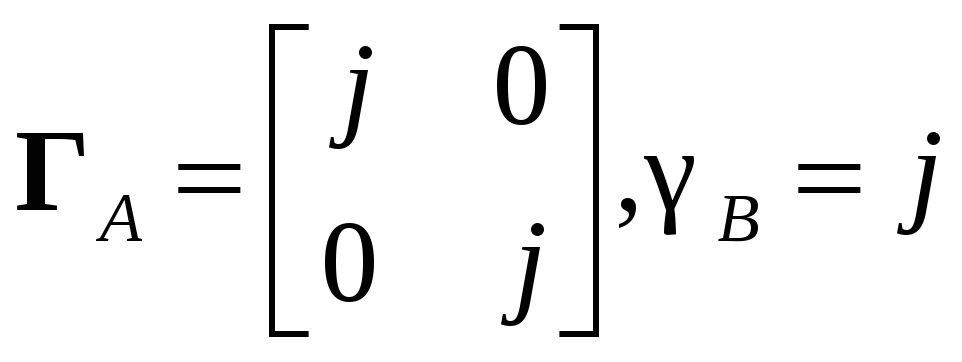

Рисунок - Переходный
процесс при
![]()
Для
системы с параметрами (6) значения
настроек
![]() и
и
![]() по графикам переходных процессов будут:
по графикам переходных процессов будут:
![]() ,
,
![]() ,
,
![]() .
Значения
.
Значения
![]() и
и
![]() рассчитываются по формулам:
рассчитываются по формулам:
![]() ,
,
![]() ,
(7)
,
(7)
где
![]() - псевдообращение вектора
- псевдообращение вектора
![]() .
.
Анализ
процессов, как и в случае с объектом
первого порядка, показывает, что
адаптивный регулятор справляется с
задачей стабилизации объекта управления
и, как было описано выше, чем выше значения
коэффициентов усиления
![]() ,
тем сильнее влияние адаптивного
регулятора на объект, выше частота
колебаний переходного процесса и меньше
перерегулирование. При достаточно
больших коэффициентах усиления
,
тем сильнее влияние адаптивного
регулятора на объект, выше частота
колебаний переходного процесса и меньше
перерегулирование. При достаточно
больших коэффициентах усиления
![]() переходный процесс системы с адаптивным
регулятором совпадает с переходным
процессом в эталонной модели.
переходный процесс системы с адаптивным
регулятором совпадает с переходным
процессом в эталонной модели.
Варианты заданий.
Вариант №1
Второй порядок
Устойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Неустойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Вариант №2
Второй порядок
Устойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Неустойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Вариант №3
Второй порядок
Устойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Неустойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Вариант №4
Второй порядок
Устойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Неустойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Вариант №5
Второй порядок
Устойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
Неустойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
Вариант №6
Второй порядок
Устойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
Неустойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
Вариант №7
Второй порядок
Устойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
Неустойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Вариант №8
Второй порядок
Устойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Неустойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Вариант №9
Второй порядок
Устойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Неустойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Вариант №10
Второй порядок
Устойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Неустойчивый объект
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
