51. Критические точки.

Критические точки – точки, подозрительные на экстремум.

Если производная функции в точкеравна нулю или не существует, то эта точка – подозрительная на экстремум (критическая точка).

Каждая точка экстремума – критическая (но не наоборот).

52. Достаточные условия экстремума.

Достаточное условие экстремума. Если непрерывная функция , дифференцируема в некоторой окрестности точкии при переходе через нее производная меняет свой знак, то- точка экстремума.

Если при переходе через точку экстремума производная меняет свой знак с плюса на минус, то эта точка – точка максимума, если с минуса на плюс – точка минимума.

53. Исследование функций с помощью производных высших порядков.

Если функция во всех точках (a;b) имеет положительную (отрицательную) вторую производную, то график функции на этом интервале выпуклый вниз (вверх).

54. Выпуклость и вогнутость кривой.

График дифференцируемой функции называетсявыпуклым вниз на интервале (a;b), если он расположен выше любой касательной на этом интервале, выпуклым вверх, если он расположен ниже.

55. Точки перегиба.

Точка, при переходе через которую график функции переходит с одной стороны касательной на другую (вторая производная меняет свой знак) называется точкой перегиба.

56. Асимптоты.

Асимптота кривой – прямая, расстояние от которой до точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат от этой точки по кривой.

Асимптоты могут быть вертикальными, наклонными и горизонтальными

Прямая являетсявертикальной асимптотой графика функции , если, или, или

Уравнение наклонной асимптоты будем искать в виде y = kx + b. ,.

Горизонтальная асимптота – частный случай наклонной (когда ),

57. Схема исследования функций.

1. Область определения функции (D(y))

2. Точки пересечения графика с осями координат

3. Интервалы знакопостоянства

4. Четность\нечетность (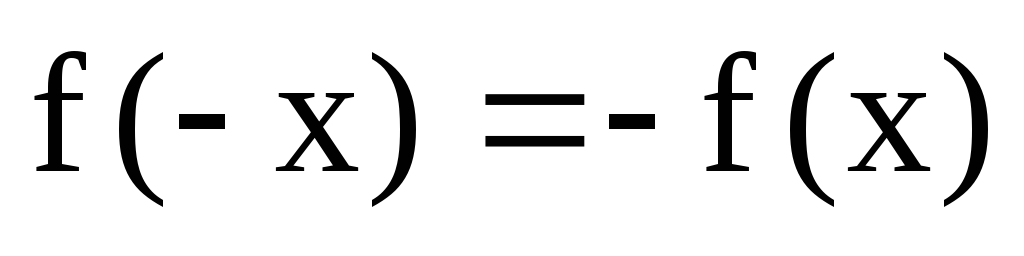- нечетная,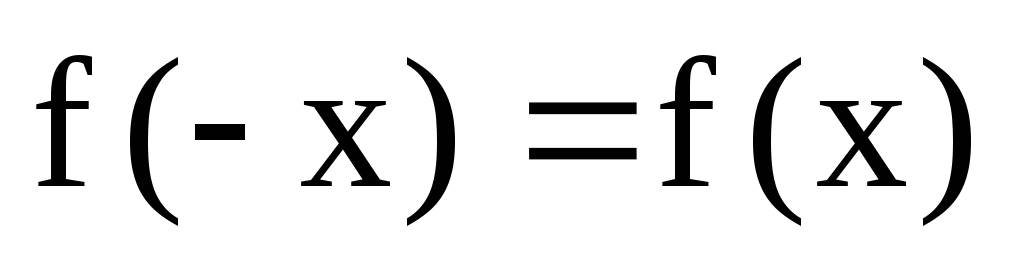- четная)

5. Асимптоты

6. Интервалы монотонности (возрастание\убывание)

7. Экстремумы (минимумы\макимумы)

8. Интервалы выпуклости\вогнутости и точки перегиба

58. Неопределенный интеграл.

Функция F(x) называется первообразной функции f(x) на интервале (a;b), если для любого выполняется равенство(или)

Если функция F(x) является первообразной функции f(x) на (a;b), то множество всех первообразных для f(x) задается формулой F(x) + C, где C – постоянное число.

Множество всех первообразных функций F(x)+C для f(x) называется неопределенным интегралом от функции f(x) и обозначается символом

, f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение, х – переменная интегрирования, - знак неопределенного интеграла.

59. Свойства неопределенного интеграла.

1) Дифференциал от неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции .

2) Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной

3) Постоянный множитель можно вынести за знак интеграла

4) Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых.

5) (Инвариантность формулы интегрирования). Если , то и, где- произвольная функция, имеющая постоянную производную