1
ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №11. Тэттэр А.Ю., Ковалева Т.В., Пономарев
2
Связь между уравнениями электрических и магнитных цепей
и уравнениями электромагнитного поля (ЭМП)
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №11. Тэттэр А.Ю., Ковалева Т.В., Пономарев
ЭМП – форма существования материи. |
3 |
|
Поле и вещество взаимопреобразуемы:
E mc2 ,
где E – энергия, m – масса,
c – скорость света.
ЭМП обладает массой, что подтверждено открытым Лебедевым световым давлением.
Энергия переносится излученным ЭМП.
ЭМП состоит из физически неразделимых
электрической и магнитной составляющих.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №11. Тэттэр А.Ю., Ковалева Т.В., Пономарев
В случае стационарных (неизменных во времени) |
4 |
|
|
полей их можно рассматривать независимо друг от |
|
друга. |
|
Стационарные электрические поля создаются |
|
неподвижными зарядами или постоянными токами. |
|
Магнитное поле создают движущиеся заряды. |
|
Стационарное магнитное поле создается |
|
постоянным током. |
|
Среды, в которых существуют электромагнитные поля подразделяются на однородные и неоднородные.
Среди неоднородных сред часто рассматривают слоистые среды (воздух – земля).
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №11. Тэттэр А.Ю., Ковалева Т.В., Пономарев
5
В линейных средах параметры
–диэлектрическая проницаемость ε (Ф/м);
–магнитная проницаемость μ (Гн/м);
–удельная проводимость γ (См/м)
не зависят от характеристик поля:
–напряженности E (В/м);
–магнитной индукции В (Тл);
–плотности тока J (А/м2).
В нелинейных – зависят.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №11. Тэттэр А.Ю., Ковалева Т.В., Пономарев
В изотропных средах ε, μ, γ одинаковы во всех |
6 |
|
|
направлениях. |
|
В анизотропных средах по разным направлениям они могут отличаться.
Электрические токи существуют не только
в проводниках, но и в диэлектриках, безвоздушной среде, а также в земле
(блуждающие токи, которые разрушают металлические конструкции).
На проводящие свойства воздуха влияет влажность и запыленность.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №11. Тэттэр А.Ю., Ковалева Т.В., Пономарев
7
Рассчитать количественные характеристики подобных явлений используя законы электрических цепей не всегда возможно.
На помощь приходят уравнения ЭМП, устанавливающие связь между векторами
E, J , H , B во всех точках пространства.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №11. Тэттэр А.Ю., Ковалева Т.В., Пономарев
8
Первый закон Кирхгофа
для электрической цепи
I1 |
I2 |
I 0; |
I1 I2 I3 0; |
|
|
I3 |
|
||
|
|
|
|
|
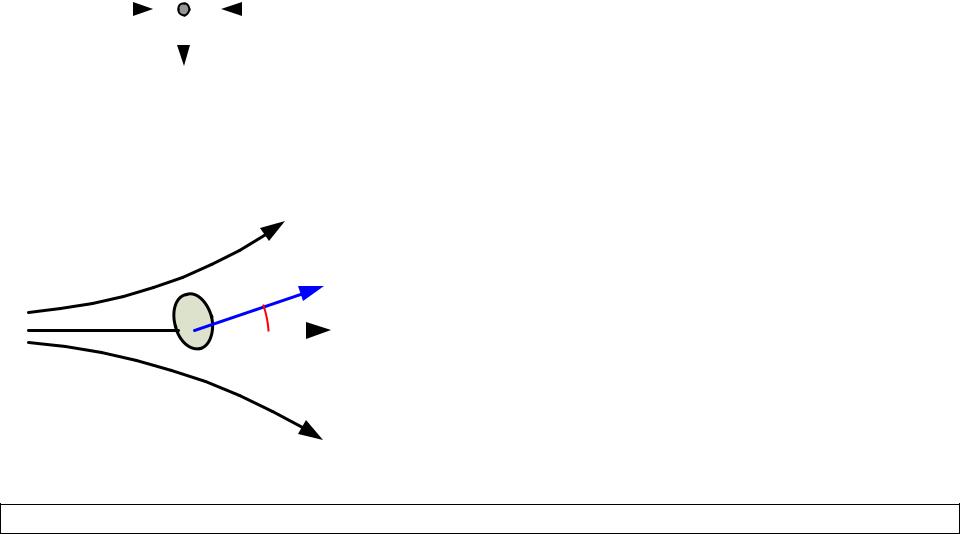
Электрическое поле
|
|
|
|
Ток через площадку S: |
||||||
|
|
dS |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
J |
I |
|
|
|
|
||||
S |
|
|
|
JdS JS cos . |
||||||
|
|
|
|
|
|
S |
||||
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №11. Тэттэр А.Ю., Ковалева Т.В., Пономарев
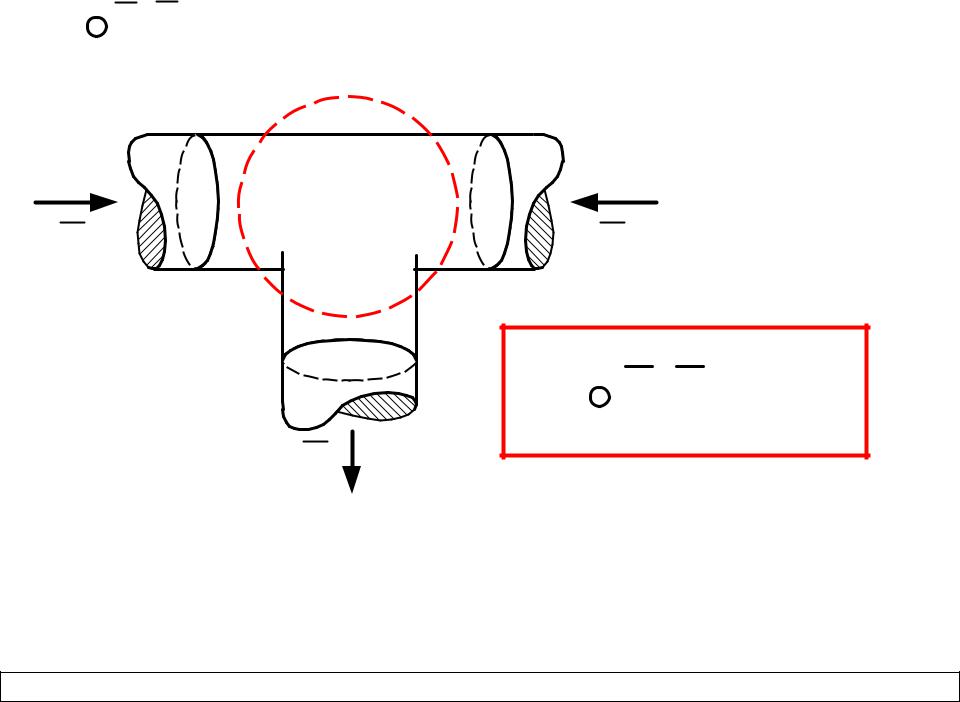
JdS J1S1 J2S2 J3S3 I1 I2 I3 0. |
9 |
||||
|
|||||
S |
S1 |
S |
|
S2 |
|
|
|
|
|
||
I1 |
|
|
|
I2 |
|
J1 |
|
|
|
J2 |
|
|
|
|
S3 |
JdS 0. |
|
|
J3 |
I3 |
|
|
|
|
|
|
|
||
Принцип непрерывности электрического тока в интегральной форме
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №11. Тэттэр А.Ю., Ковалева Т.В., Пономарев
10
В теории ЭМП используются также
соотношения в дифференциальной форме,
которые получаются путем предельного перехода к бесконечно малому контуру или поверхности интегрирования.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №11. Тэттэр А.Ю., Ковалева Т.В., Пономарев
|
|
|
|
|
|
|
|
|
|
|
11 |
||
lim |
JdS |
div |
|
; |
|
div |
|
0. |
|
|
|||
J |
J |
||||||||||||
V 0 |
V |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
Принцип непрерывности электрического тока в дифференциальной форме
J |
A J |
div – дивергенция (исток) |
|
|
div J 0 означает, что линии плотности тока не имеют начала и конца, токи протекают по замкнутым путям.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №11. Тэттэр А.Ю., Ковалева Т.В., Пономарев
12
Первый закон Кирхгофа
для магнитной цепи
Ф1 |
Ф2 |
|
|
Ф3 |
|
0; 1 2 3 0; |
|
|
|
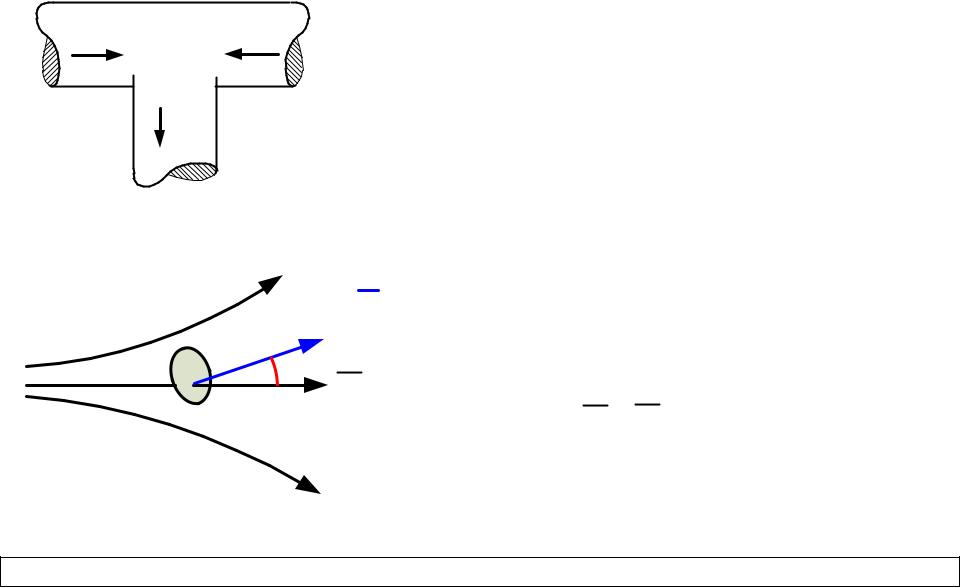
Магнитное поле |
|
|
|
dS |
Магнитный поток через |
|
|
площадку S: |
|
|
B |
||
|
|
||
|
S |
|
BdS BS cos . |
|
|
|
|
S
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №11. Тэттэр А.Ю., Ковалева Т.В., Пономарев
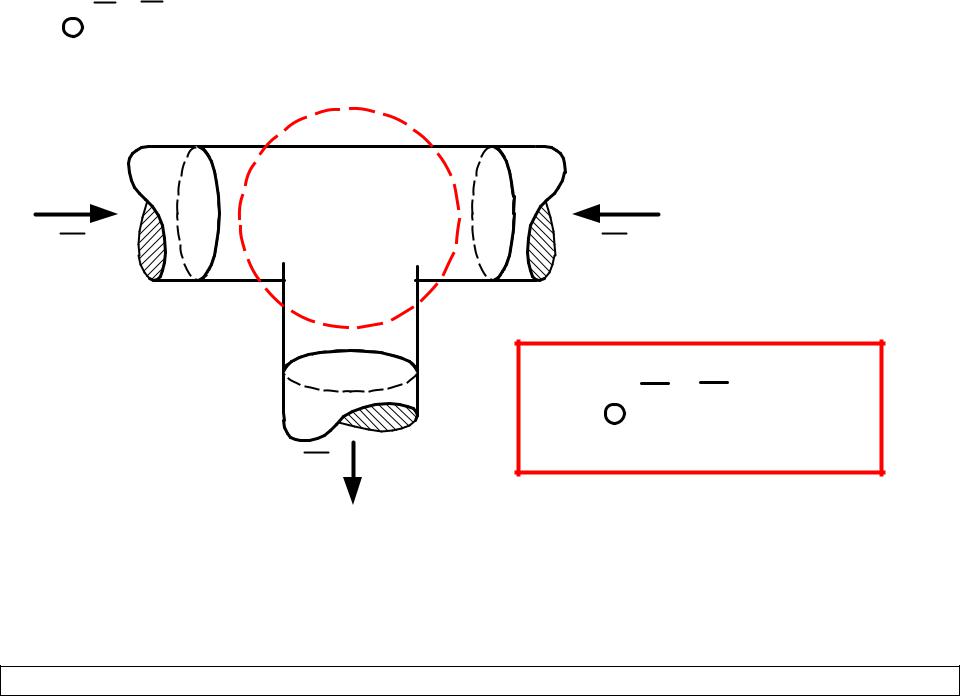
BdS B1S1 B2S2 |
B3S3 1 2 3 0. 13 |
||
S |
S |
|
|
S1 |
S2 |
||
|
|||
Ф |
1 |
Ф2 |
|
|
|
||
B1 |
|
B2 |
|
|
S3 |
BdS 0. |
|
B3 |
Ф3 |
||
|
Принцип непрерывности магнитного потока в интегральной форме
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №11. Тэттэр А.Ю., Ковалева Т.В., Пономарев
14
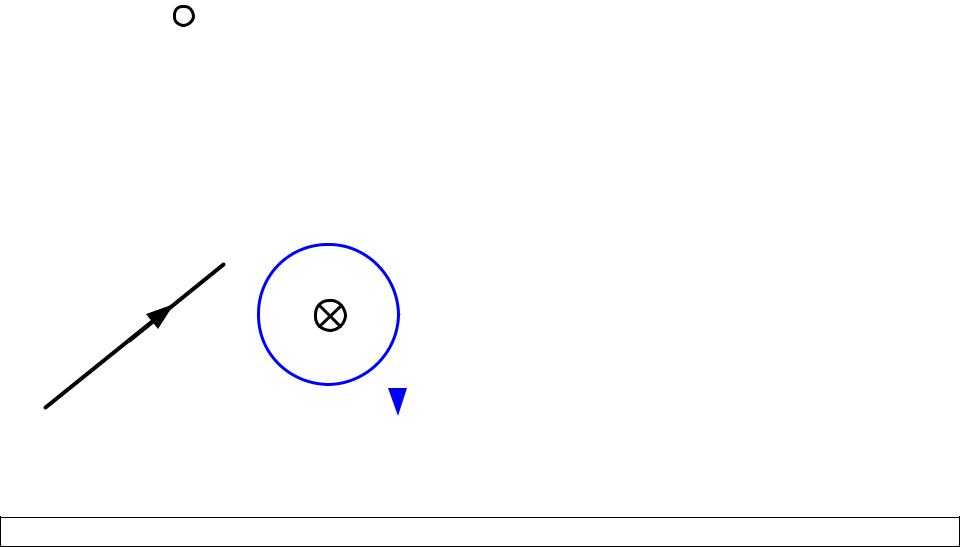
Переход к дифференциальной форме
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
BdS |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
div |
|
0. |
|
||||
lim |
S |
|
div |
|
; |
|
B |
|
|||||
|
B |
||||||||||||
V |
|
||||||||||||
V 0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
I |
I |
|
|
Линии вектора магнитной |
|
|
индукции В замкнуты, |
||||
|
|
|
|
|
|
|
B |
||||
|
|
|
|
|
не имеют начала и конца. |
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №11. Тэттэр А.Ю., Ковалева Т.В., Пономарев
15
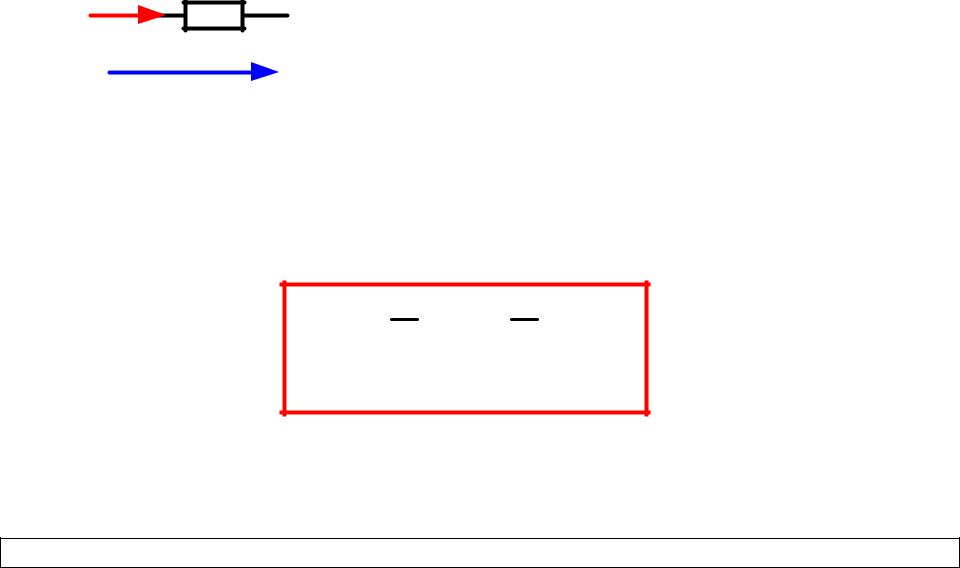
Закон Ома
I r
U
|
|
I |
|
|
|
|
U |
|
J |
||||
gU; |
g |
|||||
I r |
||||||
U |
|
|
||||
|
|
E |
||||
Закон Ома в дифференциальной форме:
J E.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №11. Тэттэр А.Ю., Ковалева Т.В., Пономарев
|
|
|
|
Закон Ома для участка цепи с ЭДС |
16 |
|||||||||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
(второй закон Кирхгофа) |
|
||||||||||||||
a I |
r |
|
E |
|
|
|
b |
|
|
U |
ab |
E |
g Uab E ; |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Uab |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
стор , |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
J |
E |
E |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где Eстор – напряженность стороннего поля (неэлектростатического происхождения).
Например, в гальванических элементах поле имеет электрохимическую природу.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №11. Тэттэр А.Ю., Ковалева Т.В., Пономарев