Расчет контактных напряжений в системе
«колесо – рельс»
По теории Герца давления между двумя соприкасающимися цилиндрами с параллельными осями распределяются на площади контакта по закону поверхности эллипсоида; площадка контакта — эллипс.
Эллиптический закон распределения давлений получен при следующих допущениях:
-материалы соприкасающихся деталей следуют закону Гука;
-контактирующие поверхности однородны и изотропны;
-сжимающая сила направлена по нормали к площади контакта;
-силы трения в зоне контакта не действуют;
-размер контактной площадки мал по сравнению с размерами контактирующих тел;
Если в области контакта имеются более двух радиусов кривизны, следует использовать негерцевское решение. Это относится к изношенным профилям колеса и рельса.
Главные радиусы кривизны поверхностей тел в точке касания обозначены:
11 |
– радиус поверхности |
катания гибкого бандажа; |
|
12 |
- радиус поверхности |
катания колеса (прокат стандартного колеса);
11 – радиус поперечного профиля поверхности катания рельса ( 12
- для неизношенной поверхности катания рельса, |
0,015м - для |
|
изношенной поверхности катания рельса); |
12 |
|
|
|
|
22 – радиус продольной поверхности катания рельса вызванного прогибом и геометрической неровностью ( 12 - для абсолютно ровной поверхности катания и жесткого верхнего строения пути);
При |
11 12 |
|
21 22 |
|
|
|
|
|
|
||||||
этом |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
1 |
||
Главные кривизны: |
k |
|
|
1 |
k |
|
|
k21 |
|
k22 |
|
||||
|
|
|
|||||||||||||
|
|
21 |
22 |
||||||||||||
|
; |
||||||||||||||
12 |
|||||||||||||||
|
12 |
|
11 |
|
|
|
|
|
|||||||
Принято, что площадка контакта представляет собой эллипс, полуоси которого α (большая ось) и b (малая ось) определяются следующими выражениями:
|
3PЭ(1 2) |
b |
a |
. |
|||
|
|
||||||
a 3 |
|
|
|
|
|
||
E(k11 |
k12 |
k21 k22) |
|||||
|
|
|
|
||||
где РЭ - эквивалентная сила, направленная по нормали к площадке |
||||
точки контакта, равная |
|
|
; |
|
Р |
Р2 |
Р2 |
||
|
||||
|
Э |
Z |
Y |
|
Значения коэффициентов α и β приведены в табл. 8.2 [Бирюков] Наибольшее давление в центре площадки
q 3PЭ 0 2 ab
Давление в произвольной точке М(х, у) площадки контакта
p q0 1 ax 2 by 2
Распределение нормальных герцевских напряжений на
площадке контакта Форма площадки контакта и распределение давлений: ρ11 = 355,6
мм; ρ22 = 291,6 мм;
ρ12 = ρ21 =∞; P = 100 кН; p Tm = 1170 МПа.
Тангенциальная задача
•Движение стандартной колесной пары сопровождается постоянным проскальзыванием в точке контакта колесо - рельс в продольном и поперечном направлениях.
•Контактные касательные напряжения, обусловленные тяговым моментом, определяются по следующему уравнению
• |
|
|
|
PZ |
|
где |
– площадь контактного эллипса ( |
||||
• |
|
|
|
|
|
|
|
|
|||
μ – коэффициент трения вX зонеFконтакта; |
|||||
• |
|
|
|
K.Э |
|
– Вертикальная нагрузка на колесо. |
|||||
FK.Э
);
FK.Э ab
PZ
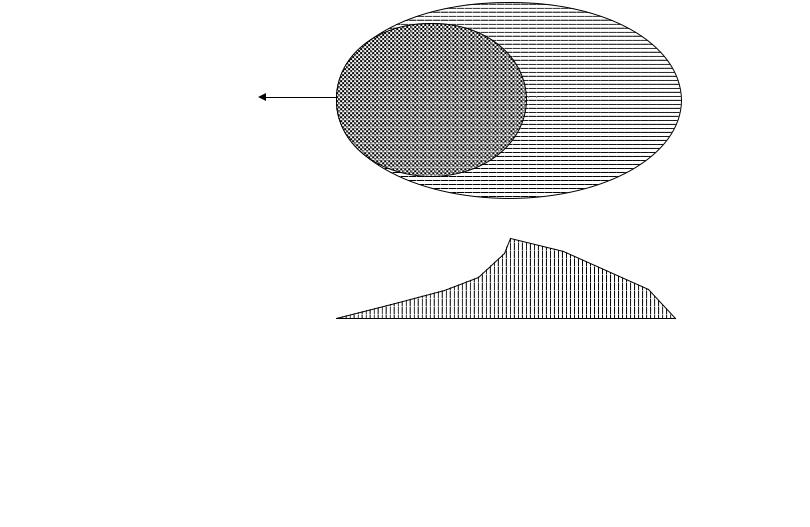
При тангенциальных (тяговых) усилиях в направлении качения на передней части площадки контакта имеет место зона сцепления, а на задней — зона микроскольжения.
Направление
движения
Сцепление Микроскольжение
Распределение касательных усилий по площадке контакта
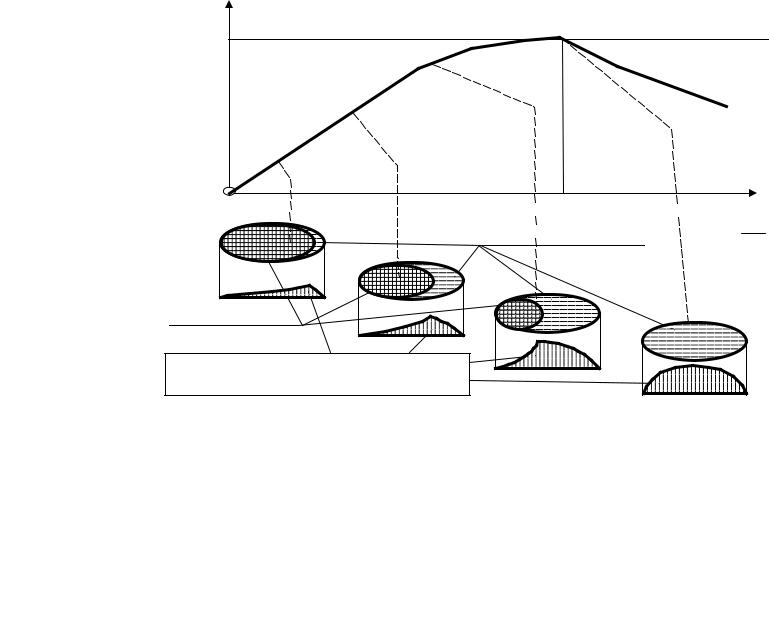
Распределение продольных сил тяги (сил крипа) по площадке контакта
fN |
0,2-10% 
Микроскольжение
u V
Сцепление
Распределение касательных усилий на площадке контакта
Расчеты показывают, что непосредственно под площадкой контакта материал находится в трехосном напряженном состоянии. Три компоненты тензора напряжения примерно равны, в результате чего достигается высокий уровень несущей способности материала. Далее вглубь материала эти напряжения становятся неравными, и уровень максимальных касательных напряжений достигает своего наивысшего значения.
2,0
1,5
Глубина от поверхнос
ти, мм
1,0
0,5
0 0,2 0,4 0,6 0,8 1,0
Относительное напряжение
Напряжения под контактной площадкой при действии нагрузки:
Z /q0 |
- нормальные напряжения; |
Y /q0 |
и Х /q0 - напряжения параллельные площадке контакта |
1/q0 - максимальное касательное напряжение.
Микротрещины , и дефекты на поверхности катания бандажа
Извилистое движение одиночной колесной пары
•Двигаясь по прямым участкам пути, экипаж описывает сложную волнообразную траекторию. Такое сложное движение называется извилистым, в процессе которого в экипажах возникают большие силы инерции, создающие значительное
боковое давление колес на рельсы, что и является одной из основных причин ограничения скорости движения поезда.
•Изучение извилистого движения начинают с рассмотрения движения одиночной колесной пары. Выбирают два крайних случая: первый, простой — движение одиночной колесной пары без проскальзывания колес по головкам рельсов; второй, более сложный — движение с непрерывным скольжением. В действительности, вероятно, одиночная колесная пара движется попеременно то без скольжения, то со скольжением.