zaLrOavrsu

4.3.Содержание отчета

1.Цель работы, схемы измерений.

2.Заполненные табл. 4.1 и 4.2.

3.Пример расчета Iстаб.

4.Графики ВАХ стабилитрона и варистора.

5.Выводы (с анализом полученных характеристик).

Лабораторная работа № 5 ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИК КОНДЕНСАТОРОВ

ПОСТОЯННОЙ ЕМКОСТИ

Цель работы – ознакомление с различными видами конденсаторов по-

стоянной емкости, в том числе электролитическими; исследование темпера-

турной стабильности емкости и тока утечки конденсаторов.

5.1. Основные сведения о конденсаторах

Конденсатор, как следует из его названия, предназначен для «конденси-

рования» (накопления) электрического заряда. Любые два проводника, раз-

деленные диэлектриком, образуют конденсатор. Заряд конденсатора (Q) и

накопленная в нем энергия (W) связаны с напряжением (U) на его электродах и его емкостью (С) выражениями Q = CU и W = CU 22.

При расчетах в СИ емкость конденсатора выражают в фарадах [Ф]. Ре-

альные конденсаторы обычно имеют емкость, составляющую миллиардные,

миллионные или тысячные доли фарада. Поэтому для маркировки их емкости используются производные единицы: пикофарады (1 пФ = 10–12 Ф), нанофарады (1 нФ = 1000 пФ = 10–9 Ф) и микрофарады (1 мкФ = 1000 нФ = 10–6 Ф).

Наиболее часто емкость указывают на корпусе конденсатора в явном виде, например: 510 пФ; 15 нФ; 0,022 мкФ; 100 мкФ. На зарубежных конден-

саторах те же номинальные значения имеют следующую маркировку: 510 pF; 15 nF; 0,022 µF; 100 µF. На микроминиатюрных конденсаторах принято не указывать единицы измерения: их емкость всегда выражают в пикофарадах числовым кодом, в котором первые две цифры являются значащими, а по-

следняя цифра указывает степень N множителя 10N. Например, маркировка

«102» на корпусе конденсатора означает емкость 10 · 102 пФ = 1000 пФ, а «223» означает 22 · 103 пФ = 22 000 пФ = 22 нФ или 0,022 мкФ.

21

Допустимые отклонения емкости конденсатора от номинального значе-

ния обычно связаны с температурными нестабильностями в диапазоне рабо-

чих температур. На пленочных, бумажных и электролитических конденсато-

рах допуск приводится в маркировке и указывается в процентах, например: ±5 %; ±10 %; ±20 %. Здесь принято два вида обозначений допуска. Для кон-

денсаторов с предсказуемой монотонно изменяющейся зависимостью емко-

сти от температуры, т. е. с известным значением температурного коэффици-

ента емкости (ТКЕ), введены группы термостабильности, указываемые на корпусе конденсатора вместе с его номинальной емкостью (табл. 5.1).

Для этой группы конденсаторов во всем диапазоне рабочих температур с определенным допуском, достигающим ±20–100 % от объявленной величи-

ны, ТКЕ может быть задан как постоянная величина, рассчитываемая по формуле

Обозначение группы термостабильности конденсаторов отечественного производства, у которых в пределах рабочих температур изменение емкости не имеет монотонного характера, начинается с русской буквы Н, далее ука-

зывается двухзначное число, обозначающее допуск (в процентах) изменения

емкости (табл. 5.2).

22

Температура оказывает влияние не только на значение емкости конденсатора, но и на его ток утечки, характеризующий электрическую прочность изоляции. Температурное изменение тока утечки особенно велико у электролитических конденсаторов. Для электролитических конденсаторов с алюминиевыми электродами максимальный ток утечки [мкА] в рабочем диапазоне температур (обычно от –40 до +85 ° С) вычисляется по следующей эмпирической формуле:

Iут ≤ 0,01СU (для СU ≤ 1000) или Iут ≤ 0,03СU (для СU > 1000), (5.2)

где С – емкость, мкФ; U – напряжение, В.

Зависимости тока и напряжения на конденсаторе во время переходных процессов в RC-цепях с источниками постоянного напряжения описываются

где U∞ – напряжение на конденсаторе после окончания переходного процес-

са, т. е. для времени t = ∞; U0 – напряжение на конденсаторе в момент начала переходного процесса, т. е. для t = 0; τ = RC – постоянная времени цепи зарядки/разрядки.

Если конденсатор изначально не заряжен (U0 = 0), а к моменту полной зарядки (при t = ∞) напряжение на нем становится равным напряжению ис-

точника питания (U∞ = Uп ), то формула (5.3) приобретает вид

5.2.Порядок выполнения исследований

1.Исследовать температурную зависимость емкости многослойного конденсатора с однонаправленными выводами и керамикой типа Y5V и многослойного планарного конденсатора с керамикой Х7R, для чего собрать схему,

23

Рис. 5.1. Схема проведения измерений ТКЕ керамических конденсаторов

изображенную на рис. 5.1, и провести измерения, повышая температуру обогревателя до 90 ° С. По результатам измерений заполняется табл. 5.3. Результаты измерений занести в протокол (первые три строки табл. 5.3).

Значения αС рассчитываются с помощью (5.1).

2. Для исследования тока утечки алюминиевого электролитического конденсатора с номинальной емкостью 100 мкФ измерить с помощью мультиметра 1 сопротивление балластного резистора ( Rб), результаты измерений занести в протокол.

Рис. 5.2. Схема измерений температурной зависимости тока утечки алюминиевого электролитического конденсатора

24

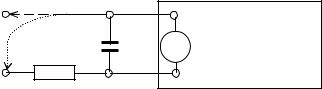
3. Собрать схему, представленную на рис. 5.2. При подключении кон-

денсатора С к зажимам «Cx, Rx» следует помнить, что электролитический конденсатор является полярным, и важно, чтобы положительный полюс кон-

денсатора (+) подключался к положительному полюсу источника.

4. После сборки схемы зарядить исследуемый конденсатор до напряже-

ния источника питания, замкнув накоротко балластный резистор при помощи

перемычки на 5…10 с.

5. Ток утечки определяется с помощью мультиметра 1 по падению напря-

жения на Rб. Такой способ измерения тока вызван отсутствием в применяемых мультиметрах пределов измерения токов, рассчитанных на единицы микроам-

пер. Результаты измерений зависимости падения напряжения на балластном ре-

зисторе от температуры занести в протокол (первые две строки табл. 5.4).

6. Для исследования процессов зарядки и разрядки электролитического конденсатора с номинальной емкостью 1000 мкФ измерить с помощью муль-

тиметра 1 сопротивление Rб, результаты измерений занести в протокол.

7. Собрать схему, представленную на рис. 5.3, и разрядить конденсатор,

замкнув его выводы накоротко на несколько секунд.

8. Приготовить секундомер, включить стенд и через каждые 15 с за-

писывать в протокол показания вольтметра до тех пор, пока напряжение

(Uз. э) заряжаемого конденсатора не станет равным 15 В. Для исследова-

ния процесса разрядки конденсатора отключить положительный полюс конденсатора от источника напряжения и замкнуть его на общую точку

(пунктирная линия на рис. 5.3).

Рис. 5.3. Схема исследования процессов зарядки и разрядки конденсатора

25

Через каждые 15 с записывать в протокол показания вольтметра до тех пор, пока напряжение конденсатора (Uр. э) не станет равным 1 В (первые три строки табл. 5.5).

5.3.Содержание отчета

1.Цель работы, схемы измерений.

2.Заполненные табл. 5.3–5.5.

3.Примеры расчета ТКЕ αС конденсатора и тока утечки.

4.Графики зависимостей емкости и ТКЕ от температуры.

5.Графики экспериментальной и теоретической (по (5.2)) зависимостей тока утечки от температуры.

6.Графики экспериментальной и теоретической (по (5.4) и (5.5)) зависимо-

стей изменения напряжения на конденсаторе при его зарядке и разрядке (для удобства анализа рекомендуется все 4 графика выполнять на одном рисунке).

7. Выводы (с анализом полученных характеристик).

Лабораторная работа № 6 ИССЛЕДОВАНИЕ ПАРАМЕТРОВ КАТУШЕК ИНДУКТИВНОСТИ

Цель работы – ознакомление с основными параметрами катушек ин-

дуктивности и методами их измерений.

6.1. Основные сведения об индуктивностях

Движущиеся заряды (токи) порождают магнитное поле. Магнитное поле имеет направленный характер и характеризуется векторной величиной В,

называемой электромагнитной индукцией. Было бы логично присвоить вели-

чине В, по аналогии с напряженностью электрического поля Е, название напряженность магнитного поля. Однако по историческим причинам это название носит вспомогательная величина Н, аналогичная вектору электри-

ческого смещения D. Связь между В и Н определяется следующей формулой:

26

В = µ0µН,

где µ0 = 4π×10–7 Гн/м – магнитная проницаемость вакуума (воздуха); µ – от-

носительная магнитная проницаемость вещества по отношению к вакууму. Магнитное поле удается сконцентрировать внутри катушки, образован-

ной множеством близко расположенных витков с током I. Если принять, что все составляющие индукции по сечению катушки S равны некоторому среднему значению В, что справедливо для катушек с сердечником, то отдельные значения В суммируются в полный поток электромагнитной индукции, или

где L – коэффициент пропорциональности между током и полным магнитным потоком катушки, называемый индуктивностью катушки. Индуктивность зависит от геометрии катушки, от магнитной проницаемости сердечника и от магнитных свойств окружающей среды. Так, для дросселей с замкнутыми тороидальными магнитопроводами индуктивность определяется формулой

где N – количество витков; S – сечение магнитопровода; lср – средняя длина

окружности, определяемая как полусумма длин окружностей внутреннего и внешнего контуров магнитопровода. В лабораторной работе используется сердечник с µ = 2000, lср = 26 мм, S = 108 мм2.

Единицей индуктивности является генри [Гн]. Одному генри соответствует индуктивность катушки без сердечника, которая развивает поток электромагнитной индукции в 1 Вб (вебер) в результате протекания тока 1 А.

В соответствии с законом Ленца изменение магнитного потока Ф, пронизывающего замкнутый контур, порождает в нем возникновение индуцированной ЭДС (Е):

С учетом (6.1) из (6.2) получаем выражение для ЭДС катушки индуктивности при изменении протекающего через нее тока:

Е = -L dI . dt

27

Из (6.3) следует, что включение индуктивности последовательно с цепью нагрузки, питаемой от пульсирующего источника тока, снижает его пульсации за счет возникающей ЭДС самоиндукции.

Если предположить, что ток в катушке изменяется от некоторого значения I до нуля, то работа, совершаемая этим током за время dt, будет опреде-

ляться как dA = EI × dt = – LI × dI.

Если индуктивность не зависит от тока и в других элементах цепи никаких изменений не происходит, остается заключить, что магнитное поле является носителем энергии, за счет которой и совершается данная работа. Таким образом, катушка с индуктивностью L, через которую протекает ток I, запа-

сает энергию WL , равную

Катушка не может запасти энергию мгновенно. Ее нужно зарядить аналогично тому, как заряжают конденсатор. Если индуктивность подключается к источнику постоянного напряжения (U), то ее зарядка происходит по экспоненциальному закону:

I (t) = U e− τt ,

R

где R – полное активное сопротивление, ограничивающее ток индуктивности; τ = L/R – постоянная времени зарядки индуктивности.

Цепь, состоящую из катушки индуктивности и параллельно подключенного ей конденсатора, называют колебательным контуром. При работе индуктивности в составе колебательного контура, ее периодическая зарядка и разрядка происходят на резонансной частоте контура:

где С – емкость конденсатора, входящего в колебательный контур.

В колебательном контуре происходит периодическое превращение энергии,

Шунтирование конденсаторами позволяет снизить выброс напряжения на индуктивностях схемы. Используя (6.4), можно рассчитать энергию, запасае-

28

мую в катушке индуктивности при известном значении тока, а с помощью ра-

венства (6.6), найти необходимую емкость конденсатора. Основными парамет-

рами катушек индуктивности (дросселей) являются индуктивность L и внут-

реннее сопротивление R. К числу дополнительных параметров относят диапа-

зон рабочих частот, собственную резонансную частоту, температурный коэф-

фициент индуктивности (ТКИ) и добротность (Q = ωL/R). Активное сопротив-

ление катушек индуктивности легко измеряется с помощью омметра. Реактив-

ное сопротивление катушек, обладающих значительной индуктивностью, мо-

жет быть измерено на промышленной частоте f = 50 Гц. Для этого катушку подключают к источнику переменного напряжения и с помощью амперметра измеряют эффективное (действующее) значение тока. Полученный ток обу-

словлен совместным влиянием активного и реактивного сопротивлений цепи:

R2 + (ωL)2

где ω = 2πf – угловая частота.

Если индуктивность катушки невелика, то используется резонансный метод, в котором параллельно индуктивности устанавливают конденсатор с известной емкостью и измеряют частоту резонанса образованного колеба-

тельного контура. Далее по (6.5) вычисляют индуктивность L.

6.2.Порядок выполнения исследований

1.Для исследования свойств дросселя L1 с сердечником измерить его сопротивление с помощью мультиметра, результат занести в протокол.

2.Используя в качестве амперметра и вольтметра переменного тока мультиметры 1 и 2 соответственно, собрать схему, изображенную на рис. 6.1.

U1

COM

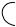Uac2

Рис. 6.1. Схема измерения индуктивности низкочастотного дросселя

29

3.Включить питание стенда и измерить переменный ток и переменное напряжение на дросселе при подаче напряжения с выходов СОМ и Uac1 и с выходов Uac1 и Uac2, результаты измерений занести в протокол.

4.Для исследования высокочастотного колебательного контура (катушки переменной индуктивности с тороидальным ферритовым сердечником, соединенной параллельно с конденсатором C = 0,047 мкФ) измерить его сопротивление с помощью мультиметра, результат занести в протокол.

5.Собрать схему, изображенную на рис. 6.2.

Рис. 6.2. Принципиальная схема (a) и монтажная схема (б) исследований высокочастотного дросселя

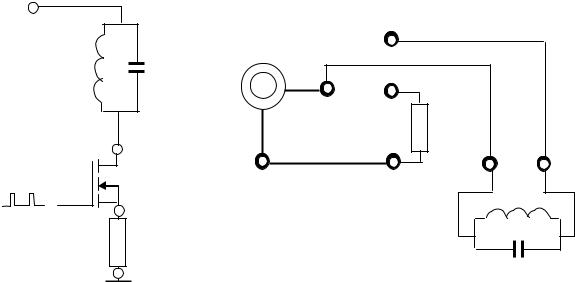
Короткие импульсы длительностью 20…30 мкс поступают на затвор ключа на полевом n-канальном транзисторе VT. В моменты воздействия импульсов транзистор отпирается (ключ замыкается) и происходит зарядка индуктивности L от регулируемого источника напряжения 0…28 В с постоян-

ной времени L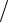( RL + RS3). После окончания импульса транзистор резко за-

пирается (ключ размыкается) и вся энергия, накопленная в индуктивности, идет на зарядку конденсатора С. В контуре возникает затухающий колебательный процесс, по частоте и амплитуде которого можно вычислить индуктивность дросселя и накопленную в нем энергию.

6. Подключить осциллограф между точками Cx и Rx. Установить по-

тенциометр R1 в положение, обеспечивающее подачу на контур минимального напряжения питания. Включить питание стенда и, увеличивая напряжение на выходе 0…+28 В, убедиться в появлении на входе осциллографа периодических затухающих колебаний. Измерить с помощью осциллографа период и

30