sb000008

30

− sin ϕ − sin(ϕ + θ) . ωCθ

Когда угол ϕ равен нулю, сопротивление R пропорционально отноше-

нию (1 – cos θ)/θ, которое всегда больше или равно нулю. Поэтому отрицательное сопротивление не может быть получено только за счёт пролётного эффекта. Однако при ϕ ≠ 0 сопротивление может стать отрицательным при некоторых значениях пролётных углов: при ϕ = π/2 наибольшее отрицатель-

ное сопротивление соответствует углу пролёта θ ≈ 3π/2.

Описанный принцип лежит в основе работы инжекционно-пролётного диода: инжекция неосновных носителей через барьер вносит запаздывание 90°, а пролётный угол, равный 270°, позволяет оптимизировать характеристики прибора.

Если ϕ = π, сопротивление максимально при θ = π. Эта ситуация реализуется в лавинно-пролётном диоде, в котором фазовый сдвиг 180° достигается за счёт конечного времени нарастания лавинного тока, а пролётный эффект приводит к добавочному запаздыванию на 180°.

Таким образом, проблема создания прибора, использующего при работе пролётные эффекты, сводится к поиску способа, с помощью которого можно вызвать запаздывание инжекции носителей в область дрейфа. При этом оче-

видно, что сумма инжекционной фазы и оптимального угла пролёта ϕ + θopt

приблизительно равна 2π, а отрицательное сопротивление растет по мере то-

го, как ϕ становится все более положительным. Из-за более высокого сопро-

тивления лавинно-пролётные диоды имеют лучшие КПД и генерируют большие мощности по сравнению с инжекционно-пролётными диодами.

Анализ работы в режиме малого сигнала. Для анализа работы ЛПД можно рассмотреть три области: 1) область лавинного умножения, размеры которой настолько малы, что ее объёмный заряд и время запаздывания сигнала можно не учитывать; 2) область дрейфа, в которой отсутствует генерация носителей,

31

а имеющиеся носители движутся со скоростями насыщения; 3) пассивную область, которая вносит нежелательное паразитное сопротивление.

Две активные области взаимодействуют друг с другом, так как переменное электрическое поле непрерывно на границе между ними. Плотность ла-

винного тока в области умножения JA равна плотности переменного тока проводимости в этой области. В области дрейфа плотность переменного тока проводимости представляет собой незатухающую волну, в которой изменяется лишь фаза, которая распространяется со скоростью движения носителей,

т. е. со скоростью насыщения vs:

где γ = JA 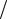J – комплексная величина, равная отношению плотности лавин-

ного тока к плотности полного тока.

В любом поперечном сечении плотность полного тока J равна сумме

откуда с учётом (6.1) – (6.3) получается выражение для переменной составляющей напряжённости электрического поля в области дрейфа, как функции x и J:

E(x) = J 1 − γe−iωxvs . iωεs

В предположении, что коэффициенты ионизации и скорости насыщения для электронов и дырок равны и дрейфовые токи во много раз больше диффузионных, в одномерном приближении работа ЛПД описывается следующими уравнениями:

32

В уравнениях непрерывности для электронов (6.7) и дырок (6.8) в правых частях с помощью вторых слагаемых учитываются процессы генерации электронно-дырочных пар за счёт лавинного умножения, которое во много раз превосходит тепловую генерацию, которая поэтому не учитывается во-

все. Суммирование (6.7) и (6.8), а затем интегрирование этой суммы по x от 0

до xA позволяет получить

где τA = xA 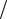vs – время пролета носителями области умножения. Поскольку при x = 0 ток электронов равен обратному току насыщения Jns, получается граничное условие Jp − Jn = −2Jn + J = −2Jns + J . Аналогично для плоско-

сти x = xA дырочный ток равен обратному току насыщения Jps генерируемых в области пространственного заряда дырок. Поэтому второе граничное усло-

вие имеет вид Jp − Jn = 2Jp − J = 2Jps − J . С учётом этих условий уравне-

ние (6.10) принимает вид

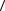где α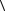 – средний коэффициент ионизации, равный интегралу по области ум-

ножения, а во-вторых, представить этот средний коэффициент ионизации, плотность тока и напряжённость поля в виде

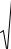
33

В результате подстановки этих соотношений в (6.12) получается выражение для переменной составляющей плотности лавинного тока проводимости

которая изменяется обратно пропорционально частоте, как в индуктивности. Ток смещения в области умножения равен

~Ad = ωεs ~A

J i E

и изменяется прямопропорционально частоте, т. е. имеет ёмкостный характер.

Таким образом, область умножения эквивалентна цепи, в которой ёмкость и индуктивность соединены параллельно, их значения определяются равенствами

LA = τA 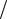2J0α′A , CA = εs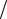AxA ,

а резонансная частота равна

Анализ работы в режиме большого сигнала. Область лавинного умножения с высоким электрическим полем, которое генерирует электронно-дырочные пары, расположена вблизи p+– n-перехода, а слаболегированный ν-слой обра-

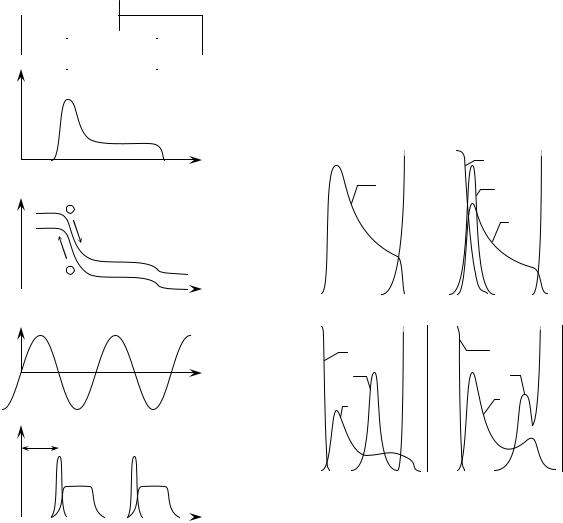
зует область дрейфа с практически однородным полем. Генерируемые дырки быстро попадают в p+-область, а генерируемые электроны инжектируются в область дрейфа, где совершают работу, равную выделяемой СВЧ-мощности. При периодических колебаниях электрического поля относительно среднего значения коэффициент ионизации, отнесенный к числу носителей заряда, практически мгновенно отслеживает колебания поля. Однако концентрация носителей не повторяет изменения поля, так как генерация зависит от числа уже имеющихся носителей. Даже после того, как поле достигнет максимального значения, концентрация носителей продолжает возрастать, поскольку скорость генерации все еще превышает среднее значение. В результате максимальным значение концентрации оказывается в тот момент, когда поле уменьшается приблизительно до своего среднего значения. Это означает, что изменение концентрации инжектированных носителей вместе с инжекционным током запаздывает по отношению к переменному напряжению (лавин-

34

ное запаздывание) почти на 90° даже тогда, когда коэффициент ионизации изменяется в фазе с полем (рис. 6.3, д). Максимум переменного электриче-

ского поля соответствует фазе π/2, а наибольшая концентрация инжектиро-

ванных носителей – фазе π. Инжектированные носители затем попадают в

Детализированные характеристики диода в режиме большого сигнала можно получить с помощью соотношений (6.4) – ( 6.9) и приближенных граничных условий. Рассчитанные зависимости электрического поля и концен-

траций электронов и дырок от расстояния x в обеднённой области кремниевого p+– n– ν– n+-диода при N1 = 1016 см–3 , N2 = 1015 см–3 , b = 1 мкм и W = 6 мкм с интервалом в четверть периода, приведены на рис. 6.4.

35

Генерация электронов и дырок начинается при максимальном напряжении, а через четверть периода импульсы заряда уже полностью сформированы и движутся через соответствующие области дрейфа. Дырки быстро покидают активную область, тогда как электроны дрейфуют приблизительно в течение полупериода, индуцируя положительной ток проводимости при отрицательном напряжении. За последующую четверть периода оставшиеся электроны выносятся из активной области, так как напряжение снова приближается к максимальному значению. Ток смещения достаточно большой и поло-

жительный (соответствует положительному смещению p+-контакта), в то время как напряжение на зажимах диода отрицательно. Амплитуда модуляции напряжения и тока велика, а эффективность высокая, если область лавинного умножения достаточно широкая.

Результаты расчётов показывают, что КПД может достигать 18 %.

6.2.Программа работы и указания по ее выполнению

1.По заданию, выданному преподавателем, построить профиль легирования однопролётного ЛПД.

2.Для напряжения на диоде, меняющегося с частотой, близкой к пролётной, рассчитать зависимость наведённого тока ЛПД от времени.

3.Рассчитать зависимости вещественной и мнимой составляющих проводимости ЛПД от частоты для разных значений амплитуды напряжения.

4.По заданию, выданному преподавателем, построить профиль легирования двухпролётного ЛПД.

36

5.Для напряжения на диоде, меняющегося с частотой близкой к пролётной, рассчитать зависимость наведенного тока ЛПД от времени.

6.Рассчитать зависимости вещественной и мнимой составляющих проводимости ЛПД от частоты для разных значений амплитуды напряжения.

Список рекомендованной литературы

Зи С. М. Физика полупроводниковых приборов: В 2 т./ Пер. с англ. М.:

Мир, 1984.

Зенкевич О., Морган К. Конечные элементы и аппроксимация. М.: Мир, 1986.

Кельман В. М., Явор С. Я. Электронная оптика. М.– Л.: Изд-во АН

СССР, 1963.

Ортега Дж., Пул У. Введение в численные методы решения дифференциальных уравнений. М.: Наука, 1986.

Хемминг Р. В. Численные методы. М.: Наука, 1968.

Хокни Р., Иствуд Дж. Численное моделирование методом частиц. М.:

Мир, 1987.

38

ASCII. Для просмотра входного файла следует использовать программу БЛОКНОТ (NOTEPAD), для просмотра выходного файла – приложение WordPad.

Подготовка входного файла и описание входного языка программы dd07001.DLL. Пример файла исходных данных приведен в прил. 2.

Символы входного языка – это символы ASCII. Используются ТОЛЬКО латинские символы на ВЕРХНЕМ регистре. Слова входного языка могут быть трех типов: число целого типа, например, 101 или число вещественного типа, например, 101.0 или 101.Е-8, или текст. Текстовое слово может быть командой или просто информацией.

Слова составляют предложение, которое всегда заканчивается символом “ <”. Предложение может быть расположено как на одной строке, так и на нескольких строках до символа “ <”. Строка содержит не более 80 символов. Строка является предложением или его частью, только если первый не пустой символ строки находится в позиции от 0 до 10. Иначе такая строка распознается как комментарий и не обрабатывается. Это позволяет вводить поясняющий текст, сдвинув его начало в 11-ю позицию, а также иметь в задаче альтернативные входные данные, сдвинув начало временно не используемых данных в 11-ю позицию.

Предложения, начинающиеся с командного слова, разделяют данные на блоки данных.

GRID – блок описания пространственной сетки. Параметр Kuzl – количество узлов сетки, Kzone – число областей, внутри которых шаг сетки постоянен и определяется как (Xn – Xn–1)/Kstepn . Если Kzone = 0, то координаты узлов сетки задаются массивом с числом элементов, равным Kuzl. При этом первое значение равно 0, а последнее – полной длине моделируемой структуры.

GEOMETRY – блок задания геометрических размеров. W(mkm) – полная длина моделируемой структуры, Xme(mkm) = 0.100 – толщина металлизации (контакта). Используется только для исследования катодолюминесценции.

DOPING CONCENTRATION – блок задания распределения концентрации ионизированной примеси. Используется три способа задания профиля примеси. При задании способом INTERPOLATION профиль примеси линейно меняется от значения N1 при х = 0 до N2 при х = 52 мкм (в данном примере примесь постоянна 6·1014 см–3 ), а затем аналогично для х = 52 … 352 мкм. Отме-

39

тим, что таким способом можно задавать резкое скачкообразное изменение профиля примеси. При задании способом GAUSS часть профиля будет построена в виде гауссова распределения. При этом экстремум распределения будет постоянен и равен Nmax= 6·1019 см–3 между точками Xm1 – Xm2 и меняется по закону Гаусса вне этих точек, причем в точке Xpn = 2 мкм значение концентрации примеси будет для данного примера равняться 3·1018 см–3 . При задании способом TBL профиль примеси описывается таблицей, при этом константа TBL в управляющем предложении указывает количество значений (до 500), а сами значения координаты и примеси записываются в виде двух последовательных предложений. Эти три способа можно комбинировать, при этом результирующий профиль примеси будет результатом суммирования отдельных профилей. Для учёта эффекта неполной ионизации примеси предусмотрено предложение FULL DOPING 0<. Если управляющая константа не равна 0, то необходимо описать профиль полной примеси аналогично спосо-

бу TBL.

MATERIAL – блок задания параметров материала. В программе предусмотрена возможность расчёта кремниевых, арсенид-галлиевых и карбидкремниевых полупроводниковых приборов. Материал указывается признаком 1, 2 или 3 соответственно. Признак Aval = 0 включает или выключает эффект лавинной генерации. Коэффициенты kn = 1.000, kp = 1.000 менять не надо. Параметры, задаваемые в следующем предложении блока, относительная диэлектрическая проницаемость, собственная концентрация, ширина запрещённой зоны, коэффициенты для описания подвижности и удельная плотность материала.

RECOMBINATION – блок задания коэффициентов рекомбинации. Коэффициенты Tau1, Tau2, No, Age, Bi кусочно-постоянно меняются в области между соответствующими координатами, например Tau1 = 0.6 мкс для х = 0 … 1.8 мкм, и Tau1 = 0.3 мкс для х = 1.8 … 2.1 мкм. Количество таких областей определяет константа Krec.

HETEROZONE 0 – блок задания гетероструктуры. Если в этом предложении задано не нулевое количество гетерозон, то следующее предложение имеет вид X(mkm) Xal1 Xal2. Здесь Xal – доля алюминия в соединении GaAlAs. Изменение этого параметра вдоль координаты х задаётся кусочнолинейным аналогично заданию профиля легирования по способу

INTERPOLATION.