
sb000008
.pdf
20
мещение доменов, вызванное ОДП, делает ДГ эффективными приборами СВЧ-диапазона.
Одним из важнейших физических механизмов возникновения объёмного отрицательного дифференциального удельного сопротивления служит эффект междолинного перехода электрона, например в арсениде галлия. Случайная флюктуация концентрации свободных носителей в любой точке образца с объёмным отрицательным удельным сопротивлением приводит к моментальному возникновению пространственного заряда, значение которого растет по экспоненциальному закону.
В одномерном приближении уравнение непрерывности для электронов имеет вид
∂n − 1 ∂Jn = 0.
∂t q ∂x
Малое локальное отклонение концентрации основных носителей от од-
нородной равновесной концентрации n0 приводит к появлению пространст-
венного заряда плотностью n – n0. Уравнение Пуассона тогда принимает вид
∂E = |
q |
(n − n ), |
(5.1) |
|
|||
∂x |
εs |
|
|
|
0 |
|
|
где εs – диэлектрическая проницаемость, а выражение для плотности тока
J= E − qD ∂n ,
ρ∂x
где ρ – удельное сопротивление; D – коэффициент диффузии. Продифферен-
цировав выражение для плотности тока по x и учитывая уравнение Пуассона, получим
|
1 ∂J |
|
n − n |
∂2n |
|
||||
|
|
|
|
|
= |
0 |
− D ∂x2 . |
|
|
|
q |
∂x |
ρεs |
|
|||||
Подстановка этого выражения в уравнение непрерывности, приводит к |
|||||||||
уравнению |
|
|
|
|
|
||||
∂n |
n − n |
∂2n |
|
||||||
∂t + |
|
0 |
− D ∂x2 = 0 |
, |
|||||
|
ρεs |
||||||||
которое можно решить методом разделения переменных. Если концентрация зависит только от координаты x, то решение можно представить в виде
n(x) = n0e−x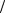 LD ,
LD ,

21
где n0 = n(0), а
LD = kTεs q2n0
– дебаевская длина, определяющая расстояние, на котором затухают малые флюктуации заряда. Если концентрация зависит только от времени, то реше-
ние уравнения имеет вид
n(t) = nt0 e−t τR ,
τR ,
где nt0= n(t = 0), τR = ρεs = εs 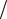 qμn ≈ εs
qμn ≈ εs 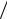 qμn0 – время диэлектрической релаксации, за которое происходит рассасывание пространственного заряда, если дифференциальное удельное сопротивление и дифференциальная удельная подвижность положительны. Однако в полупроводнике с отрицательным дифференциальным сопротивлением любая флюктуация концентрации будет нарастать по экспоненциальному закону:
qμn0 – время диэлектрической релаксации, за которое происходит рассасывание пространственного заряда, если дифференциальное удельное сопротивление и дифференциальная удельная подвижность положительны. Однако в полупроводнике с отрицательным дифференциальным сопротивлением любая флюктуация концентрации будет нарастать по экспоненциальному закону:
n(t) = nt0 et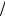
 τR .
τR .
При этом максимальная концентрация будет определяться временем пролета слоя пространственного заряда через прибор
nmax = nt0 eL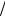 v τR .
v τR .
Очевидно, что для существенного увеличения заряда необходимо вы-
полнение условия L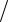 v τR > 1 или
v τR > 1 или
n0L > εsv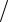 q μ− .
q μ− .
Для арсенида галлия правая часть имеет порядок 1012 см–2 . Это означает, что границей, разделяющей режимы работы приборов на эффекте ОДП, является величина произведения концентрации носителей на длину прибора, равная n0L = 1012 см–2 .
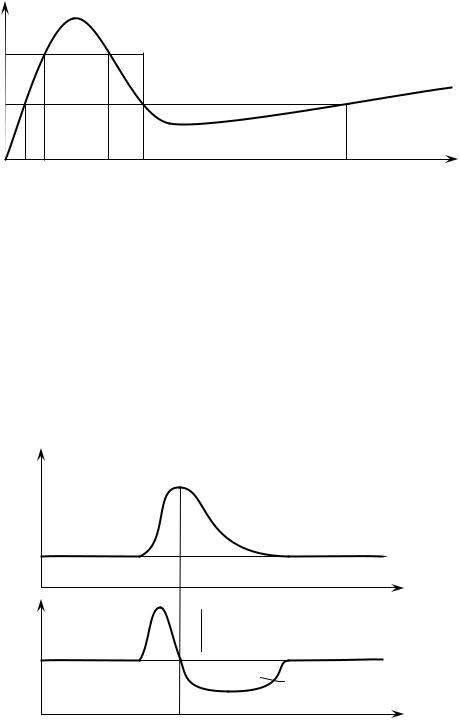
Если произведение n0L > 1012 см–2 , то вблизи катодного контакта, где флюктуации концентрации примеси и объёмного заряда максимальны, происходит формирование доменов, которые затем движутся к аноду. Процесс формирования домена в приборе с S-образной характеристикой (рис. 5.1, а) происходит следующим образом. Если из-за неоднородностей легирования или случайных шумов в некоторой точке A вблизи катода образовался избыток отрицательного заряда (рис. 5.1, б), распределение электрического поля (рис. 5.1, в), полученное в результате интегрирования уравнения Пуассона,
22
таково, что поле слева от точки A меньше, чем справа. Но тогда в соответствии с графиком ВАХ получается, что ток, втекающий в область вблизи точки
A, больше тока, вытекающего из нее, что приводит к накоплению пространственного заряда и увеличению разности электрического поля слева и справа от точки A. Этот процесс продолжается до тех пор, пока значения поля слева и справа от точки A не станут равными, соответственно, E1 и E2 (рис. 5.1, а),
J
|
E1 |
|
|
EA EA' |
E2 |
|
E |
|
|
|
|
EA— EA+ |
a |
|
|
|
|
|
|
|
|
|
|
– |
|
|
|
|
|
+ |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
xA |
б |
L |
x |
E |
|
|
|
|
|
|
|
|
EA+
EA
EA—
0xA
v
t1 t2
в |
L |
x |
t3
|
|
|
t1<t2<t3 |
|
|
|
|
|
|
|
|
|
|
0 |
xA |
г |
L |
x |
||
|
|
|
|
|
|
|
Рис. 5.1. Формирование домена в диоде Ганна
при которых J1 = J2. В результате образуется слой с повышенной концентрацией пространственного заряда, который движется вдоль образца под действием постоянного приложенного поля.
23
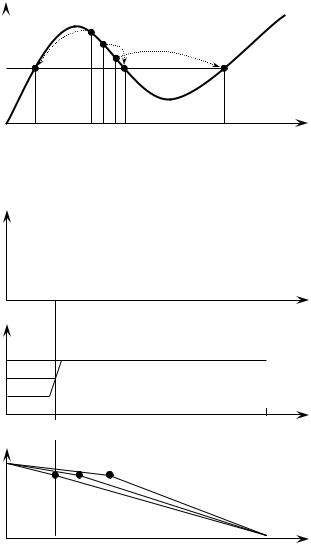
Скорость дрейфа электронов подчиняется статической зависимости, приведённой на рис. 5.2. Система уравнений, описывающих поведение элек-
v
vr
vrm
Erm Er |
Ee EDOM |
Em |
E |
Рис. 5.2. Зависимость скорости от напряженности электрического поля
тронов, состоит из уравнения Пуассона (5.1) и уравнения для плотности полного тока
J = qnv(E) − q |
∂D(E)n + ε |
∂E . |
(5.2) |
|
∂x |
s ∂t |
|
Вне домена концентрация носителей равна n0, а напряжённость поля –
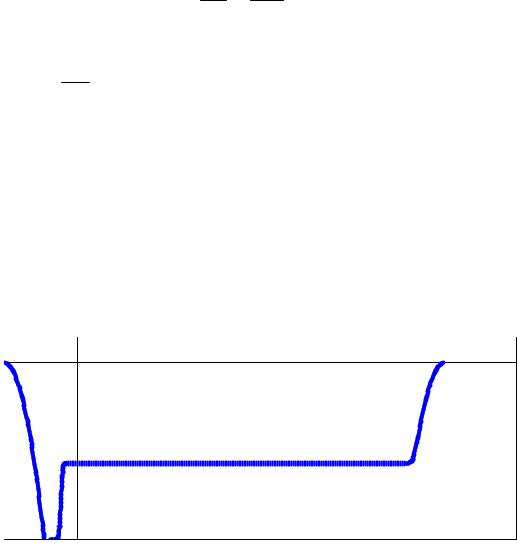
Er. Тогда решение этого уравнения должно иметь вид домена, движущегося со скоростью vDOM без изменения формы, и может быть представлено в виде
E
EDOM 
Er
n |
L |
|
 Обогащенный
Обогащенный
слой (n < n0)
n0
|
Обедненный |
|
слой (n > n0) |
x — vDOMt |
L |
функций, зависящих только от одной переменной x′ = x − vdomt :
Рис. 5.3. Распределения электрического поля и концентрации электронов для стабильного домена.
24
Ток вне домена состоит только из тока проводимости и определяется выражением J = qn0vr (E). Поскольку
∂E = |
∂E |
и |
∂E = −v |
∂E |
, |
|
∂x′ |
|
|||||
∂x |
|
∂t |
dom ∂x′ |
|
||
выражения (5.1) и (5.2) можно записать следующим образом:
∂E = q n
∂x′ εs
и
d ′ [D(E)n] = n[v(E) − vdom ] − n0(vr − vdom ). dx
При делении одного выражения на другое получается дифференциаль-
ное уравнение для [D(E)n] как функции электрического поля
q |
|
d |
[D(E)n] = |
n[v(E) − vdom ] − n0(vr − vdom ) |
. |
εs |
|
|
|||
|
dE |
|
n |
||
Для решения этого уравнения с учётом полевой зависимости коэффициента диффузии применяются численные методы.
5.2. Программа работы и указания по ее выполнению
p, см– 3
109
108
107
106
105
104
103
102
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
|
|
|
|
x , мкм |
|
|
|
Рис. 5.4. Распределение концентрации примеси в структуре диода Ганна
1.По заданию, выданному преподавателем, построить профиль легирования диода Ганна.
2.По заданной длине диода определить субкритический уровень легирования и рассчитать ВАХ. Определить суперкритическое легирование и
рассчитать ВАХ.
|
|
|
|
|
|
|
|
25 |
|
3. Рассчитать напряжение, при котором наблюдается генерация для |
|||||||
суперкритически легированного диода. Оценить частоту генерации. |
|
|||||||
|
900 нс |
|
915 нс |
930 нс |
960 нс |
985 нс |
945 нс |
|
|
10 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x , мкм |
|
/см |
0 |
|
|
|
|
|
|
|
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
|
кВ |
–5 |
|
|
|
|
|
|
|
E, |
|
|
|
|
|
|
|
|
|
–10 |
|
|
|
|
|
|
|
|
–15 |
|
|
|
|
|
|
|
|
–20 |
|
|
|
|
|
|
|
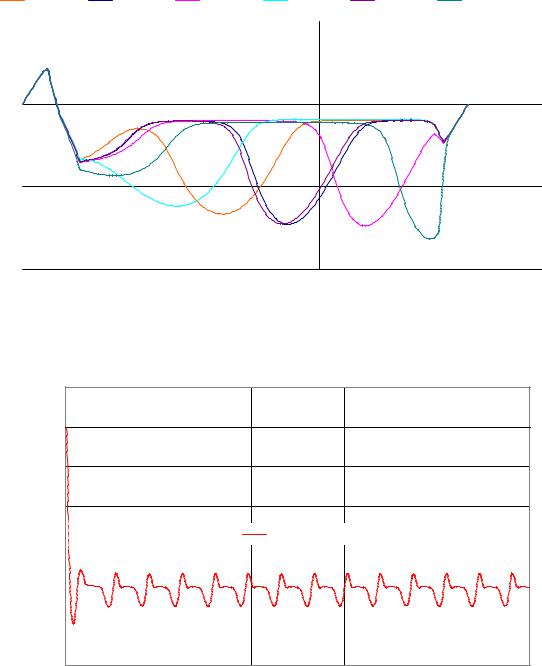
Рис. 5.5. Распределение напряженности поля в диоде Ганна в разные моменты времени
4. Ввести катодную затравку и проанализировать изменения процесса
генерации.
|
500 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0,0 |
0,2 |
0,4 |
0,6 |
0,8 |
t, нс 1,0 |
|
–500 |
|
|
|
|
|
– 2 |
|
|
|
|
|
|
см |
–1000 |
|
|
|
|
|
А/ |
|
|
|
INAB(A) |
|
|
, |
|
|
|
|
|
|
нав –1500 |
|
|
|
|
||
|
|
|
|
|
||
J |
|
|
|
|
|
|
|
–2000 |
|
|
|
|
|
|
–2500 |
|
|
|
|
|
|
–3000 |
|
|
|
|
|
|
Рис. 5.6. Генерация в диоде Ганна при включении на перепад напряжения |
|||||
5.Рассчитать импеданс суперкритически легированного диода Ганна
взависимости от частоты и амплитуды внешнего напряжения.
26
6. Исследование лавинно-пролетного диода
Цель работы – исследование физических процессов, определяющих свойства одно- и двухпролетных лавинных диодов (ЛД).
6.1. Основные теоретические положения
ЛД СВЧ-диапазона используется в качестве активного элемента генераторов и усилителей. Деление прибора на область лавинной генерации и область дрейфа позволяет наглядно изучить влияние пролетных эффектов, что важно для понимания принципов работы многих СВЧ-приборов.
Принцип работы лавинно-пролетных диодов основан на возникновении отрицательного сопротивления в диапазоне сверхвысоких частот, которое обусловлено процессами лавинного умножения носителей и их пролета через полупроводниковую структуру. Появление отрицательного сопротивления связано с запаздыванием по времени этих процессов, что приводит к фазовому сдвигу между током и напряжением. Запаздывание лавинного процесса обусловлено конечным временем нарастания лавинного тока, а так называемое пролетное запаздывание происходит за счёт конечного времени прохождения носителями области дрейфа. Если суммарное время этих запаздываний оказывается равным полупериоду колебаний, то сопротивление диода на данной частоте становится отрицательным.
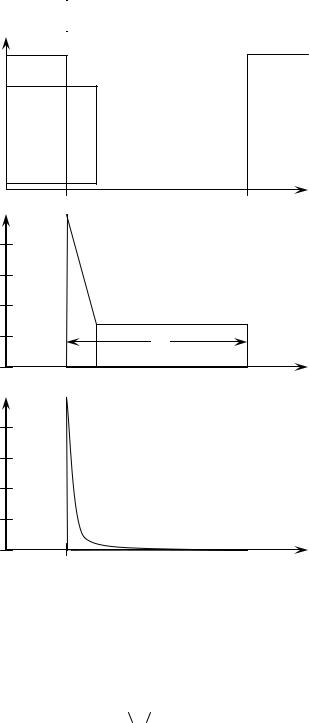
Основными представителями лавинно-пролетных диодов являются диод Рида (рис. 6.1), асимметричный резкий p– n-переход, симметричный p– n- переход (диод с двумя дрейфовыми областями), диод с двухслойной базой,
диод с трехслойой базой (модифицированный диод Рида) и p– i– n-диод. Поскольку коэффициент ударной ионизации сильно зависит от напря-
жённости электрического поля, процесс лавинного умножения носителей происходит в очень узкой области от 0 до xA, называемой областью лавинного умножения, в которой напряжённость поля имеет значение более 150 кВ. Слой за пределами этой области называется областью дрейфа.
Если область с концентрацией N2 отсутствует, то получается диод с рез-
ким асимметричным p– n-переходом (рис. 6.2). Если же отсутствует область с концентрацией N1, то диод Рида вырождается в p– i– n-диод.
27
в идеальном p– i– n-диоде занимает всю ши-
рину слоя собственной концентрации. В диодах Рида и p– n-переходах эта область очень узкая и расположена вблизи металлургической границы пере-
хода. В этом случае ширина области умножения xA определяется таким обра-
1020
3– 16
см 10
|N D N– A |,
1013
5 |
4 |
|
2 |
||
/смВ·10 |
||
|
3 |
|
E, |
1 |
|
|
||
|
0 |
|
4 |
8 |
|
·10 |
6 |
|
1 |
||
– |
|
|
, см |
4 |
|
<α> |
2 |
|
|
||
|
0 |
p+ |
n |
i |
n+ |
|
|
|
|
N1
N2
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
1 |
2 |
3 |
x, мкм |
|||||
W
|
|
|
|
|
|
|
|
0 b 1 |
2 |
3 |
x, мкм |
||||
|
|
|
|
|
|
|
1 |
2 |
3 |
x, мкм |
|||
Рис. 6.1. Распределение примесей и напряжённости электрического поля при пробое в p+– n– i– n+-диоде Рида
зом, чтобы при интегрировании эффективного коэффициента ионизации от 0
до xA получить не менее 95 %:
xA
∫ 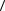 α
α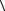 dx = 0,95 ,
dx = 0,95 ,
0
а для диода Рида, диода с двухслойной базой, асимметричного резкого
28
p+– n-перехода и симметричных p– n-переходов при пробое
xA
2
∫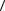 α
α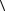 dx = 0,95.
dx = 0,95.
−xA
2
совпадает с обеднённой областью, за исключением слоя лавинного умножения носителей, т.е. xA ≤ xd ≤ W . Время пролета области дрейфа определяется скоростью дрейфа, которая определяется достаточно большой напряжённостью электрического поля и называется скоростью на-
сыщения vs. В кремнии значение напряжённости электрического поля должно превышать 104 В/см, в арсениде галлия – 10 3 В/см.
– 3 |
|
|
|
см |
10 |
20 |
|
, |
|||
|
|||
Концентрация |
1016 |
||
|
|||
5 |
4 |
||
см·10 |
3 |
||
|
|||
В/ |
2 |
||
E, |
1 |
||
|
|||
|
0 |
||
4 |
|
|
|
·10 |
8 |
||
– 1 |
|
|
|
,см |
6 |
||
|
|||
<α> |
4 |
||
2 |
|||
|
|||
|
0 |
||
|
|
p+ |
|
|
|
|
n |
|
|
n+ |
|
3 |
|
|
|
p+ |
|
p |
|
|
|
n |
|
|
n+ |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, см |
1020 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
p+ |
|
|
|
|
|
|
|
|
n+ |
Концентрация |
|
|
|
p |
+ |
|
|
|
|
|
|
|
|
|
+ |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
n |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
1016 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
x, мкм |
|
|
|
|
|
0 |
1 |
|
2 |
3 x, мкм |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
4 |
|
|
|
|
|
+ |
|
|
– |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
см·10 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
+ |
|
|
|
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E, В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
xA |
|
|
|
|
|
|
|
|
|
—W/2 |
|
|
|
|
|
|
|
W/2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x, мкм |
|
|
0 |
1 |
2 |
3 |
x, мкм |
|
|
|
|
|
|
—xA/2 |
|
xA/2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
·10 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– 1 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
, см |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
<α> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
x, мкм |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
x, мкм |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Рис. 6.2. Распределение примесей, напряжённости электрического поля и эффективного коэффициента ионизации в диоде с резким
p+– n-переходом и в p+– p– n– n+-диоде с симметричным резким p– n-переходом (диод с двумя дрейфовыми областями – двухпролётный ЛПД)

29
Поскольку в диоде Рида минимальная напряжённость электрического поля в области дрейфа имеет вид
E |
|
= E − |
q |
[N b + N (W − b)], |
|
min |
ε0 |
||||
|
m |
1 2 |
|||
|
|
|
|
параметры диода Рида должны определяться из условия Emin > Es, соответст-
вующего скорости vs.
В резких p– n-переходах всегда существуют области, в которых напряжённость электрического поля меньше необходимой для пробоя. Однако отношение ширины такой области с напряжённостью меньше 104 В/см в крем-
ниевом p+– n-переходе с концентрацией примеси 1016 см–3 к полной ширине обеднённой области, в начале которой напряжённость поля равна в данном случае 4·105 В/см, составляет всего 104/4·105 = 2,5 %. Поэтому существование областей слабого поля практически не сказывается на времени пролета носителей через обеднённую область.
6.1.1 Динамические характеристики
Предположим, что импульс тока проводимости инжектируется при x = 0 с фазовым углом ϕ по отношению к полному току, а приложенное к диоду постоянное смещение таково, что инжектированные носители заряда пролетают область дрейфа со скоростью насыщения vs. Плотность переменного тока проводимости Jc при x = 0 равна полной плотности тока J со сдвигом по фазе
J0c = Jc(0) = J exp(− iϕ).
В произвольной точке области дрейфа полный переменный ток равен сумме тока проводимости и тока смещения:
J(x) = Jc(x) + Jd (x) = J0ce−iωx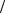 vs + iωεsE(x),
vs + iωεsE(x),
где E(x) – переменная составляющая напряжённости электрического поля. Учитывая два предыдущих выражения, получаем
E(x) = J(1 − e−iωx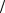 vs −iϕ ).
vs −iϕ ).
Значение импеданса диода получим путём интегрирования
