
sb000008
.pdf
Федеральное агентство по образованию
Санкт-Петербургский государственный электротехнический университет “ ЛЭТИ”
Б. В. ИВАНОВ А. Е. СИНЕВ
КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ И ПРОЕКТИРОВАНИЕ ЭЛЕКТРОННЫХ ПРИБОРОВ
Санкт-Петербург
2007

Федеральное агентство по образованию
Санкт-Петербургский государственный электротехнический университет “ ЛЭТИ”
Б. В. ИВАНОВ А. Е. СИНЕВ
КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ И ПРОЕКТИРОВАНИЕ ЭЛЕКТРОННЫХ ПРИБОРОВ
Лабораторный практикум
Санкт-Петербург Издательство СПбГЭТУ “ ЛЭТИ”
2007
УДК 621.38.63(07)
ББК З 85я7 + Ж.с11я7
И 76
Иванов Б. В., Синев А. Е.
И 76 Компьютерное моделирование и проектирование электронных приборов: Лабораторный практикум. СПб.: Изд-во СПбГЭТУ “ ЛЭТИ”, 2007. 48 с.
ISBN 5–7629–0865–8
Кратко рассмотрены вопросы математического моделирования и методика компьютерного моделирования основных физических процессов в электронных приборах.
Предназначено для студентов, обучающихся по направлению 550700 “ Электроника и микроэлектроника” и по специальности 200300 “ Электронные приборы и устройства”.
УДК 621.38.63(07)
ББК З 85я7 + Ж.с11я7
Рецензенты: кафедра физической электроники радиофизического факультета СПбГТУ, канд. техн. наук Ю. Н. Зуев (НИИЭФА им. Ефремова).
Утверждено редакционно-издательским советом университета
в качестве учебного пособия
ISBN 5–7629–0865–8 |
© СПбГЭТУ “ ЛЭТИ”, 2007 |
3
Введение
Полный цикл моделирования полупроводниковых приборов можно условно разделить на две части: моделирование технологических процессов и расчёт характеристик приборов с заданным диффузионным профилем.
Для описания процессов изготовления приборов используются различные модели, такие как модель диффузии при окислении или модель ионной имплантации. Нестационарное уравнение, описывающее диффузию окислителя, например, Si3N4 в SiO2, имеет вид
¶C = div(D grad C),
∂t
где C – концентрация окислителя; D – коэффициент диффузии.
В процессе моделирования полупроводниковых электронных приборов необходимо решить фундаментальную систему уравнений (ФСУ) относи-
тельно распределения плотностей электронов – n и дырок – |
p, а также рас- |
|||||||
пределения потенциала ϕ: |
|
|
|
|
|
|
|
|
Jn = qmnnE + qDnÑn ; |
(В.1) |
|||||||
Jp = qmppE - qDpÑp; |
(В.2) |
|||||||
¶n = |
ÑJn + (G |
n |
− R ); |
(В.3) |
||||
∂t |
|
q |
n |
|
||||
|
|
|
|
|
||||
¶p = - |
ÑJp |
+ (G |
|
- R ); |
(В.4) |
|||
|
|
p |
||||||
¶t |
|
|
q |
|
p |
|
||
|
|
|
|
|
|
|||
Ñ(eÑj) = |
q |
(n - p + NA− - ND+ ). |
(В.5) |
|||||
|
||||||||
|
e0 |
|
|
|
|
|||
В уравнениях (В.1) и (В.2) плотности электронного и дырочного токов, состоящие из дрейфового (полевого) и диффузионного (обусловленного градиентом концентрации) компонентов, зависят от подвижностей электронов mn и дырок mp и коэффициентов диффузии для электронов Dn и дырок Dp, которые, в свою очередь, определяются значениями подвижностей и температуры через соотношения Эйнштейна Dn=(kT/q)mn и Dp=(kT/q)mp.
В уравнениях непрерывности для электронной (В.3) и дырочной (В.4) составляющих тока Gn и Gp – скорости генерации электронов и дырок в единице объёма, а Rn и Rp – скорости рекомбинации электронов в p-области и дырок в n-области.
Подставив выражения для плотностей тока в уравнения непрерывности с учётом соотношений Эйнштейна, а также связи напряжённости электрического поля с потенциалом и приняв диэлектрическую проницаемость среды e константой, получим систему трех уравнений
∂n |
= -Ñ[m |
|
(nÑj - j Ñn)] + (G |
|
- R ); |
(В.6) |
|
n |
n |
||||
¶t |
T |
n |
|
|||
|
|
|
|
|
||
4
∂p |
= -Ñ[m |
|
(pÑj + j Ñp)]+ (G |
|
- R |
); |
(В.7) |
||
|
p |
p |
|||||||
¶t |
|
|
T |
p |
|
||||
|
|
|
(p - n + ND+ - NA− ). |
|
|
||||
|
Ñ2j = - |
q |
|
(В.8) |
|||||
|
|
|
|||||||
|
|
|
|
ee0 |
|
|
|
|
|
В эту систему помимо трех связанных друг с другом величин входят зависящие от этих же величин подвижности и скорости генерации и рекомбинации электронов и дырок, что делает невозможным решение данной системы в общем случае. На практике используются различные модели, учитывающие в большей или меньшей степени известные эффекты, зависимости и закономерности, связывающие параметры, входящие в ФСУ как между собой, так и с другими параметрами, характеризующими, например, материал прибора.
1.Моделирование профиля легирования
вдиодных и триодных структурах
Цель работы – изучение основных методов решения задачи диффузии примесей в полупроводниковые материалы и различных способов визуализации полученных результатов, а также анализ точности решения.
1.1.Основные теоретические положения
Внаиболее общем виде модель технологического процесса диффузии вещества должна учитывать температурные зависимости скорости диффузии, вязкость диффундирующего вещества и упругость материала подложки, определяющие деформацию подложки при диффузии в нее инородных атомов. Если же не учитывать деформацию материалов и считать независимым от температуры коэффициент диффузии D, то в двумерном приближении можно использовать уравнение
¶C(x, y, t) |
|
¶2C(x, y, t) |
+ |
¶2C(x, y, t) |
= Q(x, y, t), |
(1.1) |
|
¶t |
- D |
¶x2 |
¶y2 |
|
|||
|
|
|
|
|
|||
где С(x,y,t) – зависящая от координат и времени функция концентрации вещества; Q(x,y,t) – функция интенсивности источников вещества.
Уравнение (1.1) представляет собой параболическое уравнение, которое в общем случае не имеет аналитического решения. Однако численное решение можно получить при помощи широко распространенных пакетов про-
грамм, таких как Mathcad, Mathematica, MATLAB.
5
1.2. Решение двумерного уравнения диффузии методом конечных элементов в системе MATLAB 7.0
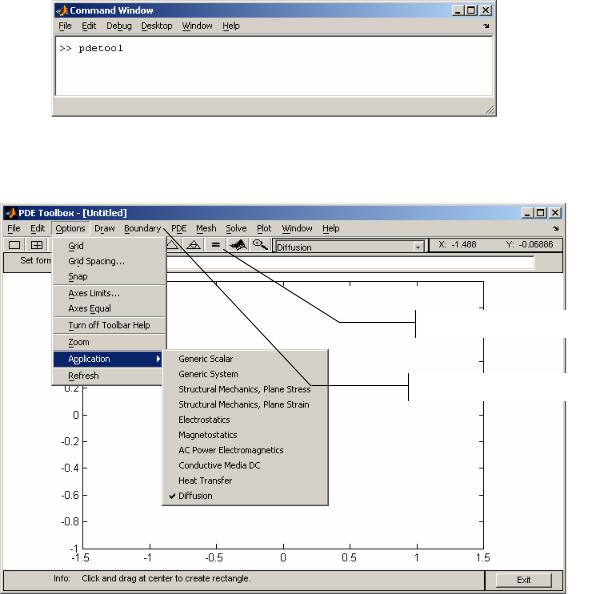
Для решения дифференциальных уравнений в частных производных методом конечных элементов в системе MATLAB используется приложение PDE Toolbox, которое запускается из командного окна MATLAB при помощи
команды pdetool:
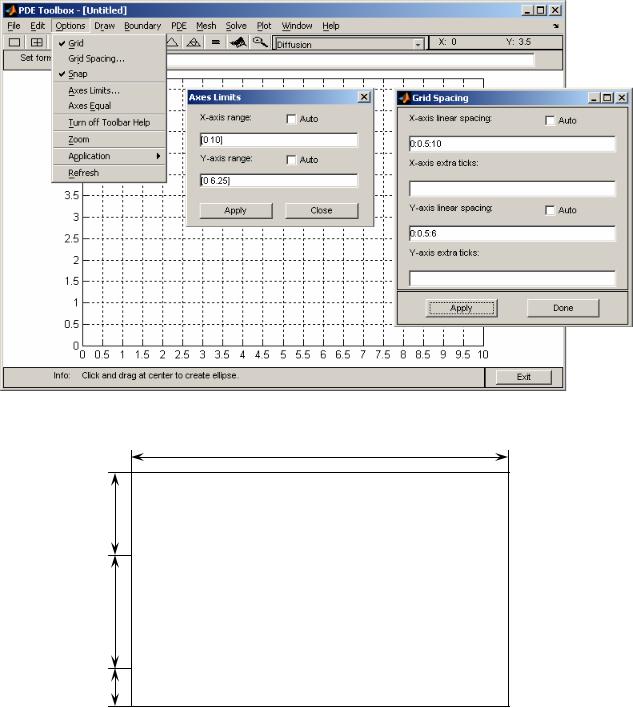
В открывшемся окне PDE Toolbox с помощью команды меню Options | Application из списка можно сразу выбрать тип решаемой задачи. При расчёте профиля легирования в полупроводниковых приборах используется приложение Diffusion:
Панель инструментов
Панель главного меню
Рабочая среда PDE Toolbox позволяет последовательно выполнять следующие этапы решения дифференциальных уравнений методом конечных элементов:
1)конструирование области из геометрических примитивов;
2)задание граничных условий;
3)триангуляцию расчётной области;
4)решение уравнения методом конечных элементов;
5)построение двумерных и трёхмерных графиков.
6
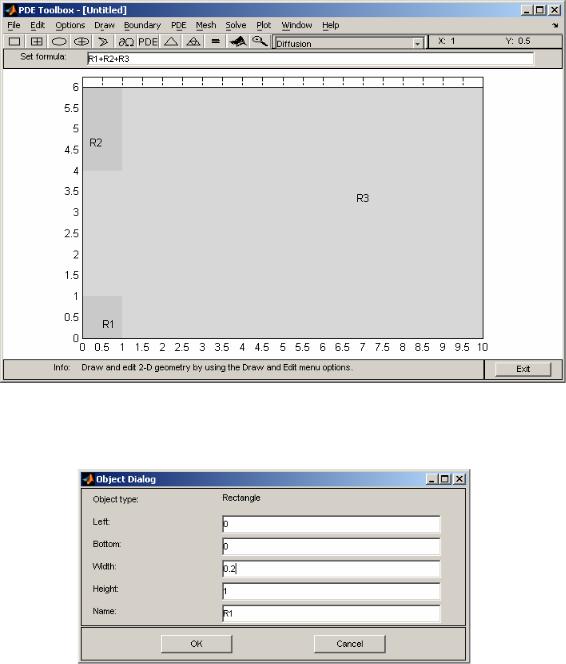
Построение расчётной области производится на сетке, размеры и густоту линий которой задают при помощи команд меню Options | Axes Limits… и
Options | Grid Spacing…:
Установка флажка Options | Grid делает сетку видимой, а флажок помогает задавать положение и размеры объектов в привязке к
10
B C
B1
A1
A D
Рис. 1.1. Схема расположения электродов в биполярном транзисторе
7
сеточным линиям при формировании расчётной области из примитивов типа прямоугольник, эллипс и полилиния. При этом можно использовать как пиктограммы, расположенные на панели инструментов, так и команды меню
Draw: Polygon, Rectangle/square, Rectangle/square (centered), Ellipse/circle, Ellipse/circle (centered).
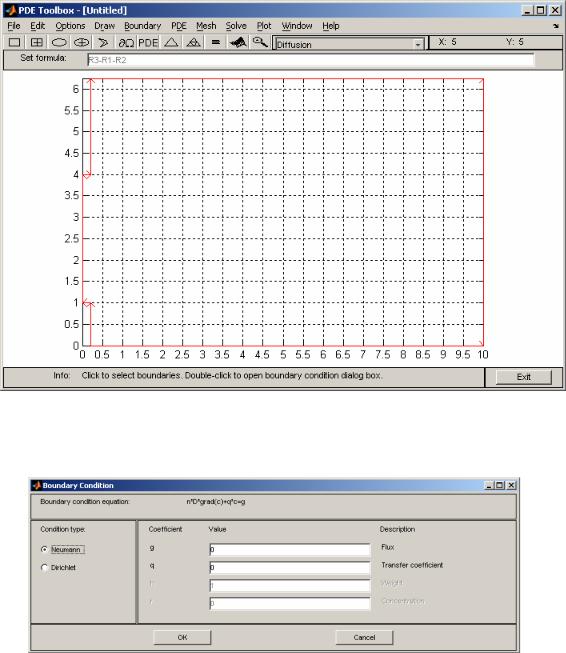
Для формирования области, размеры которой приведены на рис. 1.1, сначала рисуем три прямоугольника R1, R2, и R3 в режиме Options | Snap.
Для корректировки размеров прямоугольников используется панель Object Dialog, которая открывается при двойном щелчке мыши по выбранному объекту. Например, для прямоугольника R1 (имя объекта указано в нижнем поле редактирования) можно изменить ширину на значение 0.2.
Аналогичная процедура для остальных двух прямоугольников позволяет сформировать расчётную область в виде суммы R1+R2+R3, которая отображается в окне Set formula. Если прямоугольники R1 и R2 необходимо вычесть из R3, то формула должна содержать запись вида R3–R1–R2.
8
Для задания граничных условий используются команды меню Boundary, к которым можно перейти либо щелчком мыши по соответствующей кнопке в строке главного меню, либо нажав комбинацию клавиш Ctrl+B.
По умолчанию на всех границах задаётся граничное условие Дирихле с нулевыми значениями. В рассматриваемом примере на участках BC и AD используется симметрия, и потому выполняется однородное условие Неймана. На открытом участке A1B1 также задано однородное условие Неймана.
На границах AA1 и CD задаётся значение концентрации 1017 см–3 , а на границе BB1 – 2·10 15 см–3 .
Полагая правую часть (1.1) равной нулю (отсутствие источников), задают параметры дифференциального уравнения с частными производными с
помощью команды PDE | PDE Specification…
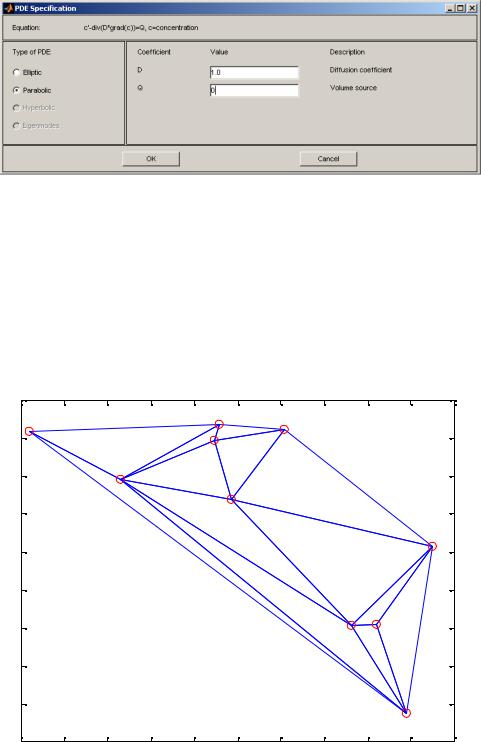
9
Последний подготовительный этап состоит в триангуляции – покрытии расчётной области сеткой, состоящей из треугольников, параметры которых определяются в меню Mesh. Процесс триангуляции автоматизирован и основан на методе Делоне, который позволяет строить треугольники таким образом, что описанная около каждого из треугольников окружность не содержит вершин соседних треугольников. Среди всех возможных произвольных триангуляций триангуляция Делоне обладает максимальной суммой минимальных углов всех своих треугольников, а также минимальной суммой радиусов окружностей, описанных около треугольников.
1 |
|
|
|
|
|
|
|
|
|
|
0.9 |
|
|
|
|
|
|
|
|
|
|
0.8 |
|
|
|
|
|
|
|
|
|
|
0.7 |
|
|
|
|
|
|
|
|
|
|
0.6 |
|
|
|
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
|
|
|
|
0.3 |
|
|
|
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
|
|
|
0.1 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
0 |
Самая грубая сетка может быть сгенерирована при использовании команды Mesh | Initialize Mesh, которая запускается либо при нажатии соответствующей кнопки с изображением треугольника на инструментальной панели (содержащей пиктограммы некоторых часто используемых команд), либо с помощью комбинации клавиш Ctrl+I.
