YzhR47Vwqa

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»

ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКИХ ПАКЕТОВ ДЛЯ РЕШЕНИЯ СТАТИСТИЧЕСКИХ ЗАДАЧ

Методические указания к типовым расчетам и тестированию

Санкт-Петербург Издательство СПбГЭТУ «ЛЭТИ»

2014

УДК 519.22(07)

Применение математических пакетов для решения статистических задач: метод. указания к типовым расчетам и тестированию / сост.: А. В. Морозова, А. В. Чирина. СПб.: Из-во СПбГЭТУ «ЛЭТИ», 2014. 32 с.

Включают следующие разделы: тесты по теории вероятностей; разбор варианта теста; варианты и указания к индивидуальным домашним заданиям по математической статистике. Содержат обзор основных формул по теории вероятностей и математической статистики. После краткого изложения основных положений теории рассмотрены типовые задания с подробными решениями.

Предназначены для студентов очной и заочной форм обучения. Для подготовки к тестированию и для выполнения студентами типового расчета по курсу «Теория вероятностей и математическая статистика. Дополнительные главы».

Утверждено редакционно-издательским советом университета

в качестве методических указаний

© СПбГЭТУ «ЛЭТИ», 2014

2

Раздел 1. ТЕОРИЯ ВЕРОЯТНОСТЕЙ

1.1. Классическая вероятность. Основные комбинаторные формулы

Формула классической вероятности предполагает, что все рассматрива-

емые элементарные события, образующие пространство элементарных со- бытий Ω, равновозможны. При этом допущении вероятность события A вычисляется по формуле

P( A) = k , n

где k – число элементов, благоприятствующих событию A , а n – число всех элементов Ω. Для нахождения числа благоприятных и возможных событий часто используют формулу числа всех перестановок элементов множества Ω: Pn = n! =1× 2 ×…× n. Удобно считать, что 0! = 1.

Число сочетаний из n по k – это количество всех k-элементных подмножеств n-элементного множества, или, иначе говоря, количество всех неупорядоченных наборов длиной k различных элементов n-элементного множества,

Число размещений без повторения из n по k – количество всех упорядоченных наборов длиной k различных элементов n-элементного множества:

Число размещений с повторением из n по k – количество всех упорядоченных наборов длиной k элементов n-элементного множества; при этом

набор может содержать повторяющиеся элементы ɶk = k

An n .

1.2. События и операции над ними

Пространство элементарных событий – это множество всех исходов экс-

перимента. Событие – подмножество пространства элементарных событий (более точное определение см. Гнеденко Б. В. Курс теории вероятностей. М., 1988).

Невозможное событие – событие, которому не благоприятствует ни один исход эксперимента. Вероятность невозможного события равна 0.

3

Достоверное событие – событие, которому благоприятствует любой исход эксперимента. Вероятность достоверного события равна 1.

Пусть A – событие. Тогда противоположным к нему событием назы-

вают событие, состоящее в том, что A не произойдет (обозначение: A ):

P ( A) = 1 − P( A).

Два события называют несовместными, если их пересечение пусто, т. е. они не могут произойти одновременно. Произвольное число событий называют несовместными, если любые два из них несовместны. Вероятность суммы (объединения) несовместных событий равна сумме их вероятностей.

1.3. Условные вероятности. Независимые события. Формулы сложения и умножения, формула включений-исключений

Если вероятность события B не равна нулю, то условной вероятностью

P ( A B), или вероятностью события A при условии B называют отношение

P ( A B) = P( A ∩ B) .

P(B)

Формула умножения вытекает непосредственно из определения:

P( A ∩ B) = P ( A B) × P(B).

События A и B называют независимыми, если P( A ∩ B) = P( A) × P(B). События называют попарно независимыми, если любые два из них неза-

висимы. События, входящие в некоторый набор событий, называют незави- симыми в совокупности, если вероятность пересечения произвольного поднабора событий равна пересечению вероятностей этих событий. Из независимости в совокупности вытекает попарная независимость; обратное в общем случае неверно!

Формула сложения: для произвольных событий A и B вероятность их суммы (т. е. того, что произойдет хотя бы одно из них), равна

P( A B) = P( A) + P(B) - P( A ∩ B) .

Для произвольного конечного объединения событий верна формула включений-исключений:

4

1.4. Формула полной вероятности. Формула Байеса

Представление пространства элементарных событий в виде суммы

n

несовместных событий Ω = Hi , P (Hi ∩ H j ) = Æ, "i ¹ j , называют разби-

i=1

ением, а события Hi – гипотезами. Если A – событие и Hi , i = 1, ..., n – гипо-

тезы, то верна формула полной вероятности:

n

P( A) = ∑ P ( A Hi )P (Hi ). i=1

Формула Байеса: если A – событие и Hi , i = 1, ..., n – гипотезы, то

j=1

1.5.Случайные величины и их характеристики

Функция распределения случайной величины X – такая функция F (x),

что для любого x выполняется равенство P( X < x) = F (x).

Функция распределения не убывает (нестрого возрастает) на всей вещественной прямой; F (−∞) = 0 , F (+∞) = 1. Если везде, за исключением конечного числа точек, существует f (x) = F′(x) , то величину X называют непре- рывной, а f (x) – плотностью случайной величины X . Плотность неотрица-

тельна при любых x и

∞

∫ f (x) dx =1.

−∞

Если случайная величина принимает лишь конечное или счетное количество значений, то ее называют дискретной.

Математическое ожидание непрерывной случайной величины X вычисляется по формуле

∞

EX = ∫ xf (x) dx.

−∞

Математическое ожидание дискретной случайной величины X вычисляется по формуле

EX = ∑ ai pi , где pi = P( X = ai ), i = 1, ..., n. i

5

Для любых случайных величин X и Y и любых чисел a и b E(aX + bY ) = aEX + bEY .

Если X и Y независимы, то EXY = EX × EY . Дисперсией случайной величины X называют

DX = E( X - EX )2 = EX 2 - (EX )2 .

Дисперсия всегда неотрицательна. Если дисперсия равна нулю, то случайная величина с вероятностью 1 равна константе. Дисперсия суммы независимых случайных величин равна сумме их дисперсий.

Ковариацией случайных величин X и Y называют

cov ( X ,Y ) = E (( X - EX )(Y - EY )) = EXY - EX × EY .

Из определений ясно, что DX = cov( X , X ) .

Коэффициентом корреляции случайных величин X и Y называют

ρ( X ,Y ) = cov( X ,Y ) .

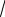DX × DY

Всегда ρ £1. Если ρ( X ,Y ) =1, то X и Y линейно зависимы.

Если X и Y – независимые случайные величины, то ρ( X ,Y ) = 0 . Обратное в общем случае неверно!

1.6. Характеристические функции случайных величин

Функцию φ(t) называют характеристической функцией (х. ф.) случай-

ной величины X , если φ(t) = E exp (itX ). Х. ф. определена t . Для

t φ(t) £1; φ(0) = 1.

Характеристическая функция суммы независимых случайных величин равна произведению их характеристических функций.

1.7. Образец экзаменационного билета по теории вероятностей

Задача 1. В одной упаковке было 10 тетрадей в клетку и пять в линейку, а в другой – восемь тетрадей в клетку и 12 в линейку. Из каждой упаковки вынули по две тетради. Найти вероятность того, что хотя бы одна из них – тетрадь в клетку.

Решение. Введем обозначения для следующих событий: A – вынули хо- тя бы одну тетрадь в клетку; A – противоположное к A : не вынули ни одной тетради в клетку, т. е. все вынутые тетради – в линейку; B1 – обе тетради,

6

взятые из первой упаковки, оказались в линейку; B2 – обе тетради, взятые из второй упаковки, оказались в линейку.

Событие, вероятность которого нужно найти, – это событие A . Будем вычислять его вероятность через вероятность противоположного события: P( A) =1 - P( A) . Так часто делают, когда в описании события есть слова «хотя бы один/одна/одно». Событие A можно представить в виде пересечения событий: A = B1∩B2 . События B1 и B2 независимы, т. е. вероятность их пересечения можно найти по формуле P(B1∩B2 ) = P(B1) × P(B2 ).

Для вычисления вероятностей событий B1 и B2 осталось воспользовать-

ся классическим определением вероятности, а также основными комбина-

торными формулами. Найдем, например, вероятность события B2 . Количество случаев, благоприятствующих событию B2, – это количе-

ство способов выбрать две тетради из 12, а число возможных случаев – это количество способов выбрать две тетради из 8 + 12 = 20. Вычислим его по формуле для числа сочетаний:

Ответ: 643 » 0.967. 665

Задача 2. Шесть одинаковых пирожных случайным образом разложили по трем тарелкам. Найти вероятность того, что на каждой тарелке есть хотя бы одно пирожное.

Решение. Это задача на применение формулы включений-исключений,

позволяющей вычислить вероятность суммы событий.

Переформулируем вопрос задачи: найти вероятность события A – ни одна тарелка не пуста. Противоположное к нему событие A – хотя бы одна

7

из тарелок пуста. Введем обозначения: B j – тарелка с номером j пуста (где j = 1, 2, 3). Тогда A = B1 B2 B3 . Формула включений-исключений для объединения трех множеств выглядит так:

P(B1 B2 B 3) = P(B1) + P(B2 ) + P(B3) − P(B1B2 ) −

− P(B1B3) − P(B2B 3) + P(B1B2B3) .

Очевидно, что вероятность события B1B2B3 «все тарелки пусты» равна нулю, так как это событие невозможно. Событие B1 состоит в том, что первая тарелка пуста, а значит, каждое из шести пирожных попало на одну из двух оставшихся тарелок. Для каждого пирожного вероятность попадания на две из трех тарелок равна 23. Пирожные раскладываются по тарелкам неза-

висимо друг от друга, поэтому P(B1) = (23)6 . Аналогично вычисляются вероятности событий B2 и B3 . Событие B1B2 состоит в том, что первая и вторая тарелки пусты, а значит, все пирожные находятся на третьей тарелке. Ве-

роятность этого события, очевидно, равна (1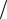3)6 . Точно так же вычисляются вероятности событий B2B3 и B1B3 . Окончательно получим:

Ответ: 20 » 0.74. 27

Задача 3. В мешке с яблоками находится 40 % зеленых, 25 % красных и 35 % желтых яблок. Вероятность поражения гнилью для зеленого яблока равна 0.1, для красного яблока – 0.3 и для желтого яблока – 0.2. Из мешка наугад вытащили яблоко, и оказалось, что оно гнилое. Какова вероятность того, что это яблоко было зеленым?

Решение. Введем гипотезы: H1 – выбранное яблоко было зеленым, H2 – красным и H3 – желтым. Обозначим буквой A событие: «выбранное яблоко гнилое». Запишем условие задачи в виде набора условных и безусловных вероятностей:

P(H1) = 0.40; P( A H1) = 0.1;

P(H2 ) = 0.25; P( A H2 ) = 0.3;

P(H3) = 0.35; P( A H3) = 0.2.

8

Надо вычислить условную вероятность P( A H1), т. е. вероятность того,

что яблоко было зеленым при условии, что оно оказалось гнилым. Применим формулу Байеса, которая в рассматриваемом случае выглядит так:

∑P(Hi )P( A Hi )

i=1

Подставим в формулу числовые значения:

Найти: а) EX и DX; б) плотность и функцию распределения случайной

величины Y= e−2 X .

Решение. а) Воспользуемся формулами для выражения математического ожидания и дисперсии через плотность распределения:

б) Случайная величина Y является строго убывающей функцией от X: Y = g( X ) , где g(x) = e−2x : [0,∞) (0,1], а обратная к ней функция выража-

9

Таким образом, случайная величина Y имеет равномерное распределение на интервале [0,1] . Ее функция распределения

Плотность распределения получается дифференцированием функции распределения.

Задача 5. Случайные величины X и Y независимы, и каждая из них имеет плотность f (x) из задачи 4. Найти плотность случайной величины X + Y.

Решение. Воспользуемся формулой свертки:

Пояснение. Произведение плотностей под интегралом не равно нулю тогда и только тогда, когда одновременно y > 0 и x − y > 0 .

Ответ: 4xe−2x , x ³ 0.

Задача 6. Какие из перечисленных функций являются характеристическими функциями случайных величин? Укажите распределения этих величин или объясните, почему функция не является характеристической:

а) φ(t) = sin (2t) ; б) φ(t) = 0.5cos3t + 0.5cos 2t ; в) φ(t) = exp(2it − 8t2 ).

Решение. а) Функция φ(t) = sin(2t) не является характеристической функцией случайной величины, так как ее значение в нуле отлично от 1.

б) Как известно, функция cos ax при любом вещественном a является характеристической функцией двухточечной симметричной случайной величины, принимающей с равными вероятностями значения a и −a (проверить!)

10